六年级下册数学教案-4.19 圆锥的体积 浙教版(表格式)
文档属性
| 名称 | 六年级下册数学教案-4.19 圆锥的体积 浙教版(表格式) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-18 00:00:00 | ||
图片预览


文档简介
《圆锥的体积》教学设计
教学目标
1、结合具体情境和实践活动,通过分小组实验,使学生自主探索出圆锥体积与圆柱体积之间的关系,初步掌握圆锥体积的计算公式,并能运用公式正确地计算圆锥的体积,解决实际生活中有关圆锥体积计算的简单问题。
2、借助已有的生活和学习经验,在小组活动中培养学生的动手操作能力和自主探索能力。
3、经历探索过程,引导学生初步认识从“特殊”到“一般”的规律,将未知转化为已知,合理发展数学思维,渗透探索问题的思想与方法。
4、通过活动,实践操作,巧妙设置探索障碍,激发学生的自主探索意识,发展学生的空间观念。
教学重点
?掌握圆锥体积的计算公式
教学难点
?正确探索出圆锥体积和圆柱体积之间的关系
学情分析
1、学生已经认识和了解了圆锥的特点,能够计算圆柱的体积(在已知圆柱的高、底面积(或底面半径、底面直径、底面周长)时,能够计算圆柱的体积),能够求圆柱的底面积或高(在已知圆柱的体积、高时,能求圆柱的底面积;已知圆柱的体积、底面积(或底面半径、底面直径、底面周长),能求圆柱的高)。并且学生通过学习推导圆柱的表面积和体积的过程,掌握了一种转化的数学方法。
2、学生在日常生活中(比如在油铺里)见到过圆锥形的漏斗,知道漏斗能够盛液体。同时,当学生们学习了圆柱的体积之后,而且已经能够计算圆柱形容器的容积时,他们有一种想要计算圆锥形容器容积的学习欲望。
3、学生分组操作时,肯定能借助倒水的实验,亲身感受等底等高的圆柱与圆锥体积间的3倍关系,但是他们不易发现隐藏在实验中的“等底等高”的这一条件,这是实验过程中的一个盲点。另外,学生在已知圆锥的体积、高(或底面积、底面半径、底面直径、底面周长),求圆锥的底面积(或高)时,往往容易忘记圆锥的体积得需要乘以3。
4、学生们在学习了如何计算圆柱的体积和圆柱形容器的容积之后,有一种想要计算圆锥体积和圆锥形容器容积的强烈愿望。同时,通过学生分组动手操作、实验、验证的活动,可以激发学生的学习乐趣和探疑的欲望。而且,学生已经理解、并且知道通过转化的数学方法来求圆锥形容器的容积。
5.我的思考:我觉得通过反复地操作活动和实验以及在老师和A组同学的帮助下,B组、C组同学能够理解“等底等高的圆柱与圆锥体积间的3倍关系”。同时,B组、C组同学能够独立或在A组同学的帮助下计算出圆锥的体积。但是,B组、C组同学在已知圆锥的体积、高(或底面积、底面半径、底面直径、底面周长),求圆锥的底面积(或高)时,往往由于容易忘记圆锥的体积得需要乘以3,而计算出现错误。所以,在学习过程中,一方面严格要求学生真正理解圆锥体积公式的意义,另一方面继续安排A组同学“一对一”或“一对二”地帮助B组、C组同学解决学习过程中遇到的困难。
教学准备
等底等高的圆柱形和圆锥形教具,既不等底也不等高的圆柱形和圆锥形教具,水、水槽、量杯等
教????学????过????程
教学环节
教学活动
设计意图
导入-知识铺垫
首先,带领学生复习圆锥的特点,尤其是圆锥的高的概念、并理解圆柱的体积公式(圆柱的体积=底面积×高),然后呈现圆锥形的麦堆,引导学生思考如何计算圆锥的体积。
引导学生在理解圆柱体积公式的基础上,思考圆柱体积与圆锥体积之间的联系,
并思考如何计算圆锥的体积。由已知到未知,由抛出问题到激发解决问题的欲望
新授-引领指导
引导学生利用老师提供的实验器具和材料,自己探索圆柱和圆锥体积之间的关系。然后,请同学们说一说他们是怎么进行实验的,圆柱体积与圆锥体积之间的联系是什么。
1、小组实验
将全班同学分成18组,由A组的18名同学带领B组、C组的同学进行操作。每组先用等底等高的圆柱形和圆锥形教具实验,然后再用既不等底也不等高的圆柱形和圆锥形教具实验。
2、小组交流
(1)组织收集信息:
(2)引导整理信息:
(3)参与处理信息:
围绕3倍关系的情况讨论
3、诱导反思:
为什么第一次实验时圆柱形容器的容积是圆锥形容器的容积的3倍,而第二次实验却不是3倍呢?
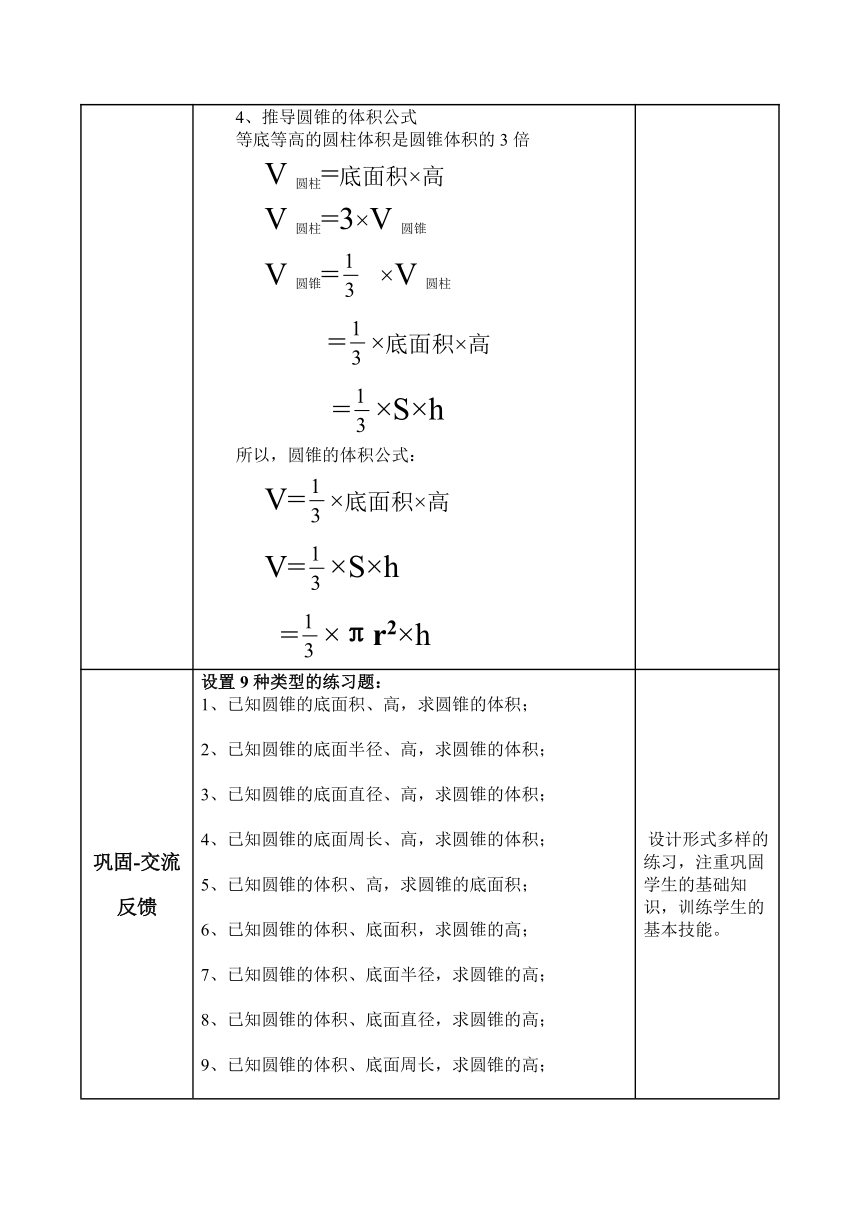
4、推导圆锥的体积公式
等底等高的圆柱体积是圆锥体积的3倍
V圆柱=底面积×高
V圆柱=3×V圆锥
V圆锥= ×V圆柱
=×底面积×高
=×S×h
所以,圆锥的体积公式:
V=×底面积×高
V=×S×h
=×πr2×h
?引导学生亲自动手操作、实验,让学生自主发现,在等底等高的情况下,圆柱的体积是圆锥体积的3倍。进而引导学生理解圆锥体积公式的推导过程和圆锥体积计算公式的意义。
巩固-交流反馈
设置9种类型的练习题:
已知圆锥的底面积、高,求圆锥的体积;
已知圆锥的底面半径、高,求圆锥的体积;
已知圆锥的底面直径、高,求圆锥的体积;
已知圆锥的底面周长、高,求圆锥的体积;
5、已知圆锥的体积、高,求圆锥的底面积;
6、已知圆锥的体积、底面积,求圆锥的高;
7、已知圆锥的体积、底面半径,求圆锥的高;
8、已知圆锥的体积、底面直径,求圆锥的高;
9、已知圆锥的体积、底面周长,求圆锥的高;
独立练习---反馈—交流---改正
?设计形式多样的练习,注重巩固学生的基础知识,训练学生的基本技能。
总结-归纳提升
9种类型练习题解法的总结、归纳:
已知圆锥的底面积、高,求圆锥的体积;
V=×S×h
代数:
已知圆锥的底面半径、高,求圆锥的体积;
V=×S×h
=×πr2×h
代数:
已知圆锥的底面直径、高,求圆锥的体积;
d=2r
r=d ÷2,
V=×S×h
=×πr2×h
代数:
已知圆锥的底面周长、高,求圆锥的体积;
C=2πr
r=C÷ (2π)
V=×S×h
=×πr2×h
代数:
5、已知圆锥的体积、高,求圆锥的底面积;
V=×S×h
×S×h = V
S×h=3V
S=3V÷h
代数:
6、已知圆锥的体积、底面积,求圆锥的高;
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
代数:
7、已知圆锥的体积、底面半径,求圆锥的高;
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
h =3V÷(πr2)
代数:
8、已知圆锥的体积、底面直径,求圆锥的高;
d=2r
r=d ÷2,
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
h =3V÷(πr2)
代数:
9、已知圆锥的体积、底面周长,求圆锥的高;
C=2πr
r=C÷ (2π)
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
h =3V÷(πr2)
代数:
通过这节课的学习,你们探索到了什么?是怎样推导出圆锥的体积公式的?
?教师引导,注重学生的自主归纳,让学生明白数学是可以操作的。同时,通过严格的计算教学,启发学生解决问题的思路,规范学生做题书写的格式,从而培养学生认真、严谨的数学学习习惯。
作业
教材第12页第2、3、4、5、6题;
教材第14页第10题;
?注重巩固学生的基础知识,训练学生的基本技能。
板书设计
等底等高的圆柱体积是圆锥体积的3倍
V圆柱=底面积×高
V圆柱=3×V圆锥
V圆锥= ×V圆柱
=×底面积×高
=×S×h
所以,圆锥的体积公式:
V=×底面积×高
V=×S×h
=×πr2×h
?
?
教学反思
本节课注重引导学生自主操作、实验,让学生自主发现等底等高的圆柱体积是圆锥体积的3倍,进而帮助学生理解圆锥体积的计算公式。同时,通过9种类型练习的训练、归纳和总结,巩固了学生的基础知识,训练了学生的基本技能,启发了学生的解题思路,并且也规范了他们的书写格式。让学生真切体会到,只要经过数学思路、格式的练习和训练,数学是可以被操作,也是可以被掌握的。让学生明白,任何人都可以学到适合他们自己的数学,任何人也都可以在数学上得到不同的发展。
教学目标
1、结合具体情境和实践活动,通过分小组实验,使学生自主探索出圆锥体积与圆柱体积之间的关系,初步掌握圆锥体积的计算公式,并能运用公式正确地计算圆锥的体积,解决实际生活中有关圆锥体积计算的简单问题。
2、借助已有的生活和学习经验,在小组活动中培养学生的动手操作能力和自主探索能力。
3、经历探索过程,引导学生初步认识从“特殊”到“一般”的规律,将未知转化为已知,合理发展数学思维,渗透探索问题的思想与方法。
4、通过活动,实践操作,巧妙设置探索障碍,激发学生的自主探索意识,发展学生的空间观念。
教学重点
?掌握圆锥体积的计算公式
教学难点
?正确探索出圆锥体积和圆柱体积之间的关系
学情分析
1、学生已经认识和了解了圆锥的特点,能够计算圆柱的体积(在已知圆柱的高、底面积(或底面半径、底面直径、底面周长)时,能够计算圆柱的体积),能够求圆柱的底面积或高(在已知圆柱的体积、高时,能求圆柱的底面积;已知圆柱的体积、底面积(或底面半径、底面直径、底面周长),能求圆柱的高)。并且学生通过学习推导圆柱的表面积和体积的过程,掌握了一种转化的数学方法。
2、学生在日常生活中(比如在油铺里)见到过圆锥形的漏斗,知道漏斗能够盛液体。同时,当学生们学习了圆柱的体积之后,而且已经能够计算圆柱形容器的容积时,他们有一种想要计算圆锥形容器容积的学习欲望。
3、学生分组操作时,肯定能借助倒水的实验,亲身感受等底等高的圆柱与圆锥体积间的3倍关系,但是他们不易发现隐藏在实验中的“等底等高”的这一条件,这是实验过程中的一个盲点。另外,学生在已知圆锥的体积、高(或底面积、底面半径、底面直径、底面周长),求圆锥的底面积(或高)时,往往容易忘记圆锥的体积得需要乘以3。
4、学生们在学习了如何计算圆柱的体积和圆柱形容器的容积之后,有一种想要计算圆锥体积和圆锥形容器容积的强烈愿望。同时,通过学生分组动手操作、实验、验证的活动,可以激发学生的学习乐趣和探疑的欲望。而且,学生已经理解、并且知道通过转化的数学方法来求圆锥形容器的容积。
5.我的思考:我觉得通过反复地操作活动和实验以及在老师和A组同学的帮助下,B组、C组同学能够理解“等底等高的圆柱与圆锥体积间的3倍关系”。同时,B组、C组同学能够独立或在A组同学的帮助下计算出圆锥的体积。但是,B组、C组同学在已知圆锥的体积、高(或底面积、底面半径、底面直径、底面周长),求圆锥的底面积(或高)时,往往由于容易忘记圆锥的体积得需要乘以3,而计算出现错误。所以,在学习过程中,一方面严格要求学生真正理解圆锥体积公式的意义,另一方面继续安排A组同学“一对一”或“一对二”地帮助B组、C组同学解决学习过程中遇到的困难。
教学准备
等底等高的圆柱形和圆锥形教具,既不等底也不等高的圆柱形和圆锥形教具,水、水槽、量杯等
教????学????过????程
教学环节
教学活动
设计意图
导入-知识铺垫
首先,带领学生复习圆锥的特点,尤其是圆锥的高的概念、并理解圆柱的体积公式(圆柱的体积=底面积×高),然后呈现圆锥形的麦堆,引导学生思考如何计算圆锥的体积。
引导学生在理解圆柱体积公式的基础上,思考圆柱体积与圆锥体积之间的联系,
并思考如何计算圆锥的体积。由已知到未知,由抛出问题到激发解决问题的欲望
新授-引领指导
引导学生利用老师提供的实验器具和材料,自己探索圆柱和圆锥体积之间的关系。然后,请同学们说一说他们是怎么进行实验的,圆柱体积与圆锥体积之间的联系是什么。
1、小组实验
将全班同学分成18组,由A组的18名同学带领B组、C组的同学进行操作。每组先用等底等高的圆柱形和圆锥形教具实验,然后再用既不等底也不等高的圆柱形和圆锥形教具实验。
2、小组交流
(1)组织收集信息:
(2)引导整理信息:
(3)参与处理信息:
围绕3倍关系的情况讨论
3、诱导反思:
为什么第一次实验时圆柱形容器的容积是圆锥形容器的容积的3倍,而第二次实验却不是3倍呢?
4、推导圆锥的体积公式
等底等高的圆柱体积是圆锥体积的3倍
V圆柱=底面积×高
V圆柱=3×V圆锥
V圆锥= ×V圆柱
=×底面积×高
=×S×h
所以,圆锥的体积公式:
V=×底面积×高
V=×S×h
=×πr2×h
?引导学生亲自动手操作、实验,让学生自主发现,在等底等高的情况下,圆柱的体积是圆锥体积的3倍。进而引导学生理解圆锥体积公式的推导过程和圆锥体积计算公式的意义。
巩固-交流反馈
设置9种类型的练习题:
已知圆锥的底面积、高,求圆锥的体积;
已知圆锥的底面半径、高,求圆锥的体积;
已知圆锥的底面直径、高,求圆锥的体积;
已知圆锥的底面周长、高,求圆锥的体积;
5、已知圆锥的体积、高,求圆锥的底面积;
6、已知圆锥的体积、底面积,求圆锥的高;
7、已知圆锥的体积、底面半径,求圆锥的高;
8、已知圆锥的体积、底面直径,求圆锥的高;
9、已知圆锥的体积、底面周长,求圆锥的高;
独立练习---反馈—交流---改正
?设计形式多样的练习,注重巩固学生的基础知识,训练学生的基本技能。
总结-归纳提升
9种类型练习题解法的总结、归纳:
已知圆锥的底面积、高,求圆锥的体积;
V=×S×h
代数:
已知圆锥的底面半径、高,求圆锥的体积;
V=×S×h
=×πr2×h
代数:
已知圆锥的底面直径、高,求圆锥的体积;
d=2r
r=d ÷2,
V=×S×h
=×πr2×h
代数:
已知圆锥的底面周长、高,求圆锥的体积;
C=2πr
r=C÷ (2π)
V=×S×h
=×πr2×h
代数:
5、已知圆锥的体积、高,求圆锥的底面积;
V=×S×h
×S×h = V
S×h=3V
S=3V÷h
代数:
6、已知圆锥的体积、底面积,求圆锥的高;
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
代数:
7、已知圆锥的体积、底面半径,求圆锥的高;
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
h =3V÷(πr2)
代数:
8、已知圆锥的体积、底面直径,求圆锥的高;
d=2r
r=d ÷2,
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
h =3V÷(πr2)
代数:
9、已知圆锥的体积、底面周长,求圆锥的高;
C=2πr
r=C÷ (2π)
V=×S×h
×S×h = V
S×h=3V
h =3V÷S
h =3V÷(πr2)
代数:
通过这节课的学习,你们探索到了什么?是怎样推导出圆锥的体积公式的?
?教师引导,注重学生的自主归纳,让学生明白数学是可以操作的。同时,通过严格的计算教学,启发学生解决问题的思路,规范学生做题书写的格式,从而培养学生认真、严谨的数学学习习惯。
作业
教材第12页第2、3、4、5、6题;
教材第14页第10题;
?注重巩固学生的基础知识,训练学生的基本技能。
板书设计
等底等高的圆柱体积是圆锥体积的3倍
V圆柱=底面积×高
V圆柱=3×V圆锥
V圆锥= ×V圆柱
=×底面积×高
=×S×h
所以,圆锥的体积公式:
V=×底面积×高
V=×S×h
=×πr2×h
?
?
教学反思
本节课注重引导学生自主操作、实验,让学生自主发现等底等高的圆柱体积是圆锥体积的3倍,进而帮助学生理解圆锥体积的计算公式。同时,通过9种类型练习的训练、归纳和总结,巩固了学生的基础知识,训练了学生的基本技能,启发了学生的解题思路,并且也规范了他们的书写格式。让学生真切体会到,只要经过数学思路、格式的练习和训练,数学是可以被操作,也是可以被掌握的。让学生明白,任何人都可以学到适合他们自己的数学,任何人也都可以在数学上得到不同的发展。
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
