人教版数学必修1 1.1.3 集合的基本运算(共15张ppt)
文档属性
| 名称 | 人教版数学必修1 1.1.3 集合的基本运算(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 247.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-18 16:22:45 | ||
图片预览





文档简介
课件15张PPT。——全集与补集 U是全班同学的集合,集合A是班上所有参加校运会同学的集合,集合B是班上所有没有参加校运动会同学的集合。
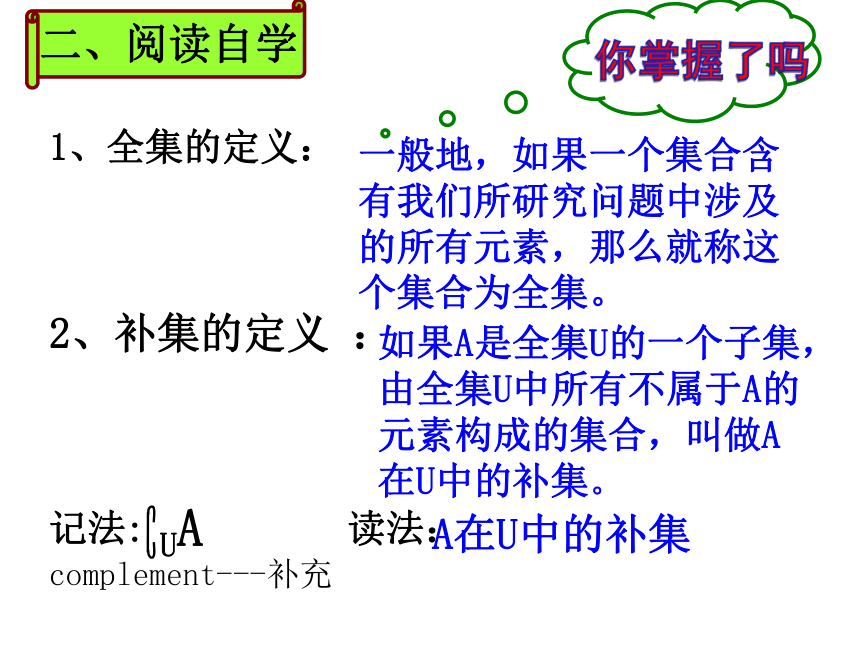
实例分析 集合B可以认为是由集合U中除去集合A中元素余下来的所有元素组成的集合。 二、阅读自学1、全集的定义:
?
2、补集的定义 :
记法: 读法:
complement---补充
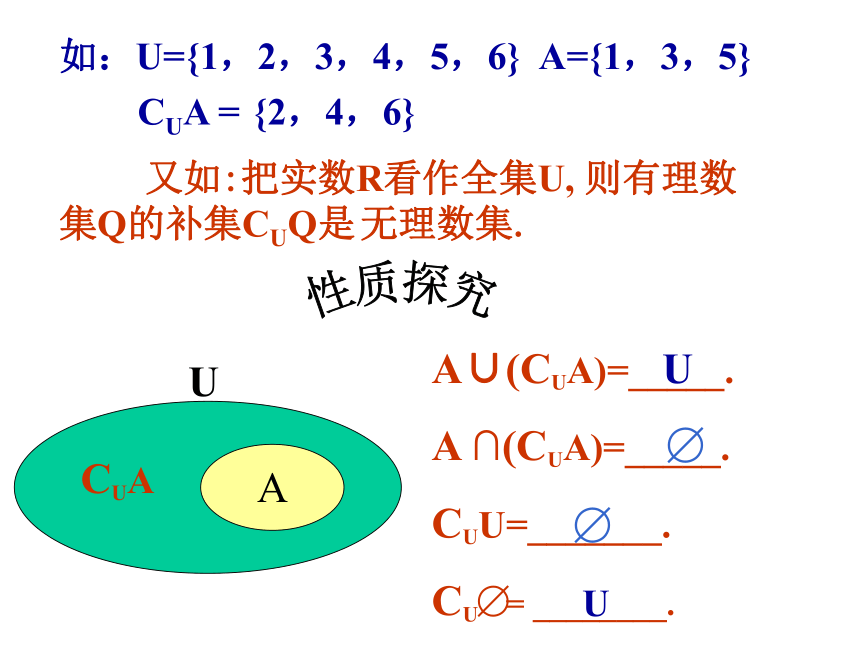
一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集。如果A是全集U的一个子集,由全集U中所有不属于A的元素构成的集合,叫做A在U中的补集。A在U中的补集如:U={1,2,3,4,5,6} A={1,3,5} 又如:把实数R看作全集U, 则有理数集Q的补集CUQ是 无理数集.性质探究U CUA =
{2,4,6}
U例题解析例1:试用集合A,B的交集、并集、补集分别表示图中Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分所表示的集合.
Ⅰ部分:__________
Ⅱ部分:__________
Ⅲ部分:__________
Ⅳ部分:__________或_________________.A∩BA∩ (CUB)B∩ (CUA)CU(A∪B) (CUA) ∩ (CUB) 例题解析例2:设全集为R,A={x|x<5},B={x|x>3}.求:
(1)A∩B; (2)A∪B; (3) CRA, CRB;
(4)(CRA) ∩ (CRB); (5) (CRA) ∪ (CRB);
(6) CR(A∩B); (7) CR(A ∪ B); 解(1) A∩B= {x|x<5} ∩ {x|x>3}={x|33}=R例2:设全集为R,A={x|x<5},B={x|x>3}.求:
(1)A∩B; (2)A∪B; (3) CRA, CRB;
(4)(CRA) ∩ (CRB); (5) (CRA) ∪ (CRB);
(6) CR(A.∩B); (7) CR(A ∪ B); (4)(CRA) ∩ (CRB)= {x|x≥5} ∩{x|x≤3} =(5)(CRA) ∪ (CRB)= {x|x≥5} ∪{x|x≤3}
={x|x≥5或x≤3}解:(3) CRA= {x|x≥5}, CRB= {x|x≤3} 例2:设全集为R,A={x|x<5},B={x|x>3}.求:
(1)A∩B; (2)A∪B; (3) CRA, CRB;
(4)(CRA) ∩ (CRB); (5) (CRA) ∪ (CRB);
(6) CR(A ∩ B); (7) CR(A ∪ B); 解(1) A∩B= {x|x<5} ∩ {x|x>3}={x|33}=R(6) CR(A ∩ B)={x|x≥5或x≤3}(7) CR(A ∪ B)=(4)(CRA) ∩ (CRB)= {x|x≥5} ∩{x|x≤3} =(5)(CRA) ∪ (CRB)= {x|x≥5} ∪{x|x≤3}
={x|x≥5或x≤3}(6) CR(A ∩ B)={x|x≥5或x≤3}(7) CR(A ∪ B)= 观察这些式子,你能发现什么结论?CR(A ∩ B)= (CRA) ∪ (CRB)
CR(A ∪ B)= (CRA) ∩ (CRB) 这是一个重要结论,有时候可以简化运算,不要求对这个结论进行严格证明._________.______________.4.已知全集U={1,2,3,4,5,6,7},A={2,4,5},
B={1,3,5,7}求A∩(CUB),(CUA)∩ (CUB).解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.若a≠1,且a≠4,a≠3,则A∪B={1,3,4,a},
A∩B= .若a=3,则A∪B={1,3,4} ,A∩B= ,5.设集合A={x|(x-3)(x-a)=0,a∈R},
B={x|(x-4)(x-1)=0},求A∪B,A∩B.解:由题意可知
B={1,4}, A={a,3},若a=1,则A∪B={1,3,4} ,A∩B={1}; 若a=4,则A∪B={1,3,4} ,A∩B={4}, 本节我们在集合的并、交两种基本运算的基础上学习了全集和补集的概念,在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示和理解集合的全集和补集以及并集、交集的综合运算.
实例分析 集合B可以认为是由集合U中除去集合A中元素余下来的所有元素组成的集合。 二、阅读自学1、全集的定义:
?
2、补集的定义 :
记法: 读法:
complement---补充
一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集。如果A是全集U的一个子集,由全集U中所有不属于A的元素构成的集合,叫做A在U中的补集。A在U中的补集如:U={1,2,3,4,5,6} A={1,3,5} 又如:把实数R看作全集U, 则有理数集Q的补集CUQ是 无理数集.性质探究U CUA =
{2,4,6}
U例题解析例1:试用集合A,B的交集、并集、补集分别表示图中Ⅰ,Ⅱ,Ⅲ,Ⅳ四个部分所表示的集合.
Ⅰ部分:__________
Ⅱ部分:__________
Ⅲ部分:__________
Ⅳ部分:__________或_________________.A∩BA∩ (CUB)B∩ (CUA)CU(A∪B) (CUA) ∩ (CUB) 例题解析例2:设全集为R,A={x|x<5},B={x|x>3}.求:
(1)A∩B; (2)A∪B; (3) CRA, CRB;
(4)(CRA) ∩ (CRB); (5) (CRA) ∪ (CRB);
(6) CR(A∩B); (7) CR(A ∪ B); 解(1) A∩B= {x|x<5} ∩ {x|x>3}={x|3
(1)A∩B; (2)A∪B; (3) CRA, CRB;
(4)(CRA) ∩ (CRB); (5) (CRA) ∪ (CRB);
(6) CR(A.∩B); (7) CR(A ∪ B); (4)(CRA) ∩ (CRB)= {x|x≥5} ∩{x|x≤3} =(5)(CRA) ∪ (CRB)= {x|x≥5} ∪{x|x≤3}
={x|x≥5或x≤3}解:(3) CRA= {x|x≥5}, CRB= {x|x≤3} 例2:设全集为R,A={x|x<5},B={x|x>3}.求:
(1)A∩B; (2)A∪B; (3) CRA, CRB;
(4)(CRA) ∩ (CRB); (5) (CRA) ∪ (CRB);
(6) CR(A ∩ B); (7) CR(A ∪ B); 解(1) A∩B= {x|x<5} ∩ {x|x>3}={x|3
={x|x≥5或x≤3}(6) CR(A ∩ B)={x|x≥5或x≤3}(7) CR(A ∪ B)= 观察这些式子,你能发现什么结论?CR(A ∩ B)= (CRA) ∪ (CRB)
CR(A ∪ B)= (CRA) ∩ (CRB) 这是一个重要结论,有时候可以简化运算,不要求对这个结论进行严格证明._________.______________.4.已知全集U={1,2,3,4,5,6,7},A={2,4,5},
B={1,3,5,7}求A∩(CUB),(CUA)∩ (CUB).解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.若a≠1,且a≠4,a≠3,则A∪B={1,3,4,a},
A∩B= .若a=3,则A∪B={1,3,4} ,A∩B= ,5.设集合A={x|(x-3)(x-a)=0,a∈R},
B={x|(x-4)(x-1)=0},求A∪B,A∩B.解:由题意可知
B={1,4}, A={a,3},若a=1,则A∪B={1,3,4} ,A∩B={1}; 若a=4,则A∪B={1,3,4} ,A∩B={4}, 本节我们在集合的并、交两种基本运算的基础上学习了全集和补集的概念,在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示和理解集合的全集和补集以及并集、交集的综合运算.
