人教版数学必修1 1.3.1 函数的单调性与最大(小)值(共19张ppt)
文档属性
| 名称 | 人教版数学必修1 1.3.1 函数的单调性与最大(小)值(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 798.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-18 00:00:00 | ||
图片预览


文档简介
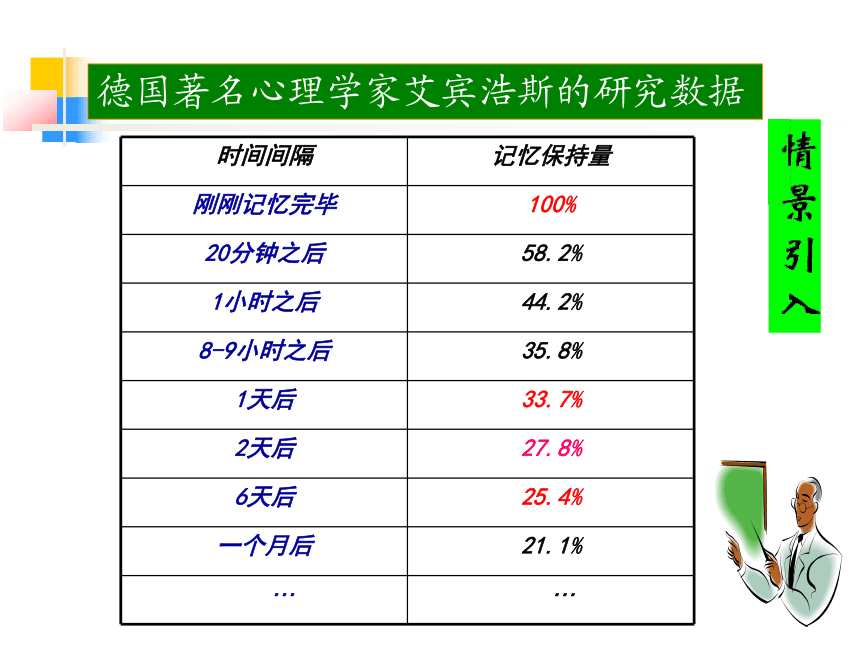
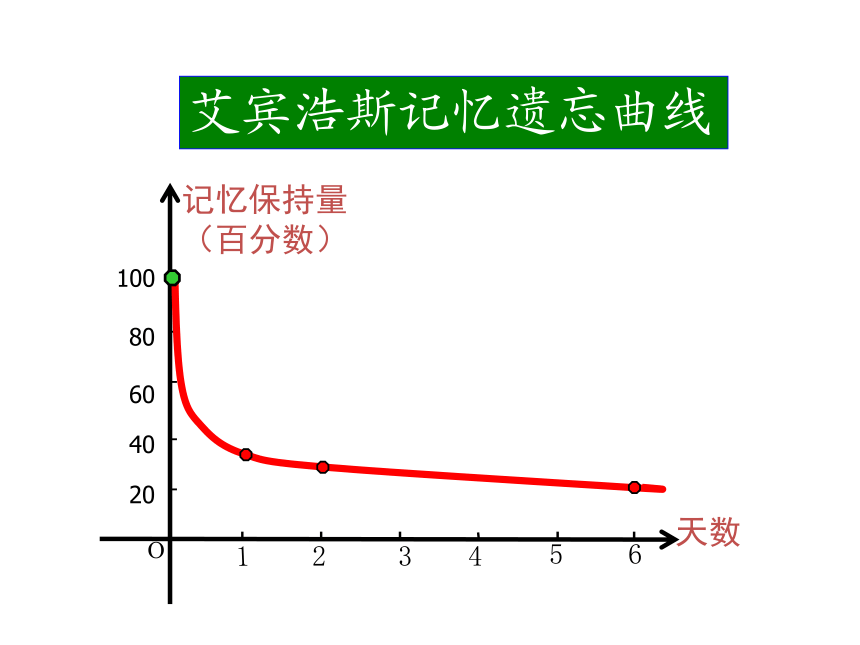
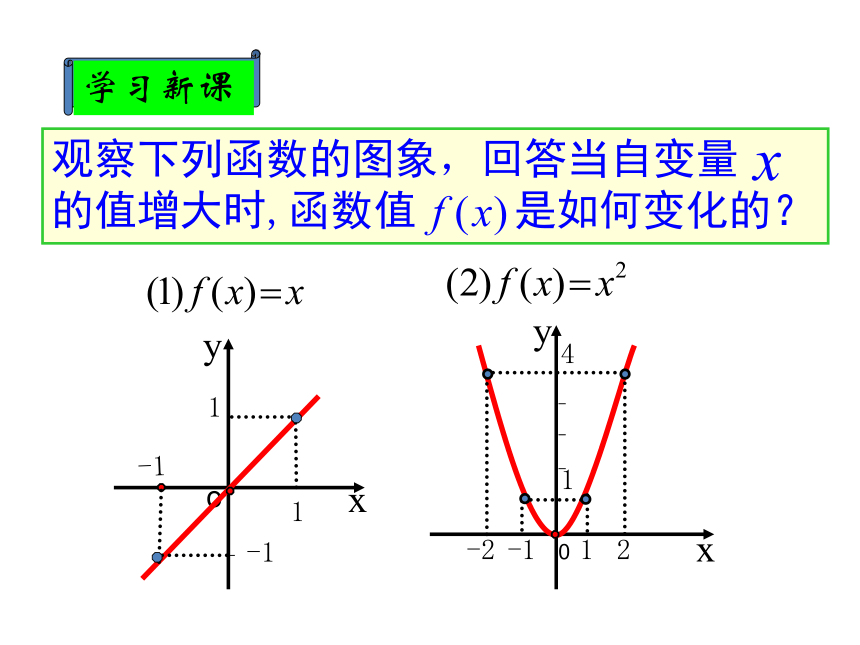
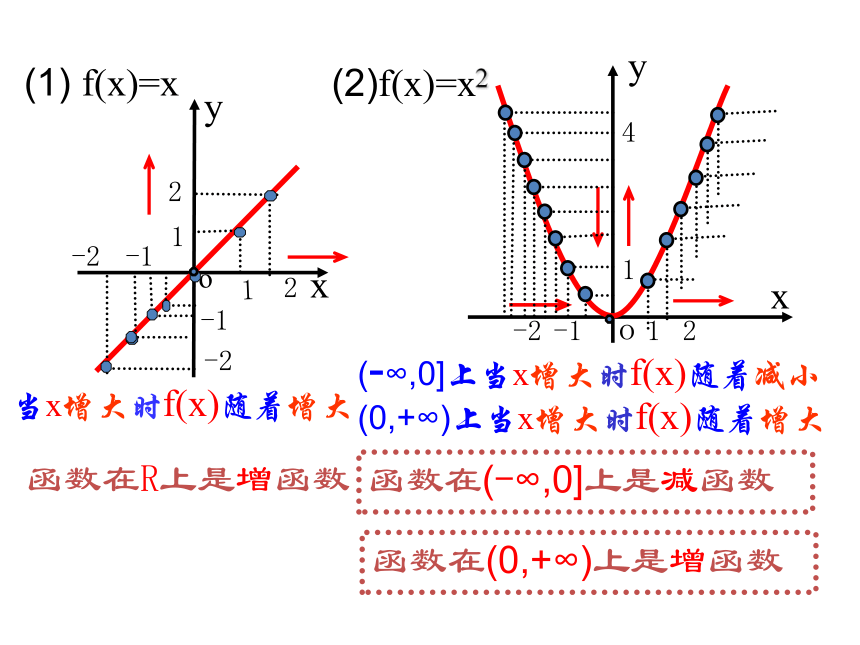
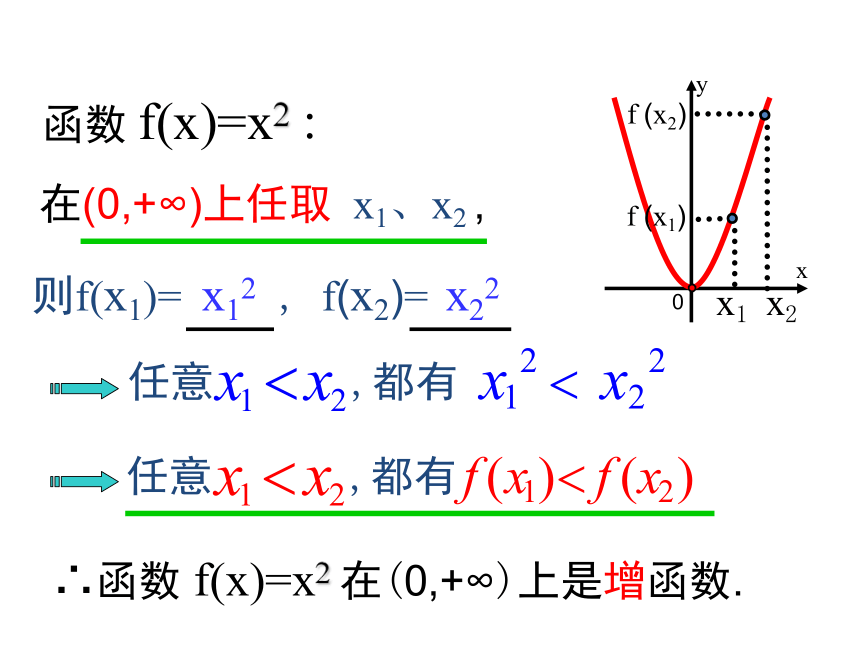
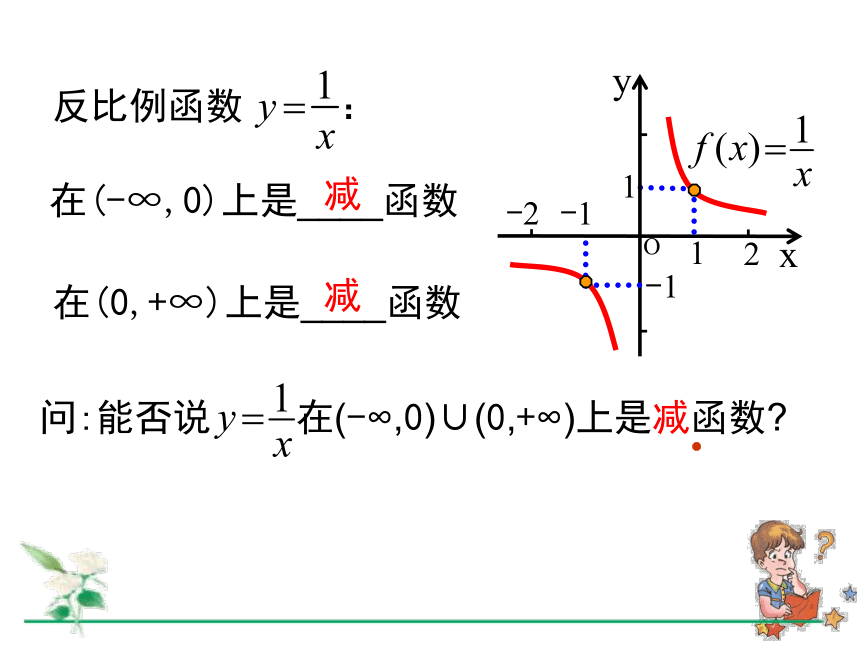
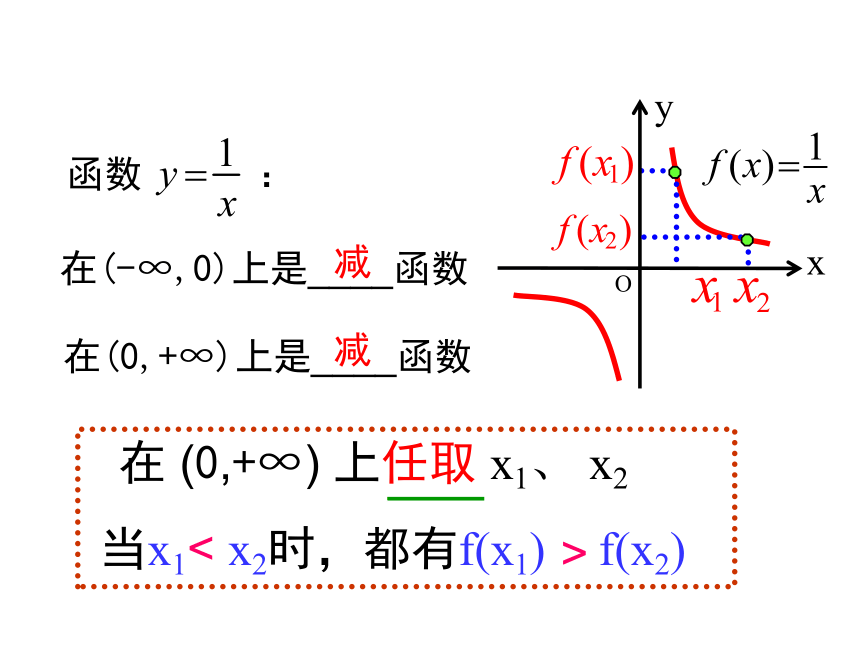
课件20张PPT。函数的单调性德国著名心理学家艾宾浩斯的研究数据 艾宾浩斯记忆遗忘曲线记忆保持量(百分数)天数O204060801003214561xyox观察下列函数的图象,回答当自变量 的值增大时,函数值 是如何变化的?0y1124-1-2-11-1(-∞,0]上当x增大时f(x)随着减小xyo-1xOy1124-1-21当x增大时f(x)随着增大函数在R上是增函数函数在(-∞,0]上是减函数(0,+∞)上当x增大时f(x)随着增大1函数在(0,+∞)上是增函数-2-1-222(1) f(x)=x (2)f(x)=x2 如果对于定义域I内某个区间D上的任意两个自变量的值 x1 、x2 ,当 x1<x2时,都有f(x1)<f(x2),那么就说函数f(x)在区间D上是增函数.一般地,设函数 f(x)的定义域为I:如果对于定义域I内某个区间D上的任意两个自变量的值 x1 、x2 ,当 x1<x2时,都有f(x1)>f(x2),那么就说函数f(x)在区间D上是减函数.如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间上具有(严格的)单调性,区间D叫做函数f(x)的单调区间.?函数 f(x)=x2 :x12x22x0x1x2yf (x1)f (x2)在(0,+∞)上任取 x1、x2 , 在(-∞,0)上是____函数在(0,+∞)上是____函数减减反比例函数 :-2yOx-11-112在(-∞,0)上是____函数在(0,+∞)上是____函数减减函数 :yOx 在 (0,+∞) 上任取 x1、 x2
当x1< x2时,都有f(x1) f(x2)>yOx-11-11 取自变量-1< 1,
而 f(-1) f(1)<探究:下列表述中
(1)f(a)(2)存在x1,x2∈[a,b],
当a≤x1(3)对任意x1,x2∈[a,b],
当a≤x1 可确定函数y=f(x)在区间[a,b]上为增函数的有______个
解:函数y=f(x)的单调区间有[-5,-2),[-2,1) ,[1,3), [3,5].例1. 如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数? 其中y=f(x)在区间[-2,1),[3,5]上是增函数;说明:孤立的点没有单调性,故区间端点处若有定义写开写闭均可.证明函数 在R上是减函数.例2.利用定义:4.下结论:由定义得出函数的单调性.1.设值:设任意x1、x2属于给定区间,且x1< x22.作差变形:作差f(x1)-f(x2)并适当变形;3.判断差符号:确定f(x1)-f(x2)的正负;证明函数单调性的步骤:[解题过程] f(x)=x2-2(a-1)x+3
=[x-(a-1)]2-(a-1)2+3,
∴此二次函数的对称轴为x=a-1.
∴f(x)的单调减区间为(-∞,a-1].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=a-1必须在直线x=4的右侧或与其重合.
∴a-1≥4,解得a≥5.3.(定义法)证明函数单调性的步骤:2.图象法判断函数的单调性:1. 增函数、减函数的定义;上升下降4.函数单调性的应用.如何确定函数的单调区间?思考题:
当x1< x2时,都有f(x1) f(x2)>yOx-11-11 取自变量-1< 1,
而 f(-1) f(1)<探究:下列表述中
(1)f(a)
当a≤x1
当a≤x1
解:函数y=f(x)的单调区间有[-5,-2),[-2,1) ,[1,3), [3,5].例1. 如图是定义在闭区间[-5,5]上的函数 y = f(x)的图象, 根据图象说出函数的单调区间, 以及在每一单调区间上, 函数是增函数还是减函数? 其中y=f(x)在区间[-2,1),[3,5]上是增函数;说明:孤立的点没有单调性,故区间端点处若有定义写开写闭均可.证明函数 在R上是减函数.例2.利用定义:4.下结论:由定义得出函数的单调性.1.设值:设任意x1、x2属于给定区间,且x1< x22.作差变形:作差f(x1)-f(x2)并适当变形;3.判断差符号:确定f(x1)-f(x2)的正负;证明函数单调性的步骤:[解题过程] f(x)=x2-2(a-1)x+3
=[x-(a-1)]2-(a-1)2+3,
∴此二次函数的对称轴为x=a-1.
∴f(x)的单调减区间为(-∞,a-1].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=a-1必须在直线x=4的右侧或与其重合.
∴a-1≥4,解得a≥5.3.(定义法)证明函数单调性的步骤:2.图象法判断函数的单调性:1. 增函数、减函数的定义;上升下降4.函数单调性的应用.如何确定函数的单调区间?思考题:
