人教版数学必修1 1.2 函数及其表示(复习课)(共29张ppt)
文档属性
| 名称 | 人教版数学必修1 1.2 函数及其表示(复习课)(共29张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 200.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-18 16:20:28 | ||
图片预览







文档简介
课件29张PPT。1.2复习课函数及其表示学习目标:
1.加深对函数概念的理解,加深对映射概念的了解. 2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.
3.理解简单的分段函数,并能简单应用.
重点:函数概念的理解,学会用集合与对应的语言刻画函数概念。
难点:函数符号y=f(x)太抽象学生不易接受知识回顾:1.函数的定义:其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值合{f(x)|x∈A}叫做函数的值域。设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数,记作
y=f(x),x∈A 2.函数的三要素: 3 .函数的表示法:4.分段函数
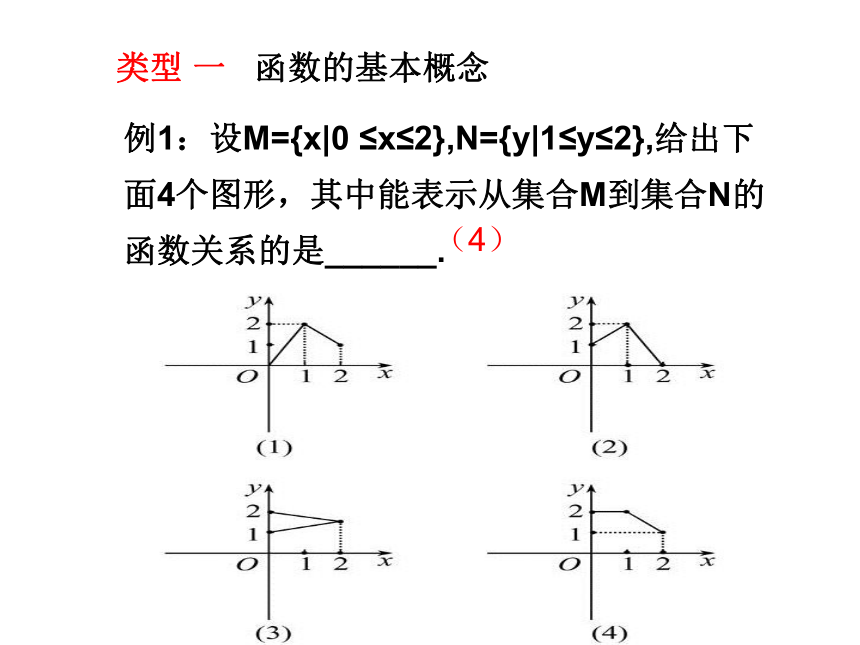
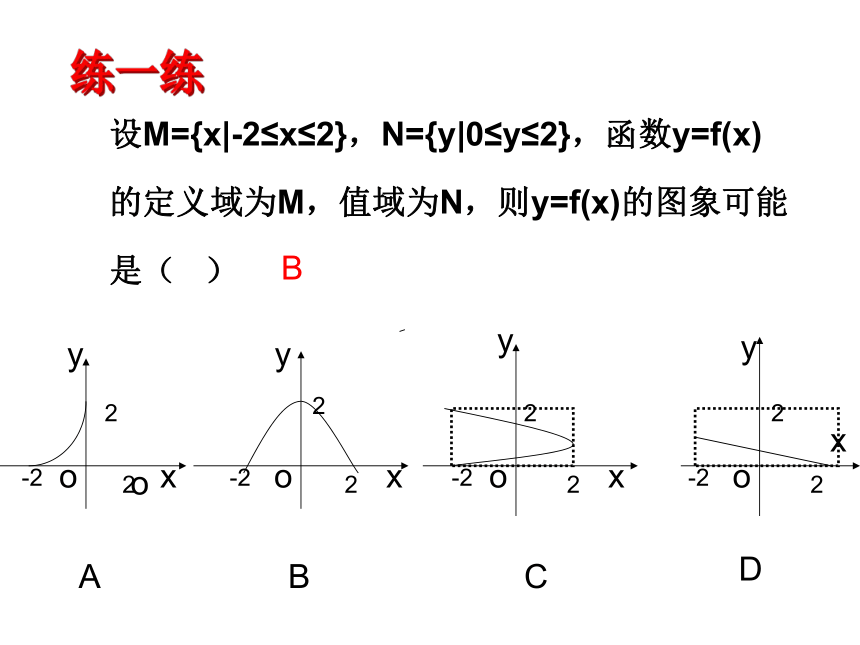
若函数在其定义域内,对于定义域内的不同取值 区间,有着不同的对应关系,这样的函数通常叫做分段函数.分段函数虽然由几部分组成,但它表示的是一个函数.分段函数的定义域是各段定义域的并集,值域是各段值域的并集知识回顾:定义域、值域和对应关系.解析法、图象法、列表法.注意了!类型 一 函数的基本概念 例1:设M={x|0 ≤x≤2},N={y|1≤y≤2},给出下面4个图形,其中能表示从集合M到集合N的函数关系的是______.(4)设M={x|-2≤x≤2},N={y|0≤y≤2},函数y=f(x)的定义域为M,值域为N,则y=f(x)的图象可能是( )练一练xB两个函数只要定义域和对应关系相同,两个函数就是相等函数。D如何判断两个函数是否相等?结论:类型 二 函数的定义域和函数值1.求函数定义域思路提示:思路展示:2.求函数值思路展示:议一议:周长为L的铁丝弯成下部为矩形,上部为半圆形的框架(如图所示),若矩形底边长为2x,求此框架围成图形的面积y与x的函数 解析式y=f(x),并求定义域。试一试 如何求实际问题中函数定义域思路展示:例5:某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
(其中x为不小于30的偶数)类型 三 函数的三种表示法在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x)
思路展示:练一练:思路展示:能力提升:思路展示:课堂小结:本节课主要复习了函数的定义、函数的三要素、函数的表示方法和分段函数。当堂检测:答案:函数概念的掌握,函数定义域、值域的求法,函数解析式的求法和图象的画法。解决问题:
1.加深对函数概念的理解,加深对映射概念的了解. 2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.
3.理解简单的分段函数,并能简单应用.
重点:函数概念的理解,学会用集合与对应的语言刻画函数概念。
难点:函数符号y=f(x)太抽象学生不易接受知识回顾:1.函数的定义:其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值合{f(x)|x∈A}叫做函数的值域。设A、B是非空数集,如果按照某种对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f: A→B为从集合A到集合B的一个函数,记作
y=f(x),x∈A 2.函数的三要素: 3 .函数的表示法:4.分段函数
若函数在其定义域内,对于定义域内的不同取值 区间,有着不同的对应关系,这样的函数通常叫做分段函数.分段函数虽然由几部分组成,但它表示的是一个函数.分段函数的定义域是各段定义域的并集,值域是各段值域的并集知识回顾:定义域、值域和对应关系.解析法、图象法、列表法.注意了!类型 一 函数的基本概念 例1:设M={x|0 ≤x≤2},N={y|1≤y≤2},给出下面4个图形,其中能表示从集合M到集合N的函数关系的是______.(4)设M={x|-2≤x≤2},N={y|0≤y≤2},函数y=f(x)的定义域为M,值域为N,则y=f(x)的图象可能是( )练一练xB两个函数只要定义域和对应关系相同,两个函数就是相等函数。D如何判断两个函数是否相等?结论:类型 二 函数的定义域和函数值1.求函数定义域思路提示:思路展示:2.求函数值思路展示:议一议:周长为L的铁丝弯成下部为矩形,上部为半圆形的框架(如图所示),若矩形底边长为2x,求此框架围成图形的面积y与x的函数 解析式y=f(x),并求定义域。试一试 如何求实际问题中函数定义域思路展示:例5:某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x元与日销售量y件之间有如下所表示的关系.
(其中x为不小于30的偶数)类型 三 函数的三种表示法在所给的坐标系中,如图,根据表格提供的数据描出实数对(x,y)的对应点,并确定y与x的一个函数关系式y=f(x)
思路展示:练一练:思路展示:能力提升:思路展示:课堂小结:本节课主要复习了函数的定义、函数的三要素、函数的表示方法和分段函数。当堂检测:答案:函数概念的掌握,函数定义域、值域的求法,函数解析式的求法和图象的画法。解决问题:
