第4章 图形的认识单元测试卷(基础卷+答案)
文档属性
| 名称 | 第4章 图形的认识单元测试卷(基础卷+答案) |  | |
| 格式 | zip | ||
| 文件大小 | 356.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-18 19:25:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
湘教版七年级上第4章图形的认识单元测试卷(基础卷)
时间:120分钟 满分:100分
姓名: 班级: 学号
选择题(每小题2分,共24分)
1、下列图形是平面图形的是( ?)
A.?球 B.?圆柱 C.?圆锥 D.?圆
下列语句中正确的是( ?)
A. 延长直线AB
B. 延长线段AB至C,使AC=BC
C. 延长射线OA
D. 延长线段AB至C,使BC=2AB
对于直线AB,线段CD,射线EF,在下列各图中能相交的是( ?)
A. B. C. D.
4、如图所示,从A地到B地有多条道路,人们会走中间的直路,而不会走其他的曲折的路,这是因为( )
A. 垂线段最短
B. 两点确定一条直线
C. 两点之间线段最短
D. 两直线相交,只有一个交点
能用∠α、∠AOB、∠O三种方式表示同一个角的图形是( )
A.? ?B. C.? D.?
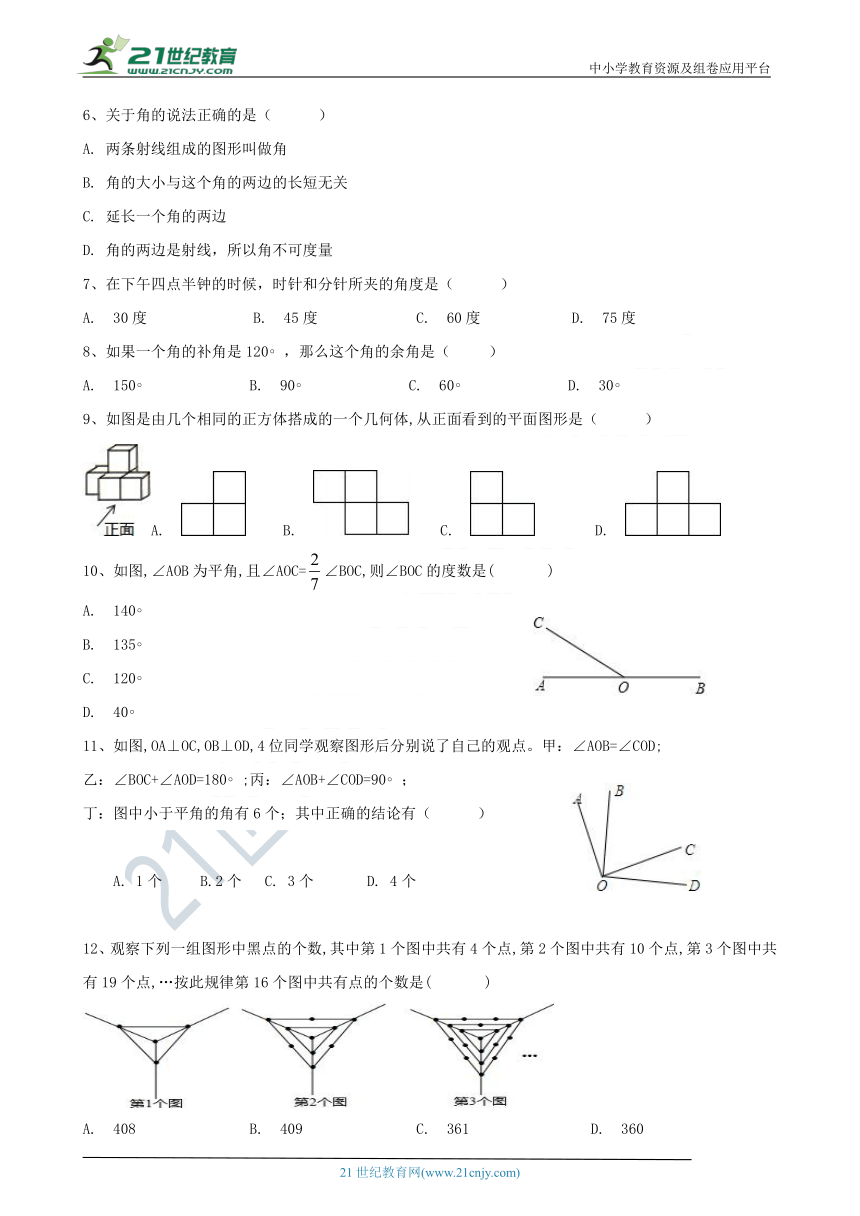
6、关于角的说法正确的是( ?)
A. 两条射线组成的图形叫做角
B. 角的大小与这个角的两边的长短无关
C. 延长一个角的两边
D. 角的两边是射线,所以角不可度量
7、在下午四点半钟的时候,时针和分针所夹的角度是(? )
A.?30度 B.?45度 C.?60度 D.?75度
8、如果一个角的补角是120?,那么这个角的余角是(? )
A.?150? B.?90? C.?60? D.?30?
9、如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( ?)
A.? B.? C.? D.?
10、如图,∠AOB为平角,且∠AOC=∠BOC,则∠BOC的度数是( )
A.?140?
B.?135?
C.?120?
D.?40?
11、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点。甲:∠AOB=∠COD;
乙:∠BOC+∠AOD=180?;丙:∠AOB+∠COD=90?;
丁:图中小于平角的角有6个;其中正确的结论有( ?)
A. 1个 B.2个 C. 3个 D. 4个
12、观察下列一组图形中黑点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…按此规律第16个图中共有点的个数是( )
A.?408 B.?409 C.?361 D.?360
填空题(每题3分,共18分)
计算:33°52′+21°54′=_______________
如图,图中有_________条射线,________条线段,这些线段是____________________
(14题)
15、如图,为抄近路践踏草坪是一种不文明的现象,
请你用数学知识解释出“人们喜欢抄近路”这一现象的原因是 (15题)
________________________________________________
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35?,那么∠2是___________度。
17、在一面墙上用一根钉子钉木条,木条总是来回晃动;用两根钉子钉木条,木条就会固定不动,用数学知识解释这种生活现象为______________________________________________________________
18、如图,∠1=15?,∠AOC=90?,点B.?O、D在同一直线上,则∠2的度数为________________________
(16题) (18题)
三、解答题(共58分)
19、计算(每题3分,共6分)
32°45′48″+20°25′ (2)179°48′-103°52′54″
(8分) 己知:四点A. B. C.?D的位置如图所示,
根据下列语句,画出图形。
(1)画直线AD、直线BC相交于点O;
(2)画射线AB.
21、(6分)如图:∠AOB=114?,OF是∠AOB的平分线,∠1和∠2互余,求∠1的度数。
22、(8分)如图,直线AB,CD相交于点O,OA平分∠EOC,若∠EOC=70?.
(1)求∠BOD的度数;
(2)求∠BOC的度数。
23、(8分)如图,已知∠AOC为直角,OC是∠BOD的平分线,且∠AOB=40?,求∠AOD的度数。
24、(10分)(1)已知一个角的余角是这个角的补角的,求出这个角以及这个角的余角和补角。
(2)如图,已知直线AB和CD相交于O点,CO⊥OE,OF平分∠AOE,∠COF=26?,求∠BOD的度数。
25、(12分)如图,点C为线段AD上一点,点B为CD的中点,且AD=13cm,BC=3cm.
(1)图中共有___________条线段;
(2)求AC的长;
(3)若点E在直线AD上,且EA=4cm,求BE的长。
参考答案
D 2、D 3、B 4、C 5、B 6、B. 7、B 8、D 9、D 10、A 11、C 12、B
13、55°46′ 14、8 6 AB AC AD BC BD CD 15、两点之间线段最短 16、55?
17、 两点确定一条直线. 18、105?
19、(1)53°10′48″ (2)75°55′6″
20、如图所示: 21、解:∵OF是∠AOB的平分线,∴∠AOF=∠FOB,
∵∠AOB=114?,∴∠AOF=12∠AOB=12×114?=57?即∠2=57?,
又∵∠1和∠2互余,∴∠1+∠2=90?,∴∠1=90??∠2=90??57?=33?
22、解:(1)∵OA平分∠EOC,∠EOC=70?,∴∠AOC=12∠EOC=35?, ∴∠BOD=∠AOC=35?;
(2)∵∠BOD+∠BOC=180?,∴∠BOC=180??35?=145?.
23、因为∠BOC=∠AOC?∠AOB=90??40?=50?
又OC平分∠BOD,所以∠COD=∠BOC=50?,所以∠AOD=∠AOC+∠COD=90?+50?=140?
24、解:(1)设这个角为x度,则这个角的余角是(90?x)度,补角是(180?x)度,
由题意得:90?x=14(180?x),
解得x=60, 所以,这个角是60?,这个角的余角是30?,这个角的补角是120?;
(2)∵CO⊥OE,∴∠COE=90?,
又∵∠COF=26?,∠EOF=90??26?=64?,
∵OF平分∠AOE,∴∠AOF=EOF=64?,∴∠AOC=64??26?=38?,
∵∠AOC与∠BOD是对顶角,∴∠BOD=38?.
25、解:(1)图中的线段有AC、AB、AD、CB、CD、BD这6条,故答案为:6;
(2)∵点B为CD的中点、BC=3cm,∴CD=2BC=6cm,
∵AD=13cm,∴AC=AD?CD=13?6=7(cm).
(3)如图1,当点E在AC上时,
∵AB=AC+BC=10cm、EA=4cm,∴BE=AB?AE=10?4=6(cm);
如图2,当点E在CA延长线上时,
∵AB=10cm、AE=4cm,∴BE=AE+AB=14cm;
综上,BE的长为6cm或14cm。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
