A典演练 北师大数学八上第七章第50课时 平行线的判定 习题课件
文档属性
| 名称 | A典演练 北师大数学八上第七章第50课时 平行线的判定 习题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-20 11:20:35 | ||
图片预览


文档简介
课件12张PPT。第七章? ? 平行线的证明?第 50 课时 平行线的判定北师大版 八年级上册考点 两直线平行的判定条件针对训练·各个击破1.利用如图所示的方法可以过直线外一点画已知直线的平行线,其依据
是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.对顶角相等,两直线平行
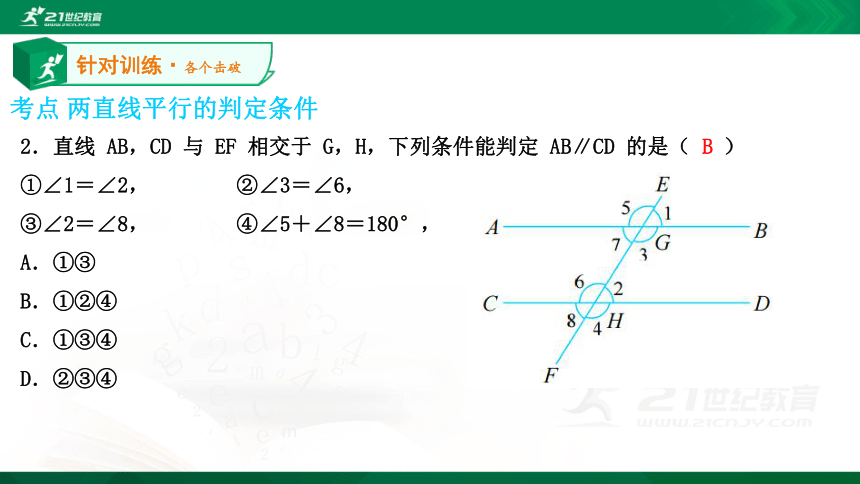
D.同旁内角互补,两直线平行A 考点 两直线平行的判定条件针对训练·各个击破2.直线 AB,CD 与 EF 相交于 G,H,下列条件能判定 AB∥CD 的是( )
①∠1=∠2, ②∠3=∠6,
③∠2=∠8, ④∠5+∠8=180°,
A.①③
B.①②④
C.①③④
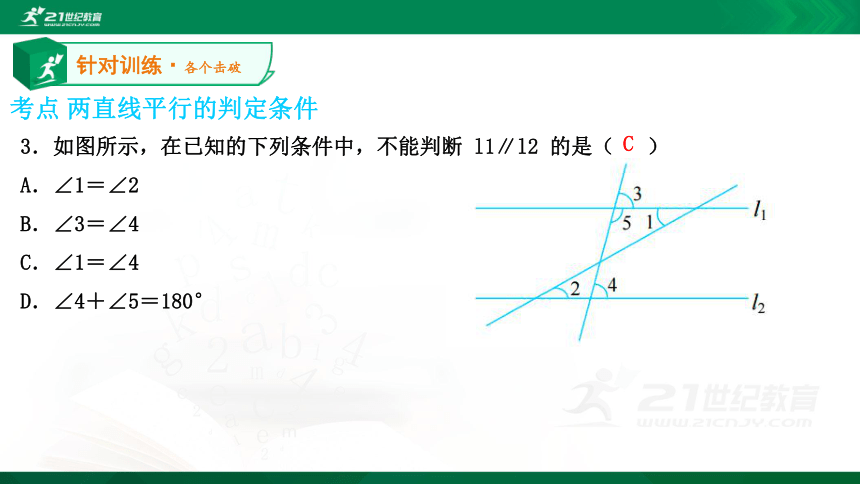
D.②③④B考点 两直线平行的判定条件针对训练·各个击破3.如图所示,在已知的下列条件中,不能判断 l1∥l2 的是( )
A.∠1=∠2
B.∠3=∠4
C.∠1=∠4
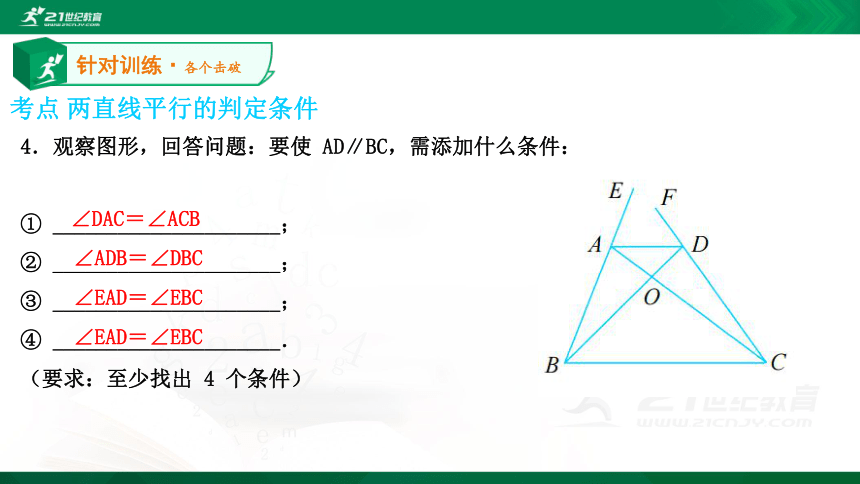
D.∠4+∠5=180° C考点 两直线平行的判定条件针对训练·各个击破4.观察图形,回答问题:要使 AD∥BC,需添加什么条件:
① _____________________;
② _____________________;
③ _____________________;
④ _____________________.
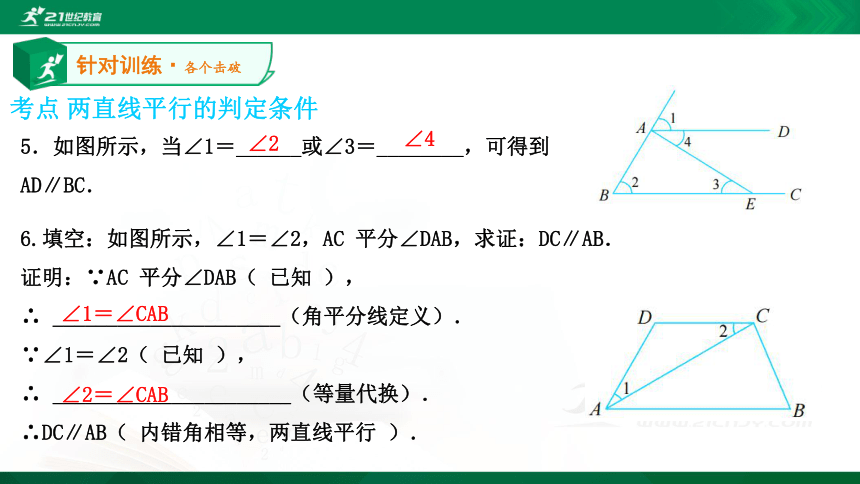
(要求:至少找出 4 个条件)∠DAC=∠ACB ∠ADB=∠DBC ∠EAD=∠EBC ∠EAD=∠EBC 考点 两直线平行的判定条件针对训练·各个击破5.如图所示,当∠1=______或∠3=________,可得到 AD∥BC.∠2∠46.填空:如图所示,∠1=∠2,AC 平分∠DAB,求证:DC∥AB.
证明:∵AC 平分∠DAB( 已知 ),
∴ _____________________(角平分线定义).
∵∠1=∠2( 已知 ),
∴ ______________________(等量代换).
∴DC∥AB( 内错角相等,两直线平行 ).∠1=∠CAB ∠2=∠CAB
巩固提升·融会贯通7.如图所示,∠1 和∠D 互余,CE⊥DE,问 AB 与 CD 平行吗?为什么?【答案】∵CE⊥DE,∴∠CED=90°.
∵∠1+∠CED+∠2=180°,
∴∠1+∠2=90°.
∵∠1 与∠D 互余,∴∠1+∠D=90°.
∴∠2=∠D,
∴AB∥CD(内错角相等,两直线平行).
巩固提升·融会贯通8.如图所示,已知直线 l1,l2,l3 被直线 l 所截,∠1=72°,∠2=108°,∠3
=72°,求证:l1∥l2∥l3.【答案】∵∠1=∠3=72°,
∴l1∥l3(内错角相等,两直线平行).
∵∠2=108°,
∴∠2+∠3=108°+72°=180°.
∴l2∥l3(同旁内角互补,两直线平行).
∴l1∥l2∥l3(平行于同一条直线的两条直线平行).
巩固提升·融会贯通9.如图所示,在△ABC 中,已知∠C=45°,∠ADB=90°,DE 为∠ADB 的平
分线,DE 与 CA 平行吗?说明你的理由.?
巩固提升·融会贯通10.如图所示,已知:EG,FG 分别平分∠BEF 和∠DFE,EG⊥FG.求证:AB∥CD.【答案】∵EG⊥FG(已知),
∴∠G=90°(垂直的定义).
在 Rt△EFG 中,
∠1+∠2=180°-∠G=90°(三角形内角和定理).
又∵∠BEF=2∠1,∠EFD=2∠2(角平分线的定义),
∴∠BEF+∠EFD=2∠1+2∠2=2(∠1+∠2)
=2×90°=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.对顶角相等,两直线平行
D.同旁内角互补,两直线平行A 考点 两直线平行的判定条件针对训练·各个击破2.直线 AB,CD 与 EF 相交于 G,H,下列条件能判定 AB∥CD 的是( )
①∠1=∠2, ②∠3=∠6,
③∠2=∠8, ④∠5+∠8=180°,
A.①③
B.①②④
C.①③④
D.②③④B考点 两直线平行的判定条件针对训练·各个击破3.如图所示,在已知的下列条件中,不能判断 l1∥l2 的是( )
A.∠1=∠2
B.∠3=∠4
C.∠1=∠4
D.∠4+∠5=180° C考点 两直线平行的判定条件针对训练·各个击破4.观察图形,回答问题:要使 AD∥BC,需添加什么条件:
① _____________________;
② _____________________;
③ _____________________;
④ _____________________.
(要求:至少找出 4 个条件)∠DAC=∠ACB ∠ADB=∠DBC ∠EAD=∠EBC ∠EAD=∠EBC 考点 两直线平行的判定条件针对训练·各个击破5.如图所示,当∠1=______或∠3=________,可得到 AD∥BC.∠2∠46.填空:如图所示,∠1=∠2,AC 平分∠DAB,求证:DC∥AB.
证明:∵AC 平分∠DAB( 已知 ),
∴ _____________________(角平分线定义).
∵∠1=∠2( 已知 ),
∴ ______________________(等量代换).
∴DC∥AB( 内错角相等,两直线平行 ).∠1=∠CAB ∠2=∠CAB
巩固提升·融会贯通7.如图所示,∠1 和∠D 互余,CE⊥DE,问 AB 与 CD 平行吗?为什么?【答案】∵CE⊥DE,∴∠CED=90°.
∵∠1+∠CED+∠2=180°,
∴∠1+∠2=90°.
∵∠1 与∠D 互余,∴∠1+∠D=90°.
∴∠2=∠D,
∴AB∥CD(内错角相等,两直线平行).
巩固提升·融会贯通8.如图所示,已知直线 l1,l2,l3 被直线 l 所截,∠1=72°,∠2=108°,∠3
=72°,求证:l1∥l2∥l3.【答案】∵∠1=∠3=72°,
∴l1∥l3(内错角相等,两直线平行).
∵∠2=108°,
∴∠2+∠3=108°+72°=180°.
∴l2∥l3(同旁内角互补,两直线平行).
∴l1∥l2∥l3(平行于同一条直线的两条直线平行).
巩固提升·融会贯通9.如图所示,在△ABC 中,已知∠C=45°,∠ADB=90°,DE 为∠ADB 的平
分线,DE 与 CA 平行吗?说明你的理由.?
巩固提升·融会贯通10.如图所示,已知:EG,FG 分别平分∠BEF 和∠DFE,EG⊥FG.求证:AB∥CD.【答案】∵EG⊥FG(已知),
∴∠G=90°(垂直的定义).
在 Rt△EFG 中,
∠1+∠2=180°-∠G=90°(三角形内角和定理).
又∵∠BEF=2∠1,∠EFD=2∠2(角平分线的定义),
∴∠BEF+∠EFD=2∠1+2∠2=2(∠1+∠2)
=2×90°=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
