第1章 计数原理章末总结试题
图片预览

文档简介
章末总结
知识点一 两个计数原理
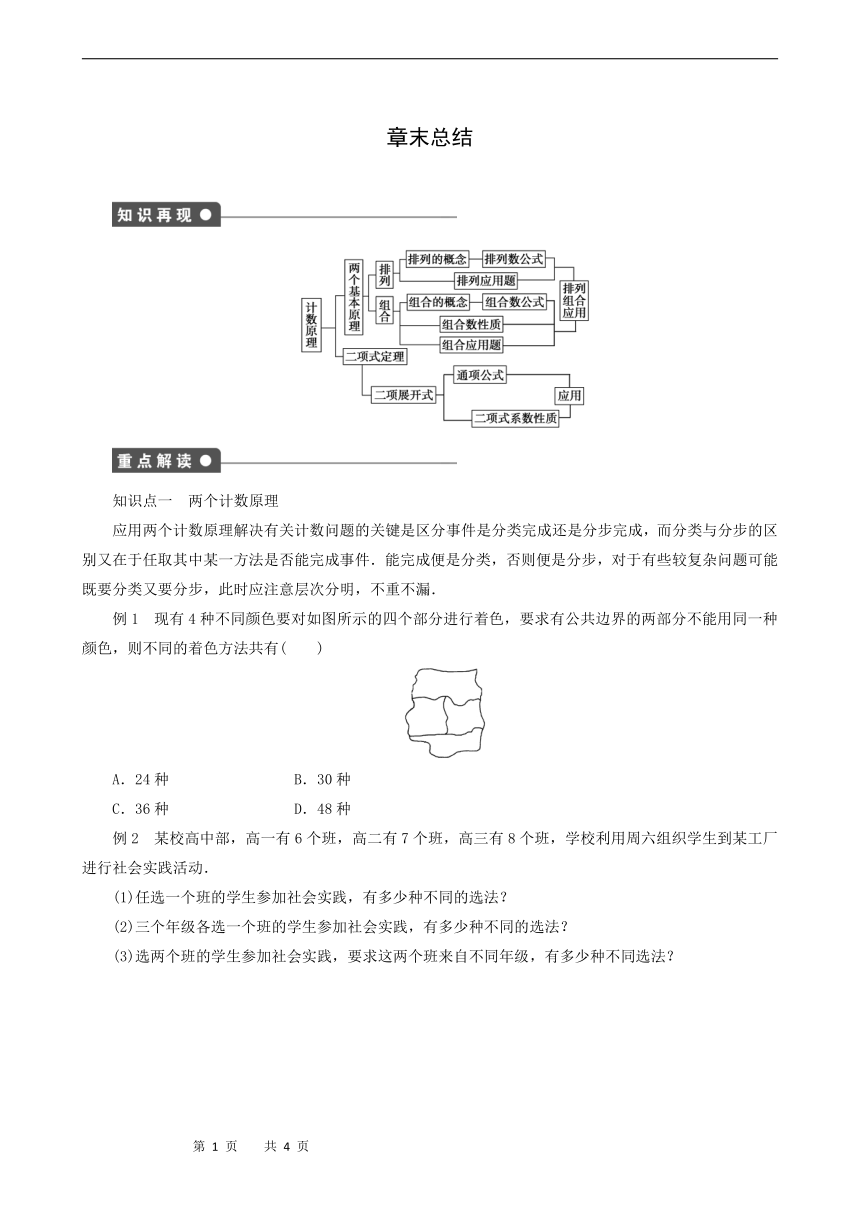
应用两个计数原理解决有关计数问题的关键是区分事件是分类完成还是分步完成,而分类与分步的区别又在于任取其中某一方法是否能完成事件.能完成便是分类,否则便是分步,对于有些较复杂问题可能既要分类又要分步,此时应注意层次分明,不重不漏.
例1 现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )
A.24种 B.30种
C.36种 D.48种
例2 某校高中部,高一有6个班,高二有7个班,高三有8个班,学校利用周六组织学生到某工厂进行社会实践活动.
(1)任选一个班的学生参加社会实践,有多少种不同的选法?
(2)三个年级各选一个班的学生参加社会实践,有多少种不同的选法?
(3)选两个班的学生参加社会实践,要求这两个班来自不同年级,有多少种不同选法?
知识点二 排列组合应用题
解排列组合应用题的关键在于区别它是排列问题,还是组合问题,也就是看它有无“顺序”.
解答排列组合应用题还应善于运用转化思想,把一些问题与排列组合基本类型相联系,从而把这些问题转化为基本类型,然后加以解决.
例3 有四名男生和三名女生排成一排,按下列要求各有多少种不同的排法?
(1)男甲排在正中间;
(2)男甲不在排头,女乙不在排尾.
例4 用1,2,3,4,5,6,7,8组成没有重复数字的八位数,要求1与2相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有多少个?
知识点三 二项式定理及应用
二项式定理的重点是二项展开式及通项公式的联系和应用.二项展开式的通项公式是解决与二项式定理有关问题的基础;二项展开式的性质是解题的关键;利用二项展开式可以证明整除性问题,讨论项的有关性质,证明组合数恒等式,进行近似计算等.赋值法与待定系数法是解决二项式定理相关问题常用的方法.
例5 二项式(2+x)n的展开式中,前三项的系数依次成等差数列,则展开式的第8项的系数为________.(用数字表示)
例6 已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+a3+…+a11=________.
例7 求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
章末总结
答案
重点解读
例1 D [将原图从上而下4部分区域标为1,2,3,4.因为1,2,3之间不能同色,1与4可以同色,因此,要分类讨论1,4同色与不同色两种情况,则不同的着色方法种数为4×3×2+4×3×2×1=48.故选D.]
例2 解 (1)分三类:第一类从高一年级选一个班,有6种不同方法,第二类从高二年级选一个班,有7种不同方法,第三类从高三年级选一个班,有8种不同方法,由分类加法计数原理,共有6+7+8=21(种)不同选法.
(2)分三步:第一步从高一年级选一个班,有6种不同的方法;第二步从高二年级选一个班,有7种不同的方法;第三步从高三年级选一个班,有8种不同的方法,由分步乘法计数原理,共有6×7×8=336(种)不同的选法.
(3)分三类,每类又分两步,第一类要从高一、高二两个年级各选一个班,有6×7种不同方法;第二类从高一、高三两个年级各选一个班,有6×8种不同方法;第三类从高二、高三两个年级各选一个班,有7×8种不同方法,故共有6×7+6×8+7×8=146(种)不同选法.
例3 解 (1)男甲排在正中间位置,其他六人排在余下的六个位置上,共有A=720(种)不同的排法.
(2)分四类考虑(特殊元素法):
①男甲不在排头,女乙不在排尾,男甲也不在排尾,女乙也不在排头(即男甲、女乙在中间5个位置上),有AA种排法;
②女乙在排头男甲不在排尾,有AA种排法;
③男甲在排尾女乙不在排头,有AA种排法;
④男甲在排尾且女乙在排头,共有A种排法.
根据分类加法计数原理,共有AA+2AA+A=3720(种)排法.
例4 解 将1、2,3、4,5、6看成3个整体,进行全排列有A种排法,3个整体间分别进行排列有A·A·A种方法.在由3个整体形成的4个空档中选出2个插入7、8两个数,共有A种方法,故共有A·A·A·A·A=576(种)排法.
例5 16
解析 第1项为2n,第2项为C2n-1x,第3项为C2n-2x2.∴2C·2n-1=2n+C2n-2.∴n=8.
∴T8=C2x7,其系数为2C=16.
例6 -65
解析 令x=0,得a0=1;
令x=1,得a0+a1+a2+…+a11=-64;
∴a1+a2+…+a11=-65.
例7 证明 因为1+3+32+…+33n-1
==(33n-1)=(27n-1)=[(26+1)n-1]
而(26+1)n-1=C26n+C26n-1+…+C26+C260-1=C26n+C26n-1+…+C26.
因为n为大于1的偶数,所以原式能被26整除.
知识点一 两个计数原理
应用两个计数原理解决有关计数问题的关键是区分事件是分类完成还是分步完成,而分类与分步的区别又在于任取其中某一方法是否能完成事件.能完成便是分类,否则便是分步,对于有些较复杂问题可能既要分类又要分步,此时应注意层次分明,不重不漏.
例1 现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )
A.24种 B.30种
C.36种 D.48种
例2 某校高中部,高一有6个班,高二有7个班,高三有8个班,学校利用周六组织学生到某工厂进行社会实践活动.
(1)任选一个班的学生参加社会实践,有多少种不同的选法?
(2)三个年级各选一个班的学生参加社会实践,有多少种不同的选法?
(3)选两个班的学生参加社会实践,要求这两个班来自不同年级,有多少种不同选法?
知识点二 排列组合应用题
解排列组合应用题的关键在于区别它是排列问题,还是组合问题,也就是看它有无“顺序”.
解答排列组合应用题还应善于运用转化思想,把一些问题与排列组合基本类型相联系,从而把这些问题转化为基本类型,然后加以解决.
例3 有四名男生和三名女生排成一排,按下列要求各有多少种不同的排法?
(1)男甲排在正中间;
(2)男甲不在排头,女乙不在排尾.
例4 用1,2,3,4,5,6,7,8组成没有重复数字的八位数,要求1与2相邻,3与4相邻,5与6相邻,而7与8不相邻,这样的八位数共有多少个?
知识点三 二项式定理及应用
二项式定理的重点是二项展开式及通项公式的联系和应用.二项展开式的通项公式是解决与二项式定理有关问题的基础;二项展开式的性质是解题的关键;利用二项展开式可以证明整除性问题,讨论项的有关性质,证明组合数恒等式,进行近似计算等.赋值法与待定系数法是解决二项式定理相关问题常用的方法.
例5 二项式(2+x)n的展开式中,前三项的系数依次成等差数列,则展开式的第8项的系数为________.(用数字表示)
例6 已知(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11,那么a1+a2+a3+…+a11=________.
例7 求证:1+3+32+…+33n-1能被26整除(n为大于1的偶数).
章末总结
答案
重点解读
例1 D [将原图从上而下4部分区域标为1,2,3,4.因为1,2,3之间不能同色,1与4可以同色,因此,要分类讨论1,4同色与不同色两种情况,则不同的着色方法种数为4×3×2+4×3×2×1=48.故选D.]
例2 解 (1)分三类:第一类从高一年级选一个班,有6种不同方法,第二类从高二年级选一个班,有7种不同方法,第三类从高三年级选一个班,有8种不同方法,由分类加法计数原理,共有6+7+8=21(种)不同选法.
(2)分三步:第一步从高一年级选一个班,有6种不同的方法;第二步从高二年级选一个班,有7种不同的方法;第三步从高三年级选一个班,有8种不同的方法,由分步乘法计数原理,共有6×7×8=336(种)不同的选法.
(3)分三类,每类又分两步,第一类要从高一、高二两个年级各选一个班,有6×7种不同方法;第二类从高一、高三两个年级各选一个班,有6×8种不同方法;第三类从高二、高三两个年级各选一个班,有7×8种不同方法,故共有6×7+6×8+7×8=146(种)不同选法.
例3 解 (1)男甲排在正中间位置,其他六人排在余下的六个位置上,共有A=720(种)不同的排法.
(2)分四类考虑(特殊元素法):
①男甲不在排头,女乙不在排尾,男甲也不在排尾,女乙也不在排头(即男甲、女乙在中间5个位置上),有AA种排法;
②女乙在排头男甲不在排尾,有AA种排法;
③男甲在排尾女乙不在排头,有AA种排法;
④男甲在排尾且女乙在排头,共有A种排法.
根据分类加法计数原理,共有AA+2AA+A=3720(种)排法.
例4 解 将1、2,3、4,5、6看成3个整体,进行全排列有A种排法,3个整体间分别进行排列有A·A·A种方法.在由3个整体形成的4个空档中选出2个插入7、8两个数,共有A种方法,故共有A·A·A·A·A=576(种)排法.
例5 16
解析 第1项为2n,第2项为C2n-1x,第3项为C2n-2x2.∴2C·2n-1=2n+C2n-2.∴n=8.
∴T8=C2x7,其系数为2C=16.
例6 -65
解析 令x=0,得a0=1;
令x=1,得a0+a1+a2+…+a11=-64;
∴a1+a2+…+a11=-65.
例7 证明 因为1+3+32+…+33n-1
==(33n-1)=(27n-1)=[(26+1)n-1]
而(26+1)n-1=C26n+C26n-1+…+C26+C260-1=C26n+C26n-1+…+C26.
因为n为大于1的偶数,所以原式能被26整除.
