高中数学 人教A版必修五课件 第3课时 不等式
文档属性
| 名称 | 高中数学 人教A版必修五课件 第3课时 不等式 |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-21 23:00:52 | ||
图片预览











文档简介
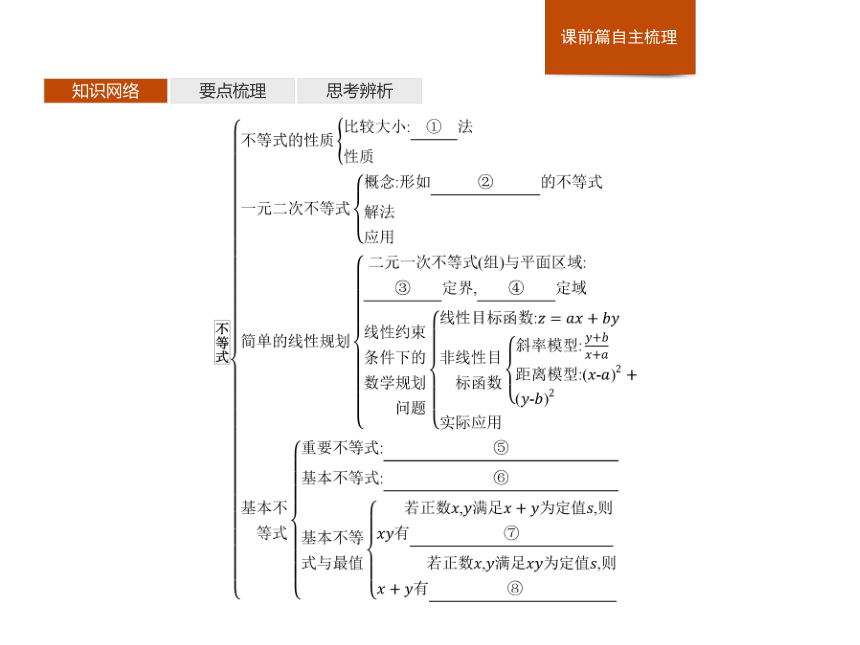
课件44张PPT。第3课时 不等式知识网络要点梳理思考辨析知识网络要点梳理思考辨析知识网络要点梳理思考辨析1.不等式的基本性质
(1)对称性:a>b?b(2)传递性:a>b,b>c?a>c.
(3)可加性:a>b?a+c>b+c.
(4)可乘性:a>b,c>0?ac>bc;a>b,c<0?ac(5)加法法则:a>b,c>d?a+c>b+d.
(6)乘法法则:a>b>0,c>d>0?ac>bd.
(7)乘方法则:a>b>0?an>bn(n∈N,n≥2).知识网络要点梳理思考辨析2.一元二次不等式的解法 知识网络要点梳理思考辨析3.一元二次不等式恒成立的条件 注意:在解决不等式ax2+bx+c>0(或≥0)对于一切x∈R恒成立问题时,当二次项系数含有字母时,需要对二次项系数a进行讨论,并研究当a=0时是否满足题意.知识网络要点梳理思考辨析4.二元一次不等式(组)表示的平面区域与线性规划问题
(1)二元一次不等式(组)表示的平面区域:直线定界,特殊点定域.
(2)线性规划问题:
求线性目标函数z=ax+by(ab≠0)的最值,当b>0时,直线过可行域且在y轴上的截距最大时,z值最大,在y轴上的截距最小时,z值最小;当b<0时,直线过可行域且在y轴上的截距最大时,z值最小,在y轴上的截距最小时,z值最大.
(3)线性约束条件下的非线性目标函数的最值问题:距离型:z=(x-a)2+(y-b)2,它表示可行域内的点(x,y)与点(a,b)之间距离的平方.结合可行域及目标函数表示的几何意义求最值即可.知识网络要点梳理思考辨析5.基本不等式及有关结论 且仅当a=b时,等号成立,即正数a与b的算术平均数不小于它们的几何平均数.
(2)重要不等式:若a∈R,b∈R,则a2+b2≥2ab,当且仅当a=b时,等号成立.
(3)几个常用的重要结论:知识网络要点梳理思考辨析6.利用基本不等式求最值
已知x>0,y>0,则注意:①求最值时要注意:“一正”“二定”“三相等”.所谓“一正”指正数,“二定”是指应用定理求最值时,和或积为定值,“三相等”是指等号成立.
②连续使用基本不等式时,注意等号要同时成立.知识网络要点梳理思考辨析判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.(2)若不等式a(x-2)(x+1)>0的解集是(-1,2),则a<0. ( )
(3)若a+c>b+d,则必有a>b,c>d. ( )
(4)关于x,y的不等式ax+by+c>0表示的平面区域是直线ax+by+c=0的上方. ( )
(5)若关于x的方程ax2+bx+c=0(a≠0)没有实数根,则关于x的不等式ax2+bx+c>0的解集为R. ( )答案:(1)× (2)√ (3)× (4)× (5)× (6)× 专题归纳高考体验专题一 不等式的性质及其应用 答案:C 专题归纳高考体验反思感悟判断关于不等式的命题真假的三种方法
1.直接运用不等式的性质:把要判断的命题和不等式的性质联系起来考虑,找到与命题相近的性质,然后进行推理判断.
2.利用函数的单调性:当利用不等式的性质不能比较大小时,可以利用指数函数、对数函数、幂函数的单调性等进行判断.
3.特殊值验证法:给要判断的几个式子中涉及的变量取一些特殊值,然后进行比较、判断.专题归纳高考体验变式训练1已知a>b,c>d,且c,d不为0,则下列不等式成立的是( )
A.ad>bc B.ac>bd
C.a-c>b-d D.a+c>b+d
解析:由不等式的性质易知选项D正确.
答案:D专题归纳高考体验专题二 一元二次不等式的解法及其应用
例2已知f(x)=-3x2+a(6-a)x+6.
(1)解关于a的不等式f(1)>0;
(2)若不等式f(x)>b的解集为(-1,3),求实数a,b的值;
(3)若不等式f(x)+a2x-12<0对一切x∈R恒成立,求实数a的取值范围.
分析:(1)利用一元二次不等式的一般解法求解;(2)根据一元二次不等式的解集与相应方程根的关系求解;(3)利用判别式求解.专题归纳高考体验专题归纳高考体验3.解含参数的一元二次不等式,可先考虑因式分解,再对根的大小进行分类讨论;若不能因式分解,则可对判别式进行分类讨论,分类要不重不漏.专题归纳高考体验变式训练2解关于x的不等式(m+3)x2+2mx+m-2>0(m∈R). 专题归纳高考体验专题归纳高考体验专题三 与线性规划有关的问题 专题归纳高考体验专题归纳高考体验专题归纳高考体验专题归纳高考体验反思感悟1.求目标函数的最值的一般步骤为:一作图、二平移、三求值.其关键是准确作出可行域,理解目标函数的意义.
2.常见的目标函数有:
(1)截距型:形如z=ax+by.求这类目标函数的最值时常将函数专题归纳高考体验专题归纳高考体验解析:先作出不等式组表示的平面区域,如图阴影部分所示.
要使阴影部分为直角三角形,且必有BC⊥AB.
因为x+y-4=0的斜率为-1,
所以直线kx-y=0的斜率为1,即k=1,故选A.
答案:A专题归纳高考体验专题四 基本不等式及其应用 专题归纳高考体验专题归纳高考体验反思感悟利用基本不等式求最值的方法
1.利用基本不等式解决条件最值的关键是构造和为定值或积为定值,主要有两种思路:
(1)对条件使用基本不等式,建立所求目标函数的不等式求解.
(2)条件变形,进行“1”的代换求目标函数的最值.
2.有些题目虽然不具备直接用基本不等式求最值的条件,但可以通过添项、分离常数、平方等手段使之能运用基本不等式.常用的方法还有:拆项法、变系数法、凑因子法、换元法、整体代换法等.专题归纳高考体验专题归纳高考体验考点一 不等式的性质
1.(2019·全国Ⅱ高考)若a>b,则( )
A.ln(a-b)>0 B.3a<3b
C.a3-b3>0 D.|a|>|b|
解析:取a=2,b=1,满足a>b.但ln(a-b)=0,排除A;
∵3a=9,3b=3,∴3a>3b,排除B;∵y=x3是增函数,a>b,∴a3>b3,故C正确;取a=1,b=-2,满足a>b,但|a|<|b|,排除D.故选C.
答案:C
2.(2017·北京高考)能够说明“设a,b,c是任意实数,若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为 .?
解析:答案不唯一,如令a=-1,b=-2,c=-3,则a>b>c,而a+b=-3=c,能够说明“设a,b,c是任意实数,若a>b>c,则a+b>c”是假命题.
答案:-1,-2,-3(答案不唯一)专题归纳高考体验考点二 不等式的解法
3.(2016·全国高考乙卷)设集合A={x|x2-4x+3<0},B={x|2x-3>0},则A∩B=( )答案:D 专题归纳高考体验4.(2019·天津高考)设x∈R,使不等式3x2+x-2<0成立的x的取值范围为 .?专题归纳高考体验考点三 线性规划问题 数z=-4x+y的最大值为 ( )
A.2 B.3 C.5 D.6解析:画出可行域如图,平移目标函数z=-4x+y可知过点A时取得最大值,得A(-1,1).
∴zmax=-4×(-1)+1=5.故选C.
答案:C专题归纳高考体验z=3x+2y的最大值是( )
A.-1 B.1 C.10 D.12
解析:在平面直角坐标系内画出题中的不等式组表示的平面区域为以(-1,1),(1,-1),(2,2)为顶点的三角形区域(包含边界),由图易得当直线z=3x+2y经过平面区域内的点(2,2)时,z=3x+2y取得最大值zmax=3×2+2×2=10.
答案:C专题归纳高考体验的最小值是( )
A.-15 B.-9 C.1 D.9
解析:画出不等式组所表示的平面区域如图所示,结合目标函数z=2x+y的几何意义,可得z在点B(-6,-3)处取得最小值,即zmin=-12-3=-15,故选A.答案:A 专题归纳高考体验z=3x-y的最大值是 .?
解析:画出可行域为图中阴影部分,z=3x-y表示直线3x-y-z=0的纵截距的相反数,当直线3x-y-z=0过点C(3,0)时,z取得最大值9.答案:9 专题归纳高考体验的最大值为 .?
解析:作出可行域,如图阴影部分所示(包括边界).答案:6 专题归纳高考体验答案:3 专题归纳高考体验11.(2016·全国高考乙卷)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.?专题归纳高考体验所以zmax=2 100×60+900×100=216 000.
答案:216 000专题归纳高考体验考点四 基本不等式 A.2 B.3 C.4 D.5 答案:C 专题归纳高考体验答案:C 专题归纳高考体验答案:B 专题归纳高考体验
(1)对称性:a>b?b
(3)可加性:a>b?a+c>b+c.
(4)可乘性:a>b,c>0?ac>bc;a>b,c<0?ac
(6)乘法法则:a>b>0,c>d>0?ac>bd.
(7)乘方法则:a>b>0?an>bn(n∈N,n≥2).知识网络要点梳理思考辨析2.一元二次不等式的解法 知识网络要点梳理思考辨析3.一元二次不等式恒成立的条件 注意:在解决不等式ax2+bx+c>0(或≥0)对于一切x∈R恒成立问题时,当二次项系数含有字母时,需要对二次项系数a进行讨论,并研究当a=0时是否满足题意.知识网络要点梳理思考辨析4.二元一次不等式(组)表示的平面区域与线性规划问题
(1)二元一次不等式(组)表示的平面区域:直线定界,特殊点定域.
(2)线性规划问题:
求线性目标函数z=ax+by(ab≠0)的最值,当b>0时,直线过可行域且在y轴上的截距最大时,z值最大,在y轴上的截距最小时,z值最小;当b<0时,直线过可行域且在y轴上的截距最大时,z值最小,在y轴上的截距最小时,z值最大.
(3)线性约束条件下的非线性目标函数的最值问题:距离型:z=(x-a)2+(y-b)2,它表示可行域内的点(x,y)与点(a,b)之间距离的平方.结合可行域及目标函数表示的几何意义求最值即可.知识网络要点梳理思考辨析5.基本不等式及有关结论 且仅当a=b时,等号成立,即正数a与b的算术平均数不小于它们的几何平均数.
(2)重要不等式:若a∈R,b∈R,则a2+b2≥2ab,当且仅当a=b时,等号成立.
(3)几个常用的重要结论:知识网络要点梳理思考辨析6.利用基本不等式求最值
已知x>0,y>0,则注意:①求最值时要注意:“一正”“二定”“三相等”.所谓“一正”指正数,“二定”是指应用定理求最值时,和或积为定值,“三相等”是指等号成立.
②连续使用基本不等式时,注意等号要同时成立.知识网络要点梳理思考辨析判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.(2)若不等式a(x-2)(x+1)>0的解集是(-1,2),则a<0. ( )
(3)若a+c>b+d,则必有a>b,c>d. ( )
(4)关于x,y的不等式ax+by+c>0表示的平面区域是直线ax+by+c=0的上方. ( )
(5)若关于x的方程ax2+bx+c=0(a≠0)没有实数根,则关于x的不等式ax2+bx+c>0的解集为R. ( )答案:(1)× (2)√ (3)× (4)× (5)× (6)× 专题归纳高考体验专题一 不等式的性质及其应用 答案:C 专题归纳高考体验反思感悟判断关于不等式的命题真假的三种方法
1.直接运用不等式的性质:把要判断的命题和不等式的性质联系起来考虑,找到与命题相近的性质,然后进行推理判断.
2.利用函数的单调性:当利用不等式的性质不能比较大小时,可以利用指数函数、对数函数、幂函数的单调性等进行判断.
3.特殊值验证法:给要判断的几个式子中涉及的变量取一些特殊值,然后进行比较、判断.专题归纳高考体验变式训练1已知a>b,c>d,且c,d不为0,则下列不等式成立的是( )
A.ad>bc B.ac>bd
C.a-c>b-d D.a+c>b+d
解析:由不等式的性质易知选项D正确.
答案:D专题归纳高考体验专题二 一元二次不等式的解法及其应用
例2已知f(x)=-3x2+a(6-a)x+6.
(1)解关于a的不等式f(1)>0;
(2)若不等式f(x)>b的解集为(-1,3),求实数a,b的值;
(3)若不等式f(x)+a2x-12<0对一切x∈R恒成立,求实数a的取值范围.
分析:(1)利用一元二次不等式的一般解法求解;(2)根据一元二次不等式的解集与相应方程根的关系求解;(3)利用判别式求解.专题归纳高考体验专题归纳高考体验3.解含参数的一元二次不等式,可先考虑因式分解,再对根的大小进行分类讨论;若不能因式分解,则可对判别式进行分类讨论,分类要不重不漏.专题归纳高考体验变式训练2解关于x的不等式(m+3)x2+2mx+m-2>0(m∈R). 专题归纳高考体验专题归纳高考体验专题三 与线性规划有关的问题 专题归纳高考体验专题归纳高考体验专题归纳高考体验专题归纳高考体验反思感悟1.求目标函数的最值的一般步骤为:一作图、二平移、三求值.其关键是准确作出可行域,理解目标函数的意义.
2.常见的目标函数有:
(1)截距型:形如z=ax+by.求这类目标函数的最值时常将函数专题归纳高考体验专题归纳高考体验解析:先作出不等式组表示的平面区域,如图阴影部分所示.
要使阴影部分为直角三角形,且必有BC⊥AB.
因为x+y-4=0的斜率为-1,
所以直线kx-y=0的斜率为1,即k=1,故选A.
答案:A专题归纳高考体验专题四 基本不等式及其应用 专题归纳高考体验专题归纳高考体验反思感悟利用基本不等式求最值的方法
1.利用基本不等式解决条件最值的关键是构造和为定值或积为定值,主要有两种思路:
(1)对条件使用基本不等式,建立所求目标函数的不等式求解.
(2)条件变形,进行“1”的代换求目标函数的最值.
2.有些题目虽然不具备直接用基本不等式求最值的条件,但可以通过添项、分离常数、平方等手段使之能运用基本不等式.常用的方法还有:拆项法、变系数法、凑因子法、换元法、整体代换法等.专题归纳高考体验专题归纳高考体验考点一 不等式的性质
1.(2019·全国Ⅱ高考)若a>b,则( )
A.ln(a-b)>0 B.3a<3b
C.a3-b3>0 D.|a|>|b|
解析:取a=2,b=1,满足a>b.但ln(a-b)=0,排除A;
∵3a=9,3b=3,∴3a>3b,排除B;∵y=x3是增函数,a>b,∴a3>b3,故C正确;取a=1,b=-2,满足a>b,但|a|<|b|,排除D.故选C.
答案:C
2.(2017·北京高考)能够说明“设a,b,c是任意实数,若a>b>c,则a+b>c”是假命题的一组整数a,b,c的值依次为 .?
解析:答案不唯一,如令a=-1,b=-2,c=-3,则a>b>c,而a+b=-3=c,能够说明“设a,b,c是任意实数,若a>b>c,则a+b>c”是假命题.
答案:-1,-2,-3(答案不唯一)专题归纳高考体验考点二 不等式的解法
3.(2016·全国高考乙卷)设集合A={x|x2-4x+3<0},B={x|2x-3>0},则A∩B=( )答案:D 专题归纳高考体验4.(2019·天津高考)设x∈R,使不等式3x2+x-2<0成立的x的取值范围为 .?专题归纳高考体验考点三 线性规划问题 数z=-4x+y的最大值为 ( )
A.2 B.3 C.5 D.6解析:画出可行域如图,平移目标函数z=-4x+y可知过点A时取得最大值,得A(-1,1).
∴zmax=-4×(-1)+1=5.故选C.
答案:C专题归纳高考体验z=3x+2y的最大值是( )
A.-1 B.1 C.10 D.12
解析:在平面直角坐标系内画出题中的不等式组表示的平面区域为以(-1,1),(1,-1),(2,2)为顶点的三角形区域(包含边界),由图易得当直线z=3x+2y经过平面区域内的点(2,2)时,z=3x+2y取得最大值zmax=3×2+2×2=10.
答案:C专题归纳高考体验的最小值是( )
A.-15 B.-9 C.1 D.9
解析:画出不等式组所表示的平面区域如图所示,结合目标函数z=2x+y的几何意义,可得z在点B(-6,-3)处取得最小值,即zmin=-12-3=-15,故选A.答案:A 专题归纳高考体验z=3x-y的最大值是 .?
解析:画出可行域为图中阴影部分,z=3x-y表示直线3x-y-z=0的纵截距的相反数,当直线3x-y-z=0过点C(3,0)时,z取得最大值9.答案:9 专题归纳高考体验的最大值为 .?
解析:作出可行域,如图阴影部分所示(包括边界).答案:6 专题归纳高考体验答案:3 专题归纳高考体验11.(2016·全国高考乙卷)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2 100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.?专题归纳高考体验所以zmax=2 100×60+900×100=216 000.
答案:216 000专题归纳高考体验考点四 基本不等式 A.2 B.3 C.4 D.5 答案:C 专题归纳高考体验答案:C 专题归纳高考体验答案:B 专题归纳高考体验
