高中数学 人教A版必修五课件 1.2 第1课时 距离和高度问题 :28张PPT
文档属性
| 名称 | 高中数学 人教A版必修五课件 1.2 第1课时 距离和高度问题 :28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览








文档简介
课件28张PPT。第1课时 距离和高度问题一、常用概念
1.基线
(1)定义:在测量上,根据测量需要适当确定的线段叫做基线.
(2)性质:在测量过程中,要根据实际需要选取合适的基线长度,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越高.
2.坡角与坡度3.视角
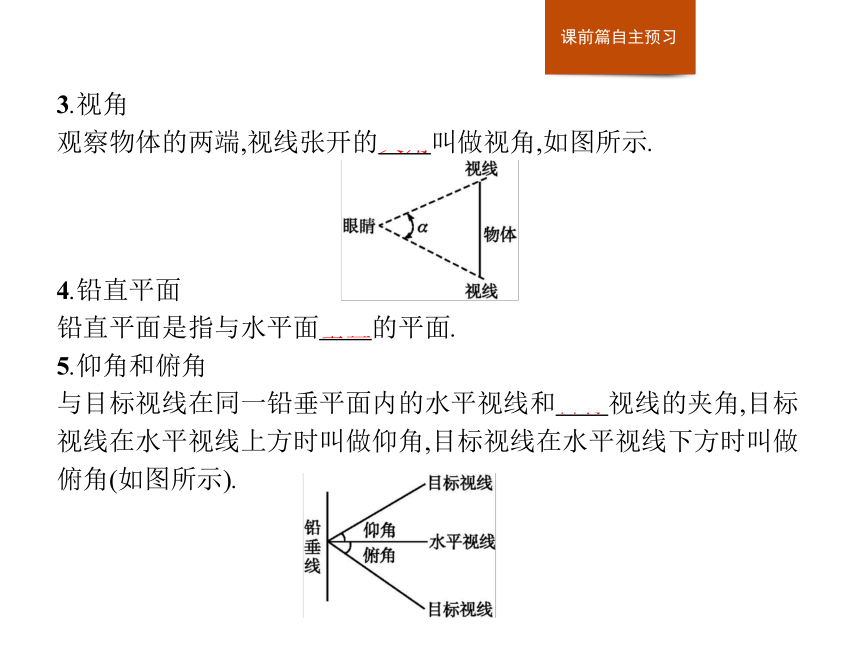
观察物体的两端,视线张开的夹角叫做视角,如图所示.4.铅直平面
铅直平面是指与水平面垂直的平面.
5.仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫做仰角,目标视线在水平视线下方时叫做俯角(如图所示).6.做一做:
(1)判断正误.
①坡面与水平面所成的二面角叫做坡角. ( )
②坡角越大,则坡比越小. ( )
答案:①√ ②×
(2)从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是( )
A.α>β B.α=β
C.α+β=90° D.α+β=180°
解析:如图,从A处望B处的仰角α与从B处望A处的俯角β是内错角,由水平线平行,得α=β.答案:B 二、解决实际测量问题的思路及步骤
1.基本思路2.一般步骤
(1)分析:理解题意,弄清已知与未知,画出示意图.
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型.
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解.
(4)检验:检验所求的解是否符合实际问题的意义,从而得出实际问题的解.3.做一做:
海上有A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B,C岛间的距离是( )答案:D 探究一探究二探究三思想方法当堂检测求可到达点与不可到达点之间的距离问题
例1如图 ,一名学生在河岸紧靠岸边笔直行走,开始在A处,
经观察,在河的对岸有一参照物C,与学生前进方向成30°角,学生前进200 m 后到达点B,测得该参照物与前进方向成75°角.
(1)求点A与参照物C的距离;
(2)求河的宽度.分析:根据图形,先由已知求出∠ACB,再利用正弦定理求得AC的长度,最后在直角三角形中求出河的宽度.探究一探究二探究三思想方法当堂检测探究一探究二探究三思想方法当堂检测反思感悟1.测量从一个可到达的点与一个不可到达的点之间的距离问题,一般可转化为已知两个角和一条边解三角形的问题,从而运用正弦定理去解决.
2.如图,点B为不可到达点,求A,B的距离的具体解题步骤是:
(1)取基线AC(尽量长),且使AB,AC不共线;探究一探究二探究三思想方法当堂检测变式训练1学校体育馆的人字屋架为等腰三角形,如图,测得AC的长度为4 m,∠A=30°,则其跨度AB的长为( )答案:D 探究一探究二探究三思想方法当堂检测求不可到达的两点之间的距离问题 例2如图,隔河看到两个目标A,B,但不能到达,在岸边选取相距 km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两个目标A,B之间的距离.
分析:要求出A,B之间的距离,把AB放在△ABC(或△ADB)中,但不管在哪个三角形中,AC,BC(或AD,BD)这些量都是未知的.把AC,BC(或AD,BD)放在△ACD,△BCD中求出它们的长即可.探究一探究二探究三思想方法当堂检测探究一探究二探究三思想方法当堂检测反思感悟1.测量两个不可到达的点之间的距离问题,一般是先把求距离问题转化为应用余弦定理求三角形的边长的问题,再把求未知的边长问题转化为只有一点不能到达的两点距离测量问题,最后运用正弦定理解决问题.2.如图所示,不可到达的A,B是地面上两点,要测量A,B两点之间的距离,具体步骤是:(1)取基线CD;(2)测量CD,∠ACB,∠BCD,∠ADC,∠BDA;(3)在△ACD中,解三角形得AC;在△BCD中,解三角形得BC;(4)在△ABC中,利用余弦定理得探究一探究二探究三思想方法当堂检测变式训练2如图,为了测量某湿地A,B两点间的距离,观察者找到在同一直线上的三点C,D,E.从D点测得∠ADC=67.5°,从C点测得∠ACD=45°,∠BCE=75°,从E点测得∠BEC=60°.若测得探究一探究二探究三思想方法当堂检测答案:C 探究一探究二探究三思想方法当堂检测求高度问题
例3如图,为了测量河对岸的塔高AB,选取与塔底B在同一水平面内的两个测点C和D,测得CD=200 m,在点C和点D测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.分析:先在Rt△ABC和Rt△ABD中,用AB表示BC和BD,再在△BCD中,由余弦定理建立方程求解.探究一探究二探究三思想方法当堂检测反思感悟1.在测量底部不可到达的建筑物的高度时,可以借助正弦定理或余弦定理,构造两角(两个仰角或两个俯角)和一边或三角(两个方向角和仰角)和一边,如图所示.探究一探究二探究三思想方法当堂检测2.解决测量高度问题的一般步骤是: 探究一探究二探究三思想方法当堂检测变式训练3如图,在山顶铁塔上B处测得一点A的俯角为α,在塔底C处测得A处的俯角为β.若铁塔高为m米,则山高CD为 米.?探究一探究二探究三思想方法当堂检测函数与方程思想在解三角形应用举例中的应用
典例 如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度(1)求索道AB的长;
(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?探究一探究二探究三思想方法当堂检测【审题视角】(1)利用正弦定理求出AB的长;(2)先设再建立时间t与甲、乙间距离d的函数关系式,利用关系式求最值.探究一探究二探究三思想方法当堂检测方法点睛与函数思想相联系的就是方程思想.所谓方程思想,就是在解决问题时,用事先设定的未知数沟通问题所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值,使问题获得解决,所设的未知数沟通了变量之间的联系.方程可以看做未知量与已知量相互制约的条件,它架设了由已知探索未知的桥梁.
函数与方程思想在数学中有着广泛的应用,在利用正、余弦定理求角或边长时,往往渗透着函数与方程思想.探究一探究二探究三思想方法当堂检测1.从地面上观察一建在山顶上的建筑物,测得其视角为α,同时测得建筑物顶部的仰角为β,则山顶的仰角为( )
A.α+β B.α-β
C.β-α D.α
解析:如图所示,AB表示建筑物,从地面上点C观察.由已知,得∠BCA=α,∠BCO=β,则山顶的仰角为∠OCA,∠OCA=∠BCO-∠BCA=β-α.答案:C 探究一探究二探究三思想方法当堂检测2.如图,从山顶A望地面上C,D两点,测得它们的俯角分别为45°和30°,已知CD=100 m,点C位于BD上,则山高AB等于( )答案:D 探究一探究二探究三思想方法当堂检测3.有一段长为10 m的斜坡,它的倾斜角为75°,在不改变坡高的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延伸 m.?探究一探究二探究三思想方法当堂检测的军事基地C和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,求蓝方这两支精锐部队之间的距离.探究一探究二探究三思想方法当堂检测
1.基线
(1)定义:在测量上,根据测量需要适当确定的线段叫做基线.
(2)性质:在测量过程中,要根据实际需要选取合适的基线长度,使测量具有较高的精确度.一般来说,基线越长,测量的精确度越高.
2.坡角与坡度3.视角
观察物体的两端,视线张开的夹角叫做视角,如图所示.4.铅直平面
铅直平面是指与水平面垂直的平面.
5.仰角和俯角
与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫做仰角,目标视线在水平视线下方时叫做俯角(如图所示).6.做一做:
(1)判断正误.
①坡面与水平面所成的二面角叫做坡角. ( )
②坡角越大,则坡比越小. ( )
答案:①√ ②×
(2)从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系是( )
A.α>β B.α=β
C.α+β=90° D.α+β=180°
解析:如图,从A处望B处的仰角α与从B处望A处的俯角β是内错角,由水平线平行,得α=β.答案:B 二、解决实际测量问题的思路及步骤
1.基本思路2.一般步骤
(1)分析:理解题意,弄清已知与未知,画出示意图.
(2)建模:根据已知条件与求解目标,把已知量与待求量尽可能地集中在有关三角形中,建立一个解三角形的数学模型.
(3)求解:利用正弦定理、余弦定理解三角形,求得数学模型的解.
(4)检验:检验所求的解是否符合实际问题的意义,从而得出实际问题的解.3.做一做:
海上有A,B两个小岛相距10海里,从A岛望C岛和B岛成60°的视角,从B岛望C岛和A岛成75°的视角,则B,C岛间的距离是( )答案:D 探究一探究二探究三思想方法当堂检测求可到达点与不可到达点之间的距离问题
例1如图 ,一名学生在河岸紧靠岸边笔直行走,开始在A处,
经观察,在河的对岸有一参照物C,与学生前进方向成30°角,学生前进200 m 后到达点B,测得该参照物与前进方向成75°角.
(1)求点A与参照物C的距离;
(2)求河的宽度.分析:根据图形,先由已知求出∠ACB,再利用正弦定理求得AC的长度,最后在直角三角形中求出河的宽度.探究一探究二探究三思想方法当堂检测探究一探究二探究三思想方法当堂检测反思感悟1.测量从一个可到达的点与一个不可到达的点之间的距离问题,一般可转化为已知两个角和一条边解三角形的问题,从而运用正弦定理去解决.
2.如图,点B为不可到达点,求A,B的距离的具体解题步骤是:
(1)取基线AC(尽量长),且使AB,AC不共线;探究一探究二探究三思想方法当堂检测变式训练1学校体育馆的人字屋架为等腰三角形,如图,测得AC的长度为4 m,∠A=30°,则其跨度AB的长为( )答案:D 探究一探究二探究三思想方法当堂检测求不可到达的两点之间的距离问题 例2如图,隔河看到两个目标A,B,但不能到达,在岸边选取相距 km的C,D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),求两个目标A,B之间的距离.
分析:要求出A,B之间的距离,把AB放在△ABC(或△ADB)中,但不管在哪个三角形中,AC,BC(或AD,BD)这些量都是未知的.把AC,BC(或AD,BD)放在△ACD,△BCD中求出它们的长即可.探究一探究二探究三思想方法当堂检测探究一探究二探究三思想方法当堂检测反思感悟1.测量两个不可到达的点之间的距离问题,一般是先把求距离问题转化为应用余弦定理求三角形的边长的问题,再把求未知的边长问题转化为只有一点不能到达的两点距离测量问题,最后运用正弦定理解决问题.2.如图所示,不可到达的A,B是地面上两点,要测量A,B两点之间的距离,具体步骤是:(1)取基线CD;(2)测量CD,∠ACB,∠BCD,∠ADC,∠BDA;(3)在△ACD中,解三角形得AC;在△BCD中,解三角形得BC;(4)在△ABC中,利用余弦定理得探究一探究二探究三思想方法当堂检测变式训练2如图,为了测量某湿地A,B两点间的距离,观察者找到在同一直线上的三点C,D,E.从D点测得∠ADC=67.5°,从C点测得∠ACD=45°,∠BCE=75°,从E点测得∠BEC=60°.若测得探究一探究二探究三思想方法当堂检测答案:C 探究一探究二探究三思想方法当堂检测求高度问题
例3如图,为了测量河对岸的塔高AB,选取与塔底B在同一水平面内的两个测点C和D,测得CD=200 m,在点C和点D测得塔顶A的仰角分别是45°和30°,且∠CBD=30°,求塔高AB.分析:先在Rt△ABC和Rt△ABD中,用AB表示BC和BD,再在△BCD中,由余弦定理建立方程求解.探究一探究二探究三思想方法当堂检测反思感悟1.在测量底部不可到达的建筑物的高度时,可以借助正弦定理或余弦定理,构造两角(两个仰角或两个俯角)和一边或三角(两个方向角和仰角)和一边,如图所示.探究一探究二探究三思想方法当堂检测2.解决测量高度问题的一般步骤是: 探究一探究二探究三思想方法当堂检测变式训练3如图,在山顶铁塔上B处测得一点A的俯角为α,在塔底C处测得A处的俯角为β.若铁塔高为m米,则山高CD为 米.?探究一探究二探究三思想方法当堂检测函数与方程思想在解三角形应用举例中的应用
典例 如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度(1)求索道AB的长;
(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?探究一探究二探究三思想方法当堂检测【审题视角】(1)利用正弦定理求出AB的长;(2)先设再建立时间t与甲、乙间距离d的函数关系式,利用关系式求最值.探究一探究二探究三思想方法当堂检测方法点睛与函数思想相联系的就是方程思想.所谓方程思想,就是在解决问题时,用事先设定的未知数沟通问题所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值,使问题获得解决,所设的未知数沟通了变量之间的联系.方程可以看做未知量与已知量相互制约的条件,它架设了由已知探索未知的桥梁.
函数与方程思想在数学中有着广泛的应用,在利用正、余弦定理求角或边长时,往往渗透着函数与方程思想.探究一探究二探究三思想方法当堂检测1.从地面上观察一建在山顶上的建筑物,测得其视角为α,同时测得建筑物顶部的仰角为β,则山顶的仰角为( )
A.α+β B.α-β
C.β-α D.α
解析:如图所示,AB表示建筑物,从地面上点C观察.由已知,得∠BCA=α,∠BCO=β,则山顶的仰角为∠OCA,∠OCA=∠BCO-∠BCA=β-α.答案:C 探究一探究二探究三思想方法当堂检测2.如图,从山顶A望地面上C,D两点,测得它们的俯角分别为45°和30°,已知CD=100 m,点C位于BD上,则山高AB等于( )答案:D 探究一探究二探究三思想方法当堂检测3.有一段长为10 m的斜坡,它的倾斜角为75°,在不改变坡高的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延伸 m.?探究一探究二探究三思想方法当堂检测的军事基地C和D处测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°,如图所示,求蓝方这两支精锐部队之间的距离.探究一探究二探究三思想方法当堂检测
