高中数学 人教A版必修五课件 3.4 第1课时 基本不等式 :29张PPT
文档属性
| 名称 | 高中数学 人教A版必修五课件 3.4 第1课时 基本不等式 :29张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览








文档简介
课件29张PPT。第1课时 基本不等式一、重要不等式
填空:重要不等式
一般地,对于任意实数a,b,有a2+b2≥2ab,当且仅当a=b时,等号成立.
二、基本不等式
1.填空:
(1)基本不等式答案:①√ ②× ③√ 解析:由重要不等式可知选项A,B成立,由基本不等式可知选项D成立,选项C不成立.故选C.
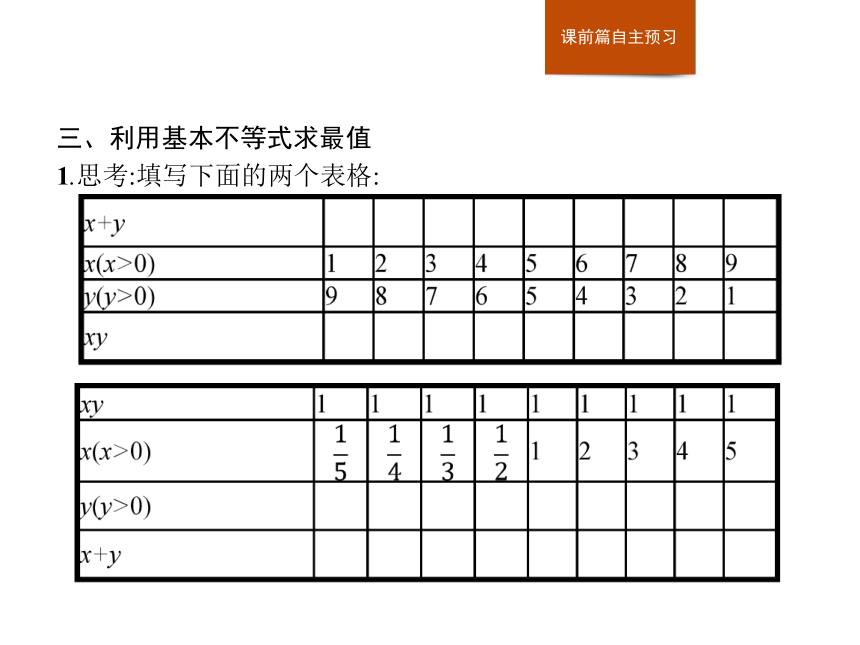
答案:C三、利用基本不等式求最值
1.思考:填写下面的两个表格:根据以上表格,并结合基本不等式分析:
(1)当x+y是定值时,xy有最大值还是最小值?最值等于什么?
(2)当xy是定值时,x+y有最大值还是最小值?最值等于什么?2.填空:
基本不等式与最值
已知x,y都是正数.
(1)若x+y=s(和为定值),则当x=y时,积xy取得最大值.
(2)若xy=p(积为定值),则当x=y时,和x+y取得最小值.答案:①× ②× ③×(2)已知x>0,y>0.
①若xy=4,则x+y的最小值是 ;?
②若x+y=4,则xy的最大值是 .?答案:①4 ②4 探究一探究二探究三思维辨析当堂检测对基本不等式的理解 分析:从基本不等式成立的条件以及基本不等式的变形入手,对每一个结论分别进行研究,找出其中的正确结论.探究一探究二探究三思维辨析当堂检测答案:④
反思感悟要熟记重要不等式和基本不等式的形式及其成立的条件,尽管在这两个不等式中,a,b可以换成不同的数、式,但换后的数、式必须满足相应的条件,否则就会得出错误的结论.探究一探究二探究三思维辨析当堂检测答案:C 探究一探究二探究三思维辨析当堂检测利用基本不等式证明不等式 探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测反思感悟1.利用基本不等式证明不等式,关键是所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,从而达到放缩的目的.
2.注意多次运用基本不等式时等号能否取到.
3.解题时要注意技巧,当不能直接利用基本不等式时,可将原不等式进行组合、构造,以满足能使用基本不等式的形式.
4.在证明不等式的过程中,注意充分利用“1的代换”,即把常数“1”替换为已知的式子,然后经过整理后再利用基本不等式进行证明.探究一探究二探究三思维辨析当堂检测变式训练2(1)已知a,b,c,d都是正数,求证:(ab+cd)(ac+bd)≥4abcd.探究一探究二探究三思维辨析当堂检测利用基本不等式求最值 (2)若lg a+lg b=2,求a+b的最小值;
(3)若实数x,y满足x+y=-1,求2x+2y的最小值.
分析:利用基本不等式求最值,先从已知条件或函数中找到定和或定积,再利用基本不等式求解.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测延伸探究本例(2)中,若将条件改为“a>1,b>1,且ab=1 000”,再求lg a·lg b的最大值.探究一探究二探究三思维辨析当堂检测忽视基本不等式成立的条件致误 提示:由于函数的定义域为(-∞,0)∪(0,+∞),错解中运用基本不等式时,忽视了基本不等式成立的条件,没有对x∈(-∞,0)的情况进行求解,从而导致错误.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测答案:C 探究一探究二探究三思维辨析当堂检测答案:A 3.已知00)是a,b的等比中项,则A与G的大小关系是 .?答案:A≥G 探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测
填空:重要不等式
一般地,对于任意实数a,b,有a2+b2≥2ab,当且仅当a=b时,等号成立.
二、基本不等式
1.填空:
(1)基本不等式答案:①√ ②× ③√ 解析:由重要不等式可知选项A,B成立,由基本不等式可知选项D成立,选项C不成立.故选C.
答案:C三、利用基本不等式求最值
1.思考:填写下面的两个表格:根据以上表格,并结合基本不等式分析:
(1)当x+y是定值时,xy有最大值还是最小值?最值等于什么?
(2)当xy是定值时,x+y有最大值还是最小值?最值等于什么?2.填空:
基本不等式与最值
已知x,y都是正数.
(1)若x+y=s(和为定值),则当x=y时,积xy取得最大值.
(2)若xy=p(积为定值),则当x=y时,和x+y取得最小值.答案:①× ②× ③×(2)已知x>0,y>0.
①若xy=4,则x+y的最小值是 ;?
②若x+y=4,则xy的最大值是 .?答案:①4 ②4 探究一探究二探究三思维辨析当堂检测对基本不等式的理解 分析:从基本不等式成立的条件以及基本不等式的变形入手,对每一个结论分别进行研究,找出其中的正确结论.探究一探究二探究三思维辨析当堂检测答案:④
反思感悟要熟记重要不等式和基本不等式的形式及其成立的条件,尽管在这两个不等式中,a,b可以换成不同的数、式,但换后的数、式必须满足相应的条件,否则就会得出错误的结论.探究一探究二探究三思维辨析当堂检测答案:C 探究一探究二探究三思维辨析当堂检测利用基本不等式证明不等式 探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测反思感悟1.利用基本不等式证明不等式,关键是所证不等式中必须有“和”式或“积”式,通过将“和”式转化为“积”式或将“积”式转化为“和”式,从而达到放缩的目的.
2.注意多次运用基本不等式时等号能否取到.
3.解题时要注意技巧,当不能直接利用基本不等式时,可将原不等式进行组合、构造,以满足能使用基本不等式的形式.
4.在证明不等式的过程中,注意充分利用“1的代换”,即把常数“1”替换为已知的式子,然后经过整理后再利用基本不等式进行证明.探究一探究二探究三思维辨析当堂检测变式训练2(1)已知a,b,c,d都是正数,求证:(ab+cd)(ac+bd)≥4abcd.探究一探究二探究三思维辨析当堂检测利用基本不等式求最值 (2)若lg a+lg b=2,求a+b的最小值;
(3)若实数x,y满足x+y=-1,求2x+2y的最小值.
分析:利用基本不等式求最值,先从已知条件或函数中找到定和或定积,再利用基本不等式求解.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测延伸探究本例(2)中,若将条件改为“a>1,b>1,且ab=1 000”,再求lg a·lg b的最大值.探究一探究二探究三思维辨析当堂检测忽视基本不等式成立的条件致误 提示:由于函数的定义域为(-∞,0)∪(0,+∞),错解中运用基本不等式时,忽视了基本不等式成立的条件,没有对x∈(-∞,0)的情况进行求解,从而导致错误.探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测答案:C 探究一探究二探究三思维辨析当堂检测答案:A 3.已知0
