高中数学 人教A版必修五课件 1.2 第2课时 角度问题 :26张PPT
文档属性
| 名称 | 高中数学 人教A版必修五课件 1.2 第2课时 角度问题 :26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 13:16:06 | ||
图片预览






文档简介
课件26张PPT。第2课时 角度问题一、有关概念
1.方位角与方向角
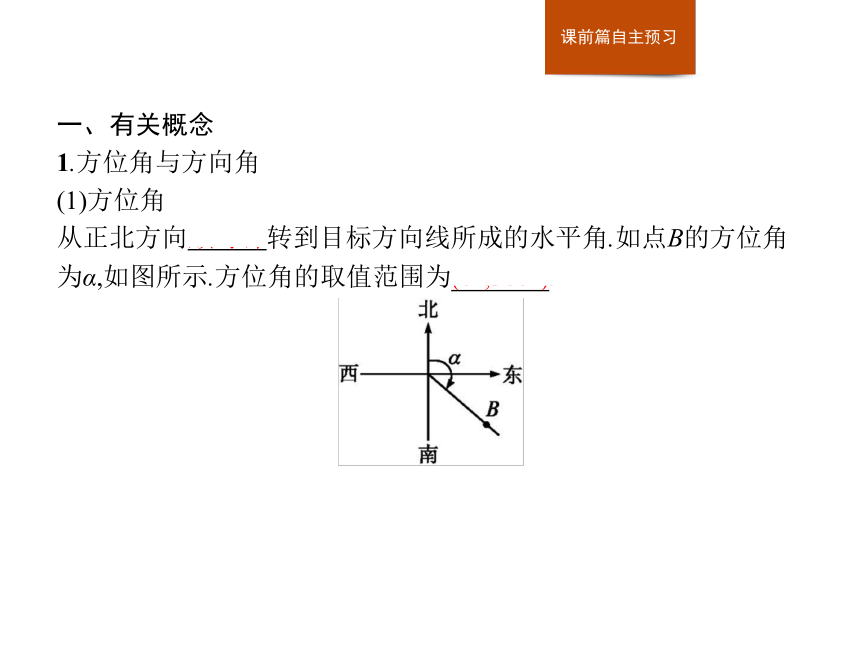
(1)方位角
从正北方向顺时针转到目标方向线所成的水平角.如点B的方位角为α,如图所示.方位角的取值范围为(0°,360°).(2)方向角
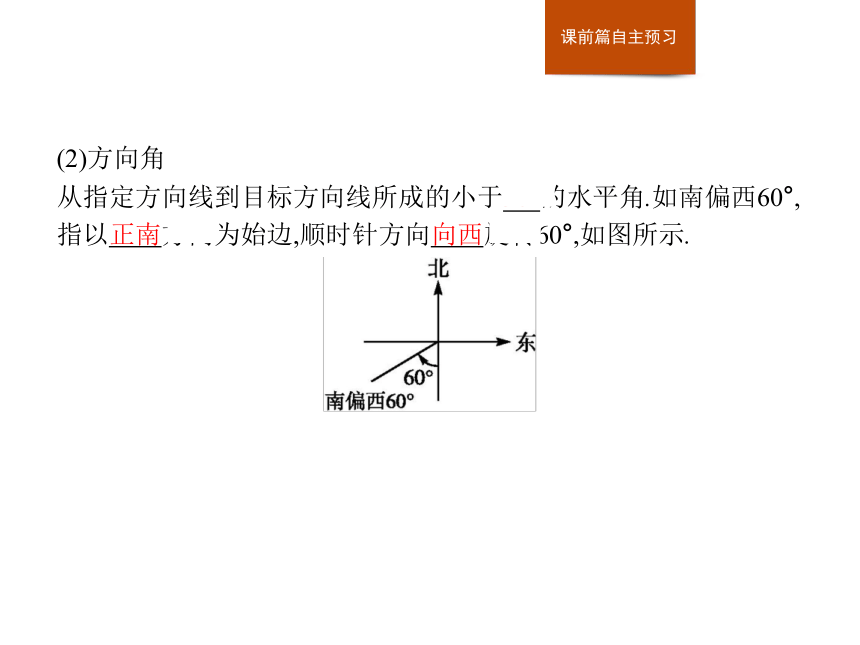
从指定方向线到目标方向线所成的小于90°的水平角.如南偏西60°,指以正南方向为始边,顺时针方向向西旋转60°,如图所示.2.做一做:
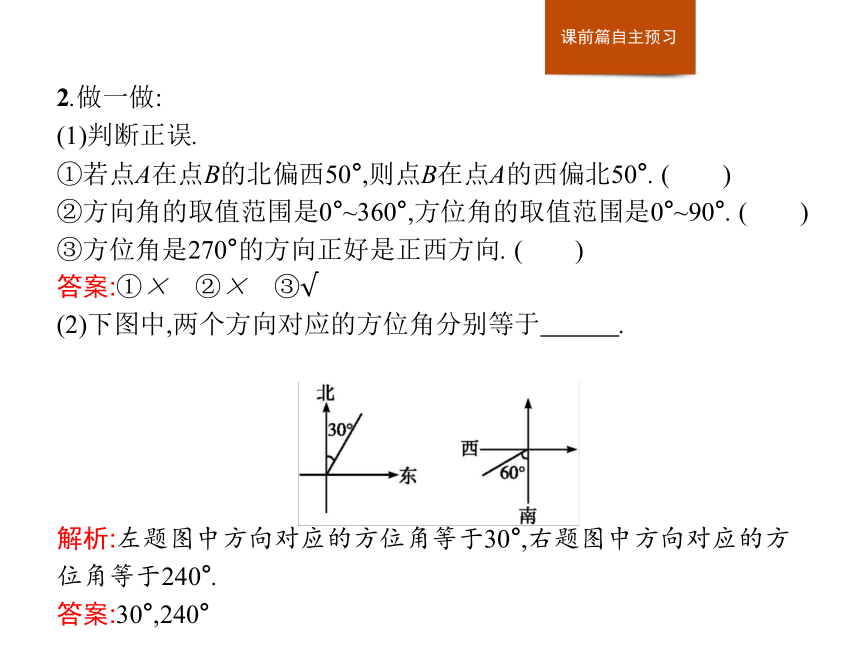
(1)判断正误.
①若点A在点B的北偏西50°,则点B在点A的西偏北50°. ( )
②方向角的取值范围是0°~360°,方位角的取值范围是0°~90°. ( )
③方位角是270°的方向正好是正西方向. ( )
答案:①× ②× ③√
(2)下图中,两个方向对应的方位角分别等于 .?解析:左题图中方向对应的方位角等于30°,右题图中方向对应的方位角等于240°.
答案:30°,240°二、用正、余弦定理解决与角度有关问题
思考:怎样用正、余弦定理解决与角度有关的问题?
提示:测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,先从实际问题中抽象出一个或几个三角形,再通过解这些三角形,得到所求的量,从而得到实际问题的解.解题时应认真审题,结合图形去选择定理,这是最关键、最重要的一步.探究一探究二探究三当堂检测实际测量中的角度问题
例1地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离他40 m,之后该测绘人员沿正北方向行走了40 m,达到点B.试确定此时目标参照物P相对于他的方位角以及他与目标参照物P的距离.
分析:画出图形,在三角形中,利用正弦定理求出内角的大小以及边的长度,从而确定相应的方位角以及距离.探究一探究二探究三当堂检测因为AB=40 m,所以AB=PB,所以∠APB=∠PAB=30°,所以∠PBA=120°.因此测绘人员到达点B时,目标参照物P相对于该测绘人员的方位角为180°-120°=60°,且目标参照物P与他的距离为40 m.探究一探究二探究三当堂检测反思感悟解决实际测量中的角度问题的基本步骤:
(1)找准观测点以及参照物,根据“上北下南,左西右东”确定正北方向;
(2)根据题意作出示意图;
(3)分析图中的已知量和未知量,标出有关角和线段的大小;
(4)利用正弦定理或余弦定理解三角形,求出未知量.探究一探究二探究三当堂检测变式训练1如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.探究一探究二探究三当堂检测?∴∠CAD≈24.3°.
∴从A到D的方位角约为50°+19.5°+24.3°=93.8°.
即从A到D的方位角约为93.8°,距离约为1 531 m.探究一探究二探究三当堂检测航海与追及中的角度问题
例2某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,立即测出该渔轮在方位角为45°,距离为10 n mile的C处,并测得渔轮正沿方位角为105°的方向,以9 n mile/h的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.
分析:本题中所涉及的路程在不断变化,但舰艇和渔轮相遇时所用时间相等,先设出所用时间t,找出等量关系,再解三角形.探究一探究二探究三当堂检测解:如图所示,根据题意可知AC=10 n mile,∠ACB=120°.设舰艇靠近渔轮所需的时间为t h,并在B处与渔轮相遇,
则AB=21t n mile,BC=9t n mile.在△ABC中,由余弦定理,得探究一探究二探究三当堂检测即∠CAB≈21.8°.
故舰艇航行的方位角为45°+21.8°=66.8°.反思感悟1.本题欲求方位角,先求边长,而要求边长,需先求时间.由于舰艇与渔轮同时在移动,因此相遇点不确定,即舰艇的航向不确定,解题时画图的关键是设出相遇点B,画出可以求解的三角形.
2.解决这类问题,首先明确题中所给各个角的含义,然后分析题意,根据题意画出正确的示意图,将实际问题转化为数学问题,运用正弦定理或余弦定理求解,体现了数形结合与方程的数学思想方法.探究一探究二探究三当堂检测延伸探究本题中其他条件不变,将“渔轮向小岛靠拢的速度”改为“10 n mile/h”,将“我海军舰艇的速度”改为“10 n mile/h”,求舰艇的航向和靠近渔轮所需要的时间.探究一探究二探究三当堂检测物理中的角度问题
例3在点O观测到远处有一物体在做匀速直线运动,开始时刻物体位于点P,一分钟后,该物体位于点Q,且∠POQ=90°,再过一分钟,该物体位于点R,且∠QOR=30°,则tan∠OPQ= .?
分析:结合题意画出图形,在图形中利用正、余弦定理求解.
解析:由物体做匀速直线运动,得PQ=QR,不妨设其长度为1.如图,探究一探究二探究三当堂检测探究一探究二探究三当堂检测变式训练2作用在同一点的三个力F1,F2,F3平衡,已知|F1|=30 N,|F2|=50 N,F1与F2的夹角是60°,则F3与F1的夹角的正弦值为 .?
解析:由题意,得F3应和F1,F2的合力F平衡.设F3与F1的夹角为θ,如图,当三力平衡时,由余弦定理,得探究一探究二探究三当堂检测1.如图,点A在北偏西65°的方向上,则其方位角等于( )
A.25° B.65° C.245° D.295°解析:方位角等于360°-65°=295°.
答案:D探究一探究二探究三当堂检测2.如图,在某海岸A处,发现北偏东30°方向,距离A处1海里的B处有一艘走私船,在A处北偏西60°的方向,距离A处 海里的C处的缉私船奉命以5 海里/小时的速度追截走私船.此时,走私船正以5海里/小时的速度从B处按照北偏东30°方向逃窜,则缉私船沿( )方向能最快追上走私船.
A.北偏东30° B.北偏东45°
C.北偏东60° D.正东探究一探究二探究三当堂检测答案:C 探究一探究二探究三当堂检测3.一艘轮船从A出发,沿南偏东70°的方向航行40 n mile后到达海岛B,然后从B出发,沿北偏东35°的方向航行了40 n mile到达海岛C.如果下次航行直接从A出发到C,那么此船航行的方向和路程分别为( )探究一探究二探究三当堂检测答案:C 探究一探究二探究三当堂检测4.在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水中漂行,此时风向是北偏东30°,风速是20 km/h,水的流向是正东,流速是20 km/h.若不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东 ?,大小为 ? km/h.?
解析:如图,∠AOB=60°.由余弦定理,得OC2=202+202-2×20×20cos 120°=1 200,探究一探究二探究三当堂检测5.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12 n mile,渔船乙以10 n mile/h 的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上.
(1)求渔船甲的速度;
(2)求sin α的值.探究一探究二探究三当堂检测解:(1)在△ABC中,∠BAC=180°-60°=120°,AB=12 n mile,AC=10×2=20(n mile),∠BCA=α.
由余弦定理,
得BC2=AB2+AC2-2AB·AC·cos∠BAC
=122+202-2×12×20×cos 120°=784,
解得BC=28 n mile.
1.方位角与方向角
(1)方位角
从正北方向顺时针转到目标方向线所成的水平角.如点B的方位角为α,如图所示.方位角的取值范围为(0°,360°).(2)方向角
从指定方向线到目标方向线所成的小于90°的水平角.如南偏西60°,指以正南方向为始边,顺时针方向向西旋转60°,如图所示.2.做一做:
(1)判断正误.
①若点A在点B的北偏西50°,则点B在点A的西偏北50°. ( )
②方向角的取值范围是0°~360°,方位角的取值范围是0°~90°. ( )
③方位角是270°的方向正好是正西方向. ( )
答案:①× ②× ③√
(2)下图中,两个方向对应的方位角分别等于 .?解析:左题图中方向对应的方位角等于30°,右题图中方向对应的方位角等于240°.
答案:30°,240°二、用正、余弦定理解决与角度有关问题
思考:怎样用正、余弦定理解决与角度有关的问题?
提示:测量角度问题主要是指在海上或空中测量角度的问题,如确定目标的方位,观察某一建筑物的视角等.解决它们的关键是根据题意和图形及有关概念,确定所求的角在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,先从实际问题中抽象出一个或几个三角形,再通过解这些三角形,得到所求的量,从而得到实际问题的解.解题时应认真审题,结合图形去选择定理,这是最关键、最重要的一步.探究一探究二探究三当堂检测实际测量中的角度问题
例1地图测绘人员在点A测得某一目标参照物P在他的北偏东30°的方向,且距离他40 m,之后该测绘人员沿正北方向行走了40 m,达到点B.试确定此时目标参照物P相对于他的方位角以及他与目标参照物P的距离.
分析:画出图形,在三角形中,利用正弦定理求出内角的大小以及边的长度,从而确定相应的方位角以及距离.探究一探究二探究三当堂检测因为AB=40 m,所以AB=PB,所以∠APB=∠PAB=30°,所以∠PBA=120°.因此测绘人员到达点B时,目标参照物P相对于该测绘人员的方位角为180°-120°=60°,且目标参照物P与他的距离为40 m.探究一探究二探究三当堂检测反思感悟解决实际测量中的角度问题的基本步骤:
(1)找准观测点以及参照物,根据“上北下南,左西右东”确定正北方向;
(2)根据题意作出示意图;
(3)分析图中的已知量和未知量,标出有关角和线段的大小;
(4)利用正弦定理或余弦定理解三角形,求出未知量.探究一探究二探究三当堂检测变式训练1如图所示,从A到B,方位角是50°,距离是470 m;从B到C,方位角是80°,距离是860 m;从C到D,方位角是150°,距离是640 m,试计算从A到D的方位角和距离.探究一探究二探究三当堂检测?∴∠CAD≈24.3°.
∴从A到D的方位角约为50°+19.5°+24.3°=93.8°.
即从A到D的方位角约为93.8°,距离约为1 531 m.探究一探究二探究三当堂检测航海与追及中的角度问题
例2某渔轮在航行中不幸遇险,发出呼救信号,我海军舰艇在A处获悉后,立即测出该渔轮在方位角为45°,距离为10 n mile的C处,并测得渔轮正沿方位角为105°的方向,以9 n mile/h的速度向某小岛靠拢,我海军舰艇立即以21 n mile/h的速度前去营救,求舰艇的航向和靠近渔轮所需的时间.
分析:本题中所涉及的路程在不断变化,但舰艇和渔轮相遇时所用时间相等,先设出所用时间t,找出等量关系,再解三角形.探究一探究二探究三当堂检测解:如图所示,根据题意可知AC=10 n mile,∠ACB=120°.设舰艇靠近渔轮所需的时间为t h,并在B处与渔轮相遇,
则AB=21t n mile,BC=9t n mile.在△ABC中,由余弦定理,得探究一探究二探究三当堂检测即∠CAB≈21.8°.
故舰艇航行的方位角为45°+21.8°=66.8°.反思感悟1.本题欲求方位角,先求边长,而要求边长,需先求时间.由于舰艇与渔轮同时在移动,因此相遇点不确定,即舰艇的航向不确定,解题时画图的关键是设出相遇点B,画出可以求解的三角形.
2.解决这类问题,首先明确题中所给各个角的含义,然后分析题意,根据题意画出正确的示意图,将实际问题转化为数学问题,运用正弦定理或余弦定理求解,体现了数形结合与方程的数学思想方法.探究一探究二探究三当堂检测延伸探究本题中其他条件不变,将“渔轮向小岛靠拢的速度”改为“10 n mile/h”,将“我海军舰艇的速度”改为“10 n mile/h”,求舰艇的航向和靠近渔轮所需要的时间.探究一探究二探究三当堂检测物理中的角度问题
例3在点O观测到远处有一物体在做匀速直线运动,开始时刻物体位于点P,一分钟后,该物体位于点Q,且∠POQ=90°,再过一分钟,该物体位于点R,且∠QOR=30°,则tan∠OPQ= .?
分析:结合题意画出图形,在图形中利用正、余弦定理求解.
解析:由物体做匀速直线运动,得PQ=QR,不妨设其长度为1.如图,探究一探究二探究三当堂检测探究一探究二探究三当堂检测变式训练2作用在同一点的三个力F1,F2,F3平衡,已知|F1|=30 N,|F2|=50 N,F1与F2的夹角是60°,则F3与F1的夹角的正弦值为 .?
解析:由题意,得F3应和F1,F2的合力F平衡.设F3与F1的夹角为θ,如图,当三力平衡时,由余弦定理,得探究一探究二探究三当堂检测1.如图,点A在北偏西65°的方向上,则其方位角等于( )
A.25° B.65° C.245° D.295°解析:方位角等于360°-65°=295°.
答案:D探究一探究二探究三当堂检测2.如图,在某海岸A处,发现北偏东30°方向,距离A处1海里的B处有一艘走私船,在A处北偏西60°的方向,距离A处 海里的C处的缉私船奉命以5 海里/小时的速度追截走私船.此时,走私船正以5海里/小时的速度从B处按照北偏东30°方向逃窜,则缉私船沿( )方向能最快追上走私船.
A.北偏东30° B.北偏东45°
C.北偏东60° D.正东探究一探究二探究三当堂检测答案:C 探究一探究二探究三当堂检测3.一艘轮船从A出发,沿南偏东70°的方向航行40 n mile后到达海岛B,然后从B出发,沿北偏东35°的方向航行了40 n mile到达海岛C.如果下次航行直接从A出发到C,那么此船航行的方向和路程分别为( )探究一探究二探究三当堂检测答案:C 探究一探究二探究三当堂检测4.在一次抗洪抢险中,某救生艇发动机突然发生故障停止转动,失去动力的救生艇在洪水中漂行,此时风向是北偏东30°,风速是20 km/h,水的流向是正东,流速是20 km/h.若不考虑其他因素,救生艇在洪水中漂行的速度的方向为北偏东 ?,大小为 ? km/h.?
解析:如图,∠AOB=60°.由余弦定理,得OC2=202+202-2×20×20cos 120°=1 200,探究一探究二探究三当堂检测5.如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12 n mile,渔船乙以10 n mile/h 的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上.
(1)求渔船甲的速度;
(2)求sin α的值.探究一探究二探究三当堂检测解:(1)在△ABC中,∠BAC=180°-60°=120°,AB=12 n mile,AC=10×2=20(n mile),∠BCA=α.
由余弦定理,
得BC2=AB2+AC2-2AB·AC·cos∠BAC
=122+202-2×12×20×cos 120°=784,
解得BC=28 n mile.
