高中数学 人教A版必修五课件 2.4 第2课时 等比数列的性质及应用 :23张PPT
文档属性
| 名称 | 高中数学 人教A版必修五课件 2.4 第2课时 等比数列的性质及应用 :23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 609.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览






文档简介
课件23张PPT。第2课时 等比数列的性质及应用等比数列的常用性质
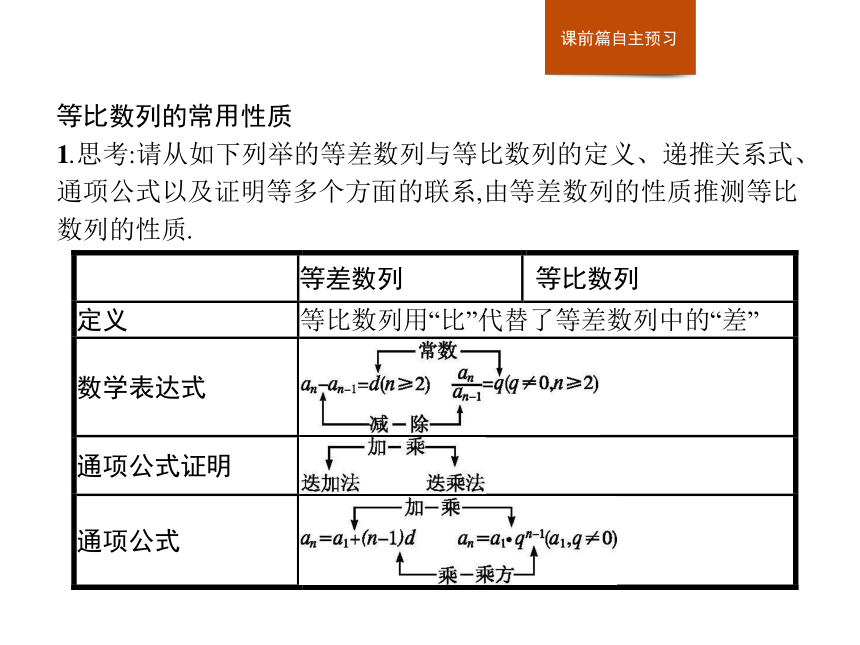
1.思考:请从如下列举的等差数列与等比数列的定义、递推关系式、通项公式以及证明等多个方面的联系,由等差数列的性质推测等比数列的性质.2.填空:
等比数列的常用性质
(1)若m+n=p+q(m,n,p,q∈N*),则am·an=ap·aq.
特例:若m+n=2p(m,n,p∈N*),则am·an= .
(2)an=am·qn-m(m,n∈N*).
(3)在等比数列{an}中,每隔k项取出一项,取出的项按原来顺序组成新数列,该数列仍然是等比数列,公比为qk+1.3.做一做:
(1)判断正误.
①在等比数列{an}中,若aman=apaq,则m+n=p+q. ( )
②等比数列去掉前面若干项后,余下的项仍构成等比数列. ( )
③若数列{an}是等比数列,则{an+an+1}也是等比数列. ( )
④在等比数列{an}中,若m+n=p,则aman=ap. ( )
答案:①× ②√ ③× ④×
(2)在等比数列{an}中,若a1a9=9,则a4a6=( )
A.3 B.±3 C.9 D.±9
答案:C4.思考:当等比数列的公比q>1时,该等比数列是递增数列吗?等比数列的单调性与等比数列的哪些量有关?
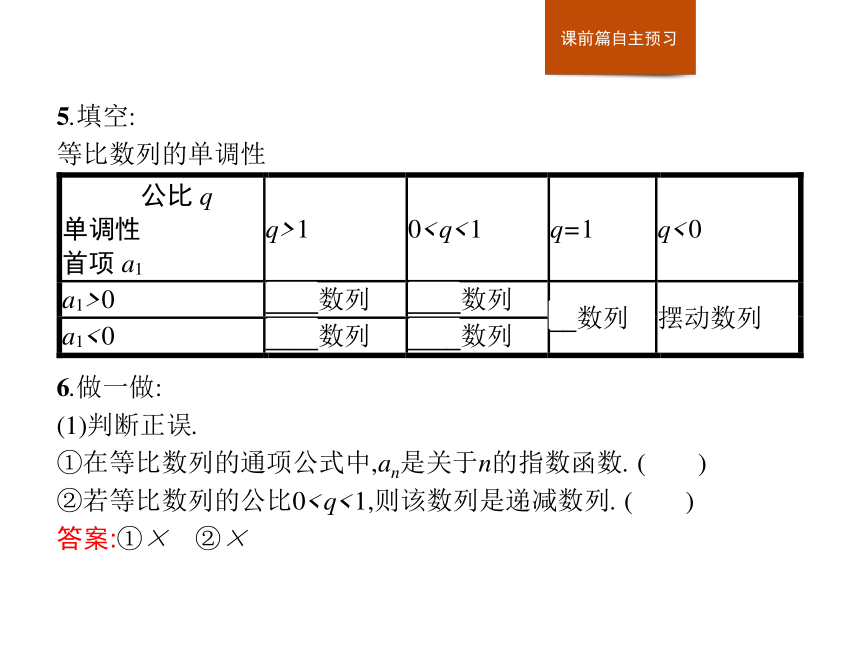
提示:不一定;等比数列的单调性与等比数列的首项a1,q的正负有关.5.填空:
等比数列的单调性6.做一做:
(1)判断正误.
①在等比数列的通项公式中,an是关于n的指数函数. ( )
②若等比数列的公比0答案:①× ②×(2)①在等比数列{an}中,首项a1<0,要使数列{an}对任意正整数n都有an+1>an,则公比q应满足( )
A.q>1 B.0解析:①an+1-an=a1qn-1(q-1)>0,
因为a1<0,所以0②∵a2=2,a4=8,又数列{an}是递增数列,∴q=2.
答案:①B ②2探究一探究二探究三当堂检测等比数列性质的应用 探究一探究二探究三当堂检测反思感悟1.等比数列的性质是等比数列的定义、通项公式等基础知识的推广与变形,熟练掌握和灵活应用这些性质可以有效、方便、快捷地解决许多等比数列问题.
2.应用等比数列的性质解题的关键是发现问题中涉及的数列各项的下标之间的关系,充分利用①若m+n=p+q(m,n,p,q∈N*),则探究一探究二探究三当堂检测变式训练1(1)在等比数列{an}中,a1,a99是方程x2-10x+16=0的两个根,则a50的值为( )
A.10 B.16 C.±4 D.4
(2)在等比数列{an}中,a1a2=1,a5a6=9,则a3a4=( )解析:(1)依题意,得a1·a99=16,而a1·a99= ,所以a50=±4.
(2)在等比数列{an}中,a1a2=1,a5a6=9,
所以a1a2a5a6=9.又a3a4=a1a6=a2a5,所以(a3a4)2=9.又a3a4与a1a2的符号相同,故a3a4=3.
答案:(1)C (2)A探究一探究二探究三当堂检测等比数列的综合问题
例2有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数和第四个数的和是16,中间两个数的和是12.求这四个数.
分析:根据条件,用两个未知数表示这四个数.所以,当a=4,d=4时,所求四个数为0,4,8,16;
当a=9,d=-6时,所求四个数为15,9,3,1.
故所求四个数为0,4,8,16或15,9,3,1.探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究一探究二探究三当堂检测延伸探究将本例中的条件改为“有四个实数,前三个数依次成等比数列,它们的积是-8,后三个数依次成等差数列,它们的积为-80”,再求这四个数.探究一探究二探究三当堂检测等比数列的实际应用
例3为了治理“沙尘暴”,西部某地区政府经过多年努力,到2016年底,将当地沙漠绿化了40%,从2017年开始,每年将出现这种现象:原有沙漠面积的12%被绿化,即改造为绿洲(被绿化的部分叫绿洲),同时原有绿洲面积的8%又被侵蚀为沙漠,问至少经过几年的绿化,才能使该地区的绿洲面积超过50%?(可参考数据lg 2≈0.3,最后结果精确到整数)
分析:依题意,每年的沙漠面积与绿洲面积之和是确定的,另外需根据题意建立前后两年绿洲面积之间的关系,由此构造等比数列解决问题.探究一探究二探究三当堂检测探究一探究二探究三当堂检测所以至少经过4年才能使该地区的绿洲面积超过50%.探究一探究二探究三当堂检测反思感悟1.一般地,涉及产值增长率问题、银行利息问题、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解.
2.建立等比数列模型进行运算时,往往涉及指数、对数方程或不等式的问题,要注意运算的正确性,还要善于进行估算,对于近似计算问题,答案要符合实际问题的需要.探究一探究二探究三当堂检测变式训练2一种专门占据内存的计算机病毒开始时占据内存2 KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后 分钟,该病毒占据内存64 MB(1 MB=210 KB).?
解析:由题意,得每3分钟病毒占的内存容量构成一个等比数列,设病毒占据64 MB时自身复制了n次,即2×2n=64×210=216,解得n=15,从而复制的时间为15×3=45(分钟).
答案:45探究一探究二探究三当堂检测1.对任意等比数列{an},下列说法一定正确的是( )
A.a1,a3,a9成等比数列 B.a2,a3,a6成等比数列
C.a2,a4,a8成等比数列 D.a3,a6,a9成等比数列
解析:根据等比数列的性质,若m+n=2k(m,n,k∈N*),则am,ak,an成等比数列.
即a3,a6,a9成等比数列.故选D.
答案:D
2.在等比数列{an}中,若a2=8,a5=64,则公比q为( )
A.2 B.3 C.4 D.8
解析:由a5=a2q3,得q3=8,所以q=2.
答案:A探究一探究二探究三当堂检测3.一张报纸的厚度为a,面积为b,现将此报纸对折(沿对边中点连线折叠)7次,这时报纸的厚度和面积分别为 ( )答案:C 探究一探究二探究三当堂检测4.在等比数列{an}中,a1+a2=30,a3+a4=120,则a5+a6= .?
解析:根据等比数列的性质可知a1+a2,a3+a4,a5+a6也成等比数列,即(a3+a4)2=(a1+a2)(a5+a6),答案:480 探究一探究二探究三当堂检测5.已知数列{an}为等比数列.
(1)若a1+a2+a3=21,a1a2a3=216,求an;
(2)若a3a5=18,a4a8=72,求公比q.
1.思考:请从如下列举的等差数列与等比数列的定义、递推关系式、通项公式以及证明等多个方面的联系,由等差数列的性质推测等比数列的性质.2.填空:
等比数列的常用性质
(1)若m+n=p+q(m,n,p,q∈N*),则am·an=ap·aq.
特例:若m+n=2p(m,n,p∈N*),则am·an= .
(2)an=am·qn-m(m,n∈N*).
(3)在等比数列{an}中,每隔k项取出一项,取出的项按原来顺序组成新数列,该数列仍然是等比数列,公比为qk+1.3.做一做:
(1)判断正误.
①在等比数列{an}中,若aman=apaq,则m+n=p+q. ( )
②等比数列去掉前面若干项后,余下的项仍构成等比数列. ( )
③若数列{an}是等比数列,则{an+an+1}也是等比数列. ( )
④在等比数列{an}中,若m+n=p,则aman=ap. ( )
答案:①× ②√ ③× ④×
(2)在等比数列{an}中,若a1a9=9,则a4a6=( )
A.3 B.±3 C.9 D.±9
答案:C4.思考:当等比数列的公比q>1时,该等比数列是递增数列吗?等比数列的单调性与等比数列的哪些量有关?
提示:不一定;等比数列的单调性与等比数列的首项a1,q的正负有关.5.填空:
等比数列的单调性6.做一做:
(1)判断正误.
①在等比数列的通项公式中,an是关于n的指数函数. ( )
②若等比数列的公比0
A.q>1 B.0
因为a1<0,所以0
答案:①B ②2探究一探究二探究三当堂检测等比数列性质的应用 探究一探究二探究三当堂检测反思感悟1.等比数列的性质是等比数列的定义、通项公式等基础知识的推广与变形,熟练掌握和灵活应用这些性质可以有效、方便、快捷地解决许多等比数列问题.
2.应用等比数列的性质解题的关键是发现问题中涉及的数列各项的下标之间的关系,充分利用①若m+n=p+q(m,n,p,q∈N*),则探究一探究二探究三当堂检测变式训练1(1)在等比数列{an}中,a1,a99是方程x2-10x+16=0的两个根,则a50的值为( )
A.10 B.16 C.±4 D.4
(2)在等比数列{an}中,a1a2=1,a5a6=9,则a3a4=( )解析:(1)依题意,得a1·a99=16,而a1·a99= ,所以a50=±4.
(2)在等比数列{an}中,a1a2=1,a5a6=9,
所以a1a2a5a6=9.又a3a4=a1a6=a2a5,所以(a3a4)2=9.又a3a4与a1a2的符号相同,故a3a4=3.
答案:(1)C (2)A探究一探究二探究三当堂检测等比数列的综合问题
例2有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数和第四个数的和是16,中间两个数的和是12.求这四个数.
分析:根据条件,用两个未知数表示这四个数.所以,当a=4,d=4时,所求四个数为0,4,8,16;
当a=9,d=-6时,所求四个数为15,9,3,1.
故所求四个数为0,4,8,16或15,9,3,1.探究一探究二探究三当堂检测探究一探究二探究三当堂检测探究一探究二探究三当堂检测延伸探究将本例中的条件改为“有四个实数,前三个数依次成等比数列,它们的积是-8,后三个数依次成等差数列,它们的积为-80”,再求这四个数.探究一探究二探究三当堂检测等比数列的实际应用
例3为了治理“沙尘暴”,西部某地区政府经过多年努力,到2016年底,将当地沙漠绿化了40%,从2017年开始,每年将出现这种现象:原有沙漠面积的12%被绿化,即改造为绿洲(被绿化的部分叫绿洲),同时原有绿洲面积的8%又被侵蚀为沙漠,问至少经过几年的绿化,才能使该地区的绿洲面积超过50%?(可参考数据lg 2≈0.3,最后结果精确到整数)
分析:依题意,每年的沙漠面积与绿洲面积之和是确定的,另外需根据题意建立前后两年绿洲面积之间的关系,由此构造等比数列解决问题.探究一探究二探究三当堂检测探究一探究二探究三当堂检测所以至少经过4年才能使该地区的绿洲面积超过50%.探究一探究二探究三当堂检测反思感悟1.一般地,涉及产值增长率问题、银行利息问题、细胞繁殖等实际问题时,往往与等比数列有关,可建立等比数列模型进行求解.
2.建立等比数列模型进行运算时,往往涉及指数、对数方程或不等式的问题,要注意运算的正确性,还要善于进行估算,对于近似计算问题,答案要符合实际问题的需要.探究一探究二探究三当堂检测变式训练2一种专门占据内存的计算机病毒开始时占据内存2 KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,那么开机后 分钟,该病毒占据内存64 MB(1 MB=210 KB).?
解析:由题意,得每3分钟病毒占的内存容量构成一个等比数列,设病毒占据64 MB时自身复制了n次,即2×2n=64×210=216,解得n=15,从而复制的时间为15×3=45(分钟).
答案:45探究一探究二探究三当堂检测1.对任意等比数列{an},下列说法一定正确的是( )
A.a1,a3,a9成等比数列 B.a2,a3,a6成等比数列
C.a2,a4,a8成等比数列 D.a3,a6,a9成等比数列
解析:根据等比数列的性质,若m+n=2k(m,n,k∈N*),则am,ak,an成等比数列.
即a3,a6,a9成等比数列.故选D.
答案:D
2.在等比数列{an}中,若a2=8,a5=64,则公比q为( )
A.2 B.3 C.4 D.8
解析:由a5=a2q3,得q3=8,所以q=2.
答案:A探究一探究二探究三当堂检测3.一张报纸的厚度为a,面积为b,现将此报纸对折(沿对边中点连线折叠)7次,这时报纸的厚度和面积分别为 ( )答案:C 探究一探究二探究三当堂检测4.在等比数列{an}中,a1+a2=30,a3+a4=120,则a5+a6= .?
解析:根据等比数列的性质可知a1+a2,a3+a4,a5+a6也成等比数列,即(a3+a4)2=(a1+a2)(a5+a6),答案:480 探究一探究二探究三当堂检测5.已知数列{an}为等比数列.
(1)若a1+a2+a3=21,a1a2a3=216,求an;
(2)若a3a5=18,a4a8=72,求公比q.
