高中数学 人教A版必修五课件 1章模块复习课 第1课时 解三角形 :42张PPT
文档属性
| 名称 | 高中数学 人教A版必修五课件 1章模块复习课 第1课时 解三角形 :42张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 13:30:56 | ||
图片预览










文档简介
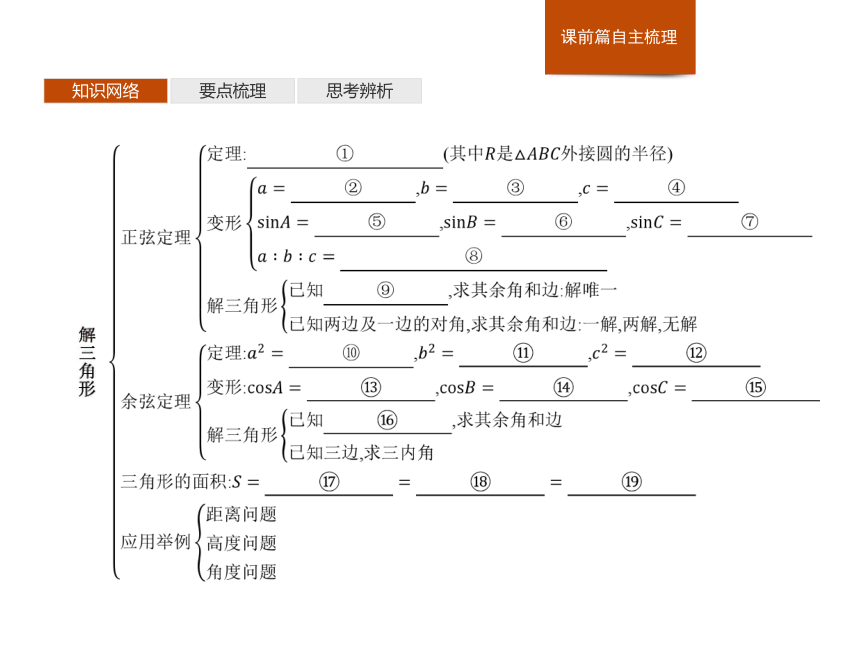
课件42张PPT。第1课时 解三角形知识网络要点梳理思考辨析知识网络要点梳理思考辨析知识网络要点梳理思考辨析1.正弦、余弦定理 知识网络要点梳理思考辨析2.利用正弦、余弦定理解三角形
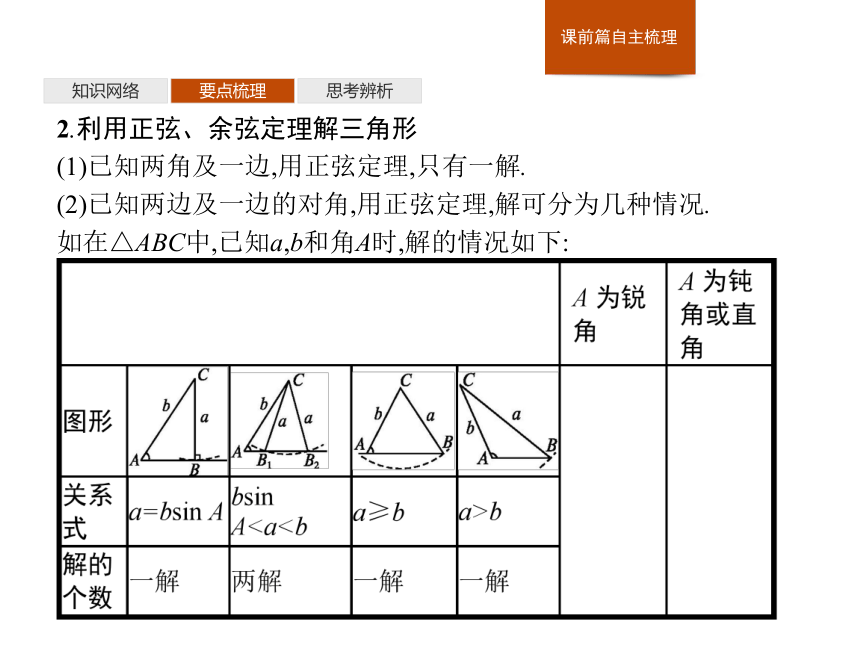
(1)已知两角及一边,用正弦定理,只有一解.
(2)已知两边及一边的对角,用正弦定理,解可分为几种情况.
如在△ABC中,已知a,b和角A时,解的情况如下:知识网络要点梳理思考辨析上表中,当角A为锐角时,a当角A为钝角或直角时,a=b,a(3)已知三边,用余弦定理,有解时,只有一解.
(4)已知两边及夹角,用余弦定理,必有一解.知识网络要点梳理思考辨析3.三角形的面积公式
设△ABC的三边分别为a,b,c,对应的三个内角分别为A,B,C,其面积为S.4.三角形中的一些重要结论
(1)A+B+C=π.
(2)在三角形中大边对大角,反之亦然.
(3)任意两边之和大于第三边,任意两边之差小于第三边.知识网络要点梳理思考辨析(4)三角形内的诱导公式: (5)在△ABC中,tan A+tan B+tan C=tan A·tan B·tan C.
(6)在△ABC中,角A,B,C成等差数列的充要条件是B=60°.
(7)△ABC为正三角形的充要条件是角A,B,C成等差数列,且a,b,c成等比数列.知识网络要点梳理思考辨析判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.答案:(1)× (2)√ (3)× (4)× (5)√ (6)× 专题归纳高考体验专题一 利用正弦、余弦定理解三角形 解析:先在△ABD中,利用正弦定理求得∠ADB,从而得到∠BAD,∠BAC,最后在△ABC中求得AC的值.
如图,在△ABD中,由正弦定理,专题归纳高考体验反思感悟解三角形的常见题型及求解方法 专题归纳高考体验专题归纳高考体验专题二 利用正弦、余弦定理判断三角形的形状
例2若△ABC的三个内角满足sin A∶sin B∶sin C=5∶11∶13,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形,也可能是钝角三角形专题归纳高考体验解析:先利用正弦定理将已知条件转化为三边的比值,再利用余弦定理求出最大角,即可作出判断.
在△ABC中,∵sin A∶sin B∶sin C=5∶11∶13,
∴a∶b∶c=5∶11∶13,
故令a=5k,b=11k,c=13k(k>0).由余弦定理可得∴△ABC为钝角三角形.
答案:C专题归纳高考体验反思感悟利用正弦、余弦定理判断三角形形状的基本方法
1.“角化边”:利用正弦、余弦定理把已知条件转化为只含边的关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
2.“边化角”:利用正弦、余弦定理把已知条件转化为只含内角的三角函数间的关系,通过三角恒等变换,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.专题归纳高考体验变式训练2已知△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
解析:∵由正弦定理得sin Bcos C+sin Ccos B=sin2A,
∴sin(B+C)=sin2A,
即sin(π-A)=sin2A,sin A=sin2A.
∵A∈(0,π),∴sin A>0,∴sin A=1,即A= ,故选B.
答案:B专题归纳高考体验专题三 利用正弦、余弦定理解决实际应用问题
例3已知海岛A四周8 n mile内有暗礁,有一货轮由西向东航行,望见岛A在北偏东75°的方向上,航行20 n mile后,见此岛在北偏东30°的方向上.若货轮不改变航向继续前进,有无触礁危险?专题归纳高考体验反思感悟解三角形应用题的常见情况及方法
1.实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
2.实际问题经抽象概括后,已知量与未知量涉及两个或两个以上的三角形,这时需作出这些三角形,先解条件足够的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.专题归纳高考体验变式训练3如图所示,某公园计划用鹅卵石铺成两条交叉的“健康石道”(线段AD和CE),并在这两条“健康石道”两端之间建设“花卉长廊”(线段AC和ED),以供市民休闲健身.已铺设好的部分BD=20 m,ED=10 m,∠BED=45°(△BDE为锐角三角形).由于设计要求,未铺设好的部分AB和BC的总长只能为40 m,则剩余的“花卉长廊”(线段AC)最短可以是 m.?专题归纳高考体验设AB=x m,则BC=(40-x)m,在△ABC中,由余弦定理,得AC2=AB2+BC2-2AB·BC·cos∠ABC,
∴AC2=x2+(40-x)2-x(40-x)=3x2-120x+1 600=3(x-20)2+400.
∴当x=20时,AC2取得最小值400,
∴AC的最小值为20.答案:20 专题归纳高考体验专题四 正弦、余弦定理和三角恒等变换的综合应用
例4在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=8.分析:(1)根据边长关系求解出c,再由余弦定理求解出cos C的值;(2)先运用二倍角公式对已知等式进行降次化简,再运用两角和公式得到sin A+sin B与sin C之间的等量关系,利用正弦定理和三角形的面积公式求解出a,b的值.专题归纳高考体验化简得sin A+sin Acos B+sin B+sin Bcos A=4sin C.
因为sin Acos B+cos Asin B=sin(A+B)=sin C,
所以sin A+sin B=3sin C.
由正弦定理可知a+b=3c.
又因为a+b+c=8,所以c=2,a+b=6.专题归纳高考体验反思感悟正弦、余弦定理常与三角恒等变换、三角形面积公式结合在一起综合考查学生的能力,解题的关键是结合条件,利用正弦、余弦定理进行边角互化,然后在此基础上进行三角恒等变换,解题时要注意公式的变形及熟练应用.专题归纳高考体验专题归纳高考体验考点一 正弦、余弦定理的基本应用 答案:A 专题归纳高考体验2.(2017·山东高考)在△ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则下列等式成立的是( )
A.a=2b B.b=2a
C.A=2B D.B=2A
解析:由题意可知sin B+2sin Bcos C=sin Acos C+sin(A+C),即2sin Bcos C=sin Acos C.因为cos C≠0,所以2sin B=sin A,由正弦定理可知a=2b.
答案:A专题归纳高考体验答案:C 专题归纳高考体验专题归纳高考体验专题归纳高考体验考点二 三角形面积的计算 答案:C 专题归纳高考体验专题归纳高考体验8.(2017·全国Ⅱ高考)△ABC的内角A,B,C的对边分别为a,b,c.已知sin(A+C)=8sin2 .
(1)求cos B;
(2)若a+c=6,△ABC的面积为2,求b.专题归纳高考体验专题归纳高考体验9.(2019·全国Ⅲ高考)△ABC的内角A,B,C的对边分别为a,b,c.已知 (1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.专题归纳高考体验专题归纳高考体验考点三 正弦、余弦定理的实际应用
10.(2015·湖北高考)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD= m.?专题归纳高考体验专题归纳高考体验考点四 正弦、余弦定理的综合应用 答案:A 专题归纳高考体验12.(2019·全国Ⅰ高考)△ABC的内角A,B,C的对边分别为a,b,c.设(sin B-sin C)2=sin2A-sin Bsin C.
(1)求A;专题归纳高考体验专题归纳高考体验13.(2018·全国Ⅰ高考)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;专题归纳高考体验14.(2017·全国Ⅰ高考)△ABC的内角A,B,C的对边分别为a,b,c.已知 (1)求sin Bsin C;
(2)若6cos Bcos C=1,a=3,求△ABC的周长.
(1)已知两角及一边,用正弦定理,只有一解.
(2)已知两边及一边的对角,用正弦定理,解可分为几种情况.
如在△ABC中,已知a,b和角A时,解的情况如下:知识网络要点梳理思考辨析上表中,当角A为锐角时,a
(4)已知两边及夹角,用余弦定理,必有一解.知识网络要点梳理思考辨析3.三角形的面积公式
设△ABC的三边分别为a,b,c,对应的三个内角分别为A,B,C,其面积为S.4.三角形中的一些重要结论
(1)A+B+C=π.
(2)在三角形中大边对大角,反之亦然.
(3)任意两边之和大于第三边,任意两边之差小于第三边.知识网络要点梳理思考辨析(4)三角形内的诱导公式: (5)在△ABC中,tan A+tan B+tan C=tan A·tan B·tan C.
(6)在△ABC中,角A,B,C成等差数列的充要条件是B=60°.
(7)△ABC为正三角形的充要条件是角A,B,C成等差数列,且a,b,c成等比数列.知识网络要点梳理思考辨析判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.答案:(1)× (2)√ (3)× (4)× (5)√ (6)× 专题归纳高考体验专题一 利用正弦、余弦定理解三角形 解析:先在△ABD中,利用正弦定理求得∠ADB,从而得到∠BAD,∠BAC,最后在△ABC中求得AC的值.
如图,在△ABD中,由正弦定理,专题归纳高考体验反思感悟解三角形的常见题型及求解方法 专题归纳高考体验专题归纳高考体验专题二 利用正弦、余弦定理判断三角形的形状
例2若△ABC的三个内角满足sin A∶sin B∶sin C=5∶11∶13,则△ABC( )
A.一定是锐角三角形
B.一定是直角三角形
C.一定是钝角三角形
D.可能是锐角三角形,也可能是钝角三角形专题归纳高考体验解析:先利用正弦定理将已知条件转化为三边的比值,再利用余弦定理求出最大角,即可作出判断.
在△ABC中,∵sin A∶sin B∶sin C=5∶11∶13,
∴a∶b∶c=5∶11∶13,
故令a=5k,b=11k,c=13k(k>0).由余弦定理可得∴△ABC为钝角三角形.
答案:C专题归纳高考体验反思感悟利用正弦、余弦定理判断三角形形状的基本方法
1.“角化边”:利用正弦、余弦定理把已知条件转化为只含边的关系,通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
2.“边化角”:利用正弦、余弦定理把已知条件转化为只含内角的三角函数间的关系,通过三角恒等变换,得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.专题归纳高考体验变式训练2已知△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不确定
解析:∵由正弦定理得sin Bcos C+sin Ccos B=sin2A,
∴sin(B+C)=sin2A,
即sin(π-A)=sin2A,sin A=sin2A.
∵A∈(0,π),∴sin A>0,∴sin A=1,即A= ,故选B.
答案:B专题归纳高考体验专题三 利用正弦、余弦定理解决实际应用问题
例3已知海岛A四周8 n mile内有暗礁,有一货轮由西向东航行,望见岛A在北偏东75°的方向上,航行20 n mile后,见此岛在北偏东30°的方向上.若货轮不改变航向继续前进,有无触礁危险?专题归纳高考体验反思感悟解三角形应用题的常见情况及方法
1.实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.
2.实际问题经抽象概括后,已知量与未知量涉及两个或两个以上的三角形,这时需作出这些三角形,先解条件足够的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.专题归纳高考体验变式训练3如图所示,某公园计划用鹅卵石铺成两条交叉的“健康石道”(线段AD和CE),并在这两条“健康石道”两端之间建设“花卉长廊”(线段AC和ED),以供市民休闲健身.已铺设好的部分BD=20 m,ED=10 m,∠BED=45°(△BDE为锐角三角形).由于设计要求,未铺设好的部分AB和BC的总长只能为40 m,则剩余的“花卉长廊”(线段AC)最短可以是 m.?专题归纳高考体验设AB=x m,则BC=(40-x)m,在△ABC中,由余弦定理,得AC2=AB2+BC2-2AB·BC·cos∠ABC,
∴AC2=x2+(40-x)2-x(40-x)=3x2-120x+1 600=3(x-20)2+400.
∴当x=20时,AC2取得最小值400,
∴AC的最小值为20.答案:20 专题归纳高考体验专题四 正弦、余弦定理和三角恒等变换的综合应用
例4在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=8.分析:(1)根据边长关系求解出c,再由余弦定理求解出cos C的值;(2)先运用二倍角公式对已知等式进行降次化简,再运用两角和公式得到sin A+sin B与sin C之间的等量关系,利用正弦定理和三角形的面积公式求解出a,b的值.专题归纳高考体验化简得sin A+sin Acos B+sin B+sin Bcos A=4sin C.
因为sin Acos B+cos Asin B=sin(A+B)=sin C,
所以sin A+sin B=3sin C.
由正弦定理可知a+b=3c.
又因为a+b+c=8,所以c=2,a+b=6.专题归纳高考体验反思感悟正弦、余弦定理常与三角恒等变换、三角形面积公式结合在一起综合考查学生的能力,解题的关键是结合条件,利用正弦、余弦定理进行边角互化,然后在此基础上进行三角恒等变换,解题时要注意公式的变形及熟练应用.专题归纳高考体验专题归纳高考体验考点一 正弦、余弦定理的基本应用 答案:A 专题归纳高考体验2.(2017·山东高考)在△ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sin B(1+2cos C)=2sin Acos C+cos Asin C,则下列等式成立的是( )
A.a=2b B.b=2a
C.A=2B D.B=2A
解析:由题意可知sin B+2sin Bcos C=sin Acos C+sin(A+C),即2sin Bcos C=sin Acos C.因为cos C≠0,所以2sin B=sin A,由正弦定理可知a=2b.
答案:A专题归纳高考体验答案:C 专题归纳高考体验专题归纳高考体验专题归纳高考体验考点二 三角形面积的计算 答案:C 专题归纳高考体验专题归纳高考体验8.(2017·全国Ⅱ高考)△ABC的内角A,B,C的对边分别为a,b,c.已知sin(A+C)=8sin2 .
(1)求cos B;
(2)若a+c=6,△ABC的面积为2,求b.专题归纳高考体验专题归纳高考体验9.(2019·全国Ⅲ高考)△ABC的内角A,B,C的对边分别为a,b,c.已知 (1)求B;
(2)若△ABC为锐角三角形,且c=1,求△ABC面积的取值范围.专题归纳高考体验专题归纳高考体验考点三 正弦、余弦定理的实际应用
10.(2015·湖北高考)如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD= m.?专题归纳高考体验专题归纳高考体验考点四 正弦、余弦定理的综合应用 答案:A 专题归纳高考体验12.(2019·全国Ⅰ高考)△ABC的内角A,B,C的对边分别为a,b,c.设(sin B-sin C)2=sin2A-sin Bsin C.
(1)求A;专题归纳高考体验专题归纳高考体验13.(2018·全国Ⅰ高考)在平面四边形ABCD中,∠ADC=90°,∠A=45°,AB=2,BD=5.
(1)求cos∠ADB;专题归纳高考体验14.(2017·全国Ⅰ高考)△ABC的内角A,B,C的对边分别为a,b,c.已知 (1)求sin Bsin C;
(2)若6cos Bcos C=1,a=3,求△ABC的周长.
