鲁教版(五四制)八年级上册 第四章 图形的平移与旋转 巩固练习(解析版)
文档属性
| 名称 | 鲁教版(五四制)八年级上册 第四章 图形的平移与旋转 巩固练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 278.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-19 10:13:58 | ||
图片预览


文档简介
鲁教版数学-八年级上册-第四章-图形的平移与旋转-巩固练习
一、单选题
1.如图,在△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为(?? )
A.?(﹣1,﹣ )????????????????????????????????????????????????B.?(﹣1,﹣ )或(﹣2,0) C.?(﹣ ,1)或(0,﹣2)??????????????????????????????D.?(﹣ ,1)
2.如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
A.?平移一次形成的??????????????????????????????????????????????????
B.?平移两次形成的 C.?以轴心为旋转中心,旋转120°后形成的??????????????
D.?以轴心为旋转中心,旋转120°、240°后形成的
3.点M(﹣3,﹣5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为( )
A.?(0,﹣9)?????????????????????B.?(﹣6,﹣1)?????????????????????C.?(1,﹣2)?????????????????????D.?(1,﹣8)
4.如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2 个单位长度到点O2 , 点A的位置不变,如果以O2为原点,那么点A的坐标可能是(?? )
A.?(3,﹣1)??????????????B.?(1,﹣3)??????????????C.?(﹣2,﹣1)??????????????D.?(2 +1,2 +1)
5.用放大镜将图形放大,应该属于( )
A.?平移变换???????????????B.?相似变换???????????????????????????C.?对称变换???????????????????????????D.?旋转变换
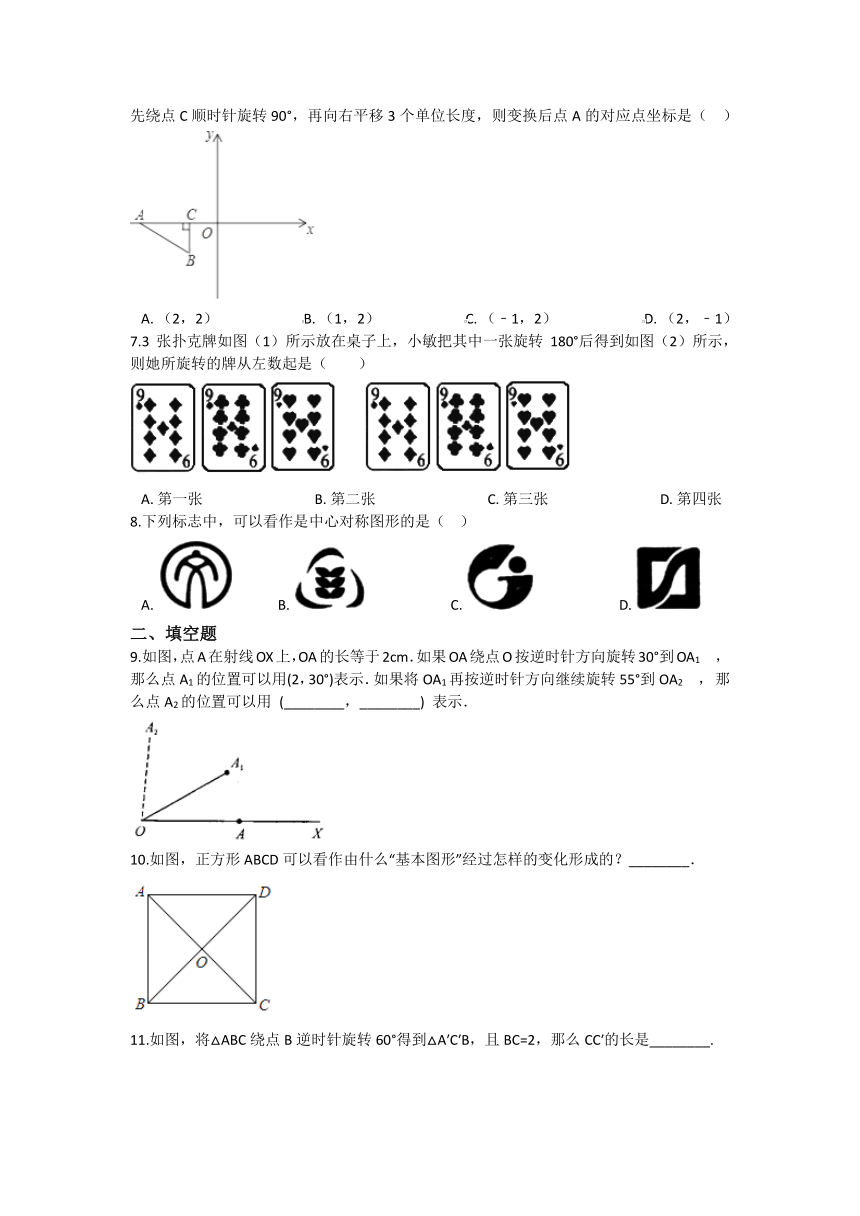
6.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是(?? )
A.?(2,2)????????????????????????B.?(1,2)????????????????????????C.?(﹣1,2)????????????????????????D.?(2,﹣1)
7.3张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到如图(2)所示,则她所旋转的牌从左数起是( )
A.?第一张????????????????????????????????B.?第二张????????????????????????????????C.?第三张????????????????????????????????D.?第四张
8.下列标志中,可以看作是中心对称图形的是(?? )
A.??????????????B.??????????????????????????C.??????????????????????????D.?
二、填空题
9.如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA1 , 那么点A1的位置可以用(2,30°)表示.如果将OA1再按逆时针方向继续旋转55°到OA2 , 那么点A2的位置可以用 (________,________) 表示.
10.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________.
11.如图,将△ABC绕点B逆时针旋转60°得到△A′C′B,且BC=2,那么CC′的长是________.
12.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1 , 点P1绕点B旋转180°得到点P2 , 点P2绕点C旋转180°得到点P3 , 点P3绕点A旋转180°得到点P4 , …,按此作法进行下去,则点P2018的坐标为________.
13.已知点A(2a+3b,﹣2)和点B(8,3a+2b)关于原点对称,则a+b=________?.
14.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为________.
?
15.如图,将三角形ABC沿直线AB的方向向右平移至三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为________
16.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为________,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为________.
三、解答题
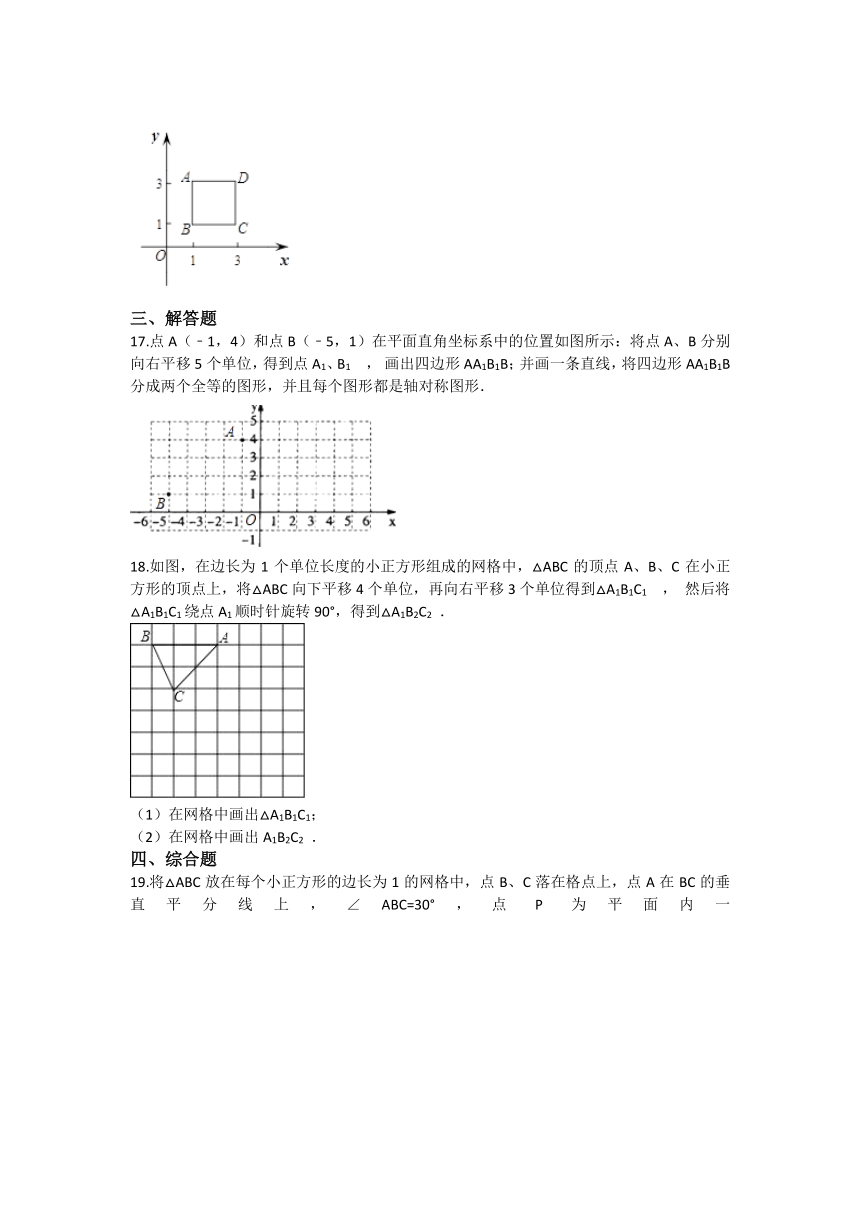
17.点A(﹣1,4)和点B(﹣5,1)在平面直角坐标系中的位置如图所示:将点A、B分别向右平移5个单位,得到点A1、B1 , 画出四边形AA1B1B;并画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2 .
(1)在网格中画出△A1B1C1;
(2)在网格中画出A1B2C2 .
四、综合题
19.将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB=________度;
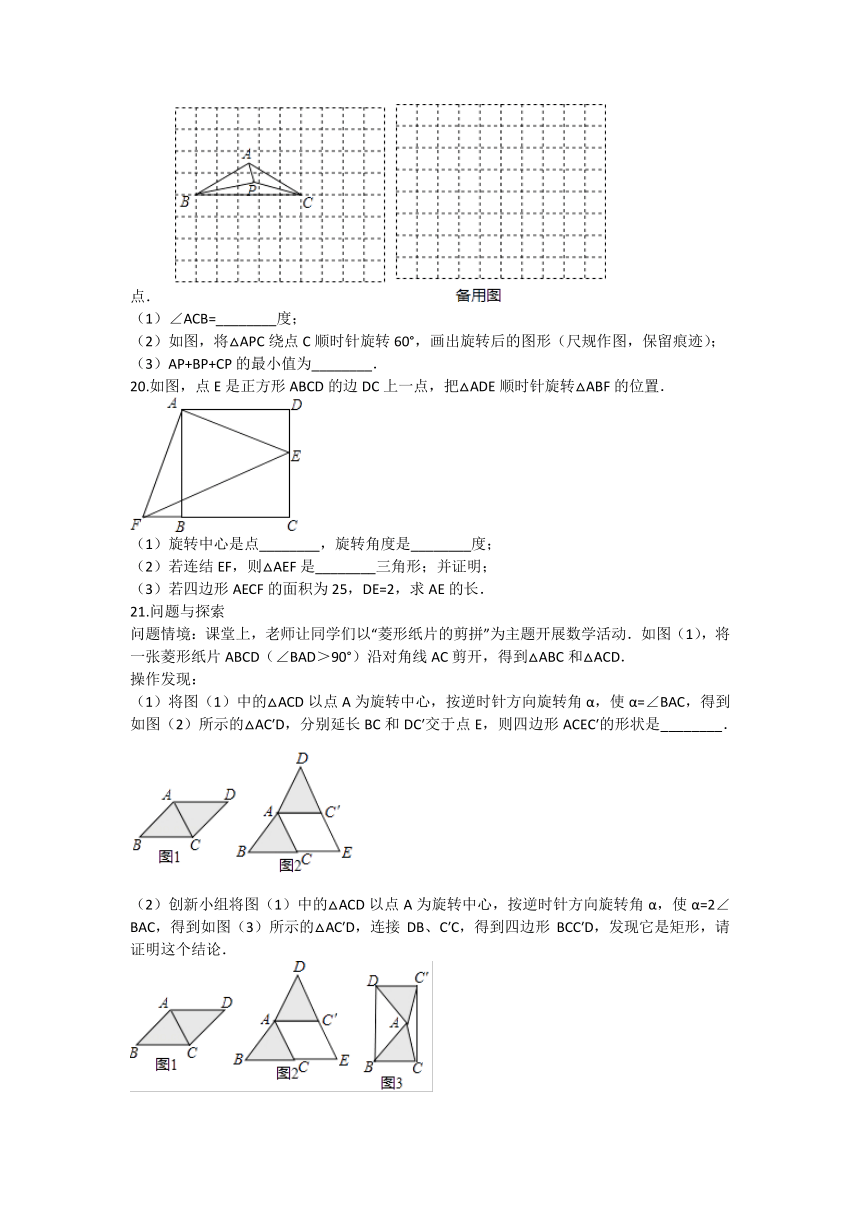
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为________.
20.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点________,旋转角度是________度;
(2)若连结EF,则△AEF是________三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
21.问题与探索 问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD. 操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是________.
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
答案
一、单选题
1.【答案】 B
【解析】【解答】解:∵△ABO中,AB⊥OB,OB= ,AB=1,
∴tan∠AOB= = ,
∴∠AOB=30°.
如图1,当△ABO绕点O顺时针旋转150°后得到△A1B1O,
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°,
则易求A1(﹣1,﹣ );
如图2,当△ABO绕点O逆时针旋转150°后得到△A1B1O,
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°,
则易求A1(﹣2,0);
综上所述,点A1的坐标为(﹣1,﹣ )或(﹣2,0).
故选:B.
【分析】需要分类讨论:在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标.
2.【答案】 D
【解析】【解答】解:如图所示:∵旋转中心的旋转角360°,
∴每个图形旋转的角度为:360°÷3=120°,
∴把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”:以轴心为旋转中心,旋转120°、240°后形成的.
故答案为:D
【分析】根据图形,由一个基本图形旋转后得到了三个基本图形,因为旋转中心的旋转角360°,所以可以用360°,除以3即可得到每个图形旋转的角度.
3.【答案】 A
【解析】【解答】解:点M(﹣3,﹣5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为(﹣3+3,﹣5﹣4),
即(0,﹣9),
故选:A.
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减进行计算即可.
4.【答案】A
【解析】【解答】解:如图, 由题意,可得O1M=O1N=1. ∵将点O1平移2 个单位长度到点O2 , ∴O1O2=2 ,O1P=O2P=2, ∴PM=3, ∴点A的坐标是(3,﹣1). 故选A. 【分析】根据题意画出图形,利用平移的特征结合图形即可求解.
5.【答案】 B
【解析】【解答】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.
故选:B.
【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.
6.【答案】A
【解析】【解答】解:∵点C的坐标为(﹣1,0),AC=2,
∴点A的坐标为(﹣3,0),
如图所示,
将Rt△ABC先绕点C顺时针旋转90°,则点A′的坐标为(﹣1,2),
再向右平移3个单位长度,则变换后点A′的对应点坐标为(2,2),故答案为:A.
【分析】将Rt△ABC先绕点C顺时针旋转90°,画出图形,根据点C的坐标为(﹣1,0),AC=2,就可得出点A的坐标及点A′的坐标,再根据平移的性质求出结果。
7.【答案】 A
【解析】【分析】旋转前后图形的形状一样,从而可判断旋转的那一张牌是中心对称图形,由此可得出答案.
【解答】旋转前后图形的形状一样, 图1中从左边数第二、三张扑克牌旋转180度后,图形不能和原来的图形重合,而第一张旋转180度后正好与原图重合. 故选A.
【点评】本题考查的是中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
8.【答案】 D
【解析】【解答】解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、是中心对称图形,故本选项正确;
故选D.
【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.
二、填空题
9.【答案】 2;85
【解析】【解答】解:根据旋转的定义,可得出A2的位置可表示为(2,85) 故答案为:2;85. 【分析】根据旋转的定义可求解。
10.【答案】把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
【解析】【解答】观察图形可知把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.故答案为:把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD 【分析】旋转的性质:①旋转后的每一点都绕着旋转中心,旋转了同样大小的角度;②旋转后的图形与原来图形的形状与大小都没有发生变化,③旋转前后两个图形的对应点到旋转中心的距离相等;④对应点到旋转中心的连线所成的角相等.观察图形,回想正方形的特性; 根据旋转变换图形的性质即可得出答案.
11.【答案】2
【解析】【解答】∵△ABC绕点B逆时针旋转60°得到△A′C′B,
∴BC=BC′=2,∠CBC′=60°,
∴△BCC′为等边三角形,
∴CC′=BC=BC′=2.
故答案为:2
【分析】根据旋转的性质可得BC=BC′=2,∠CBC′=60°可得△BCC′为等边三角形,从而求得CC′的长。
12.【答案】 (2,-4)
【解析】【解答】解:如图所示,
P1(﹣2,0),P2(2,﹣4),P3(0,4),P4(﹣2,﹣2),P5(2,﹣2),P6(0,2), 发现6次一个循环.∵2018÷6=336…2, ∴点P2018的坐标与P2的坐标相同,即P2017(2,﹣4). 故答案为:(2,﹣4).
【分析】利用旋转的性质,画出P1 , P2 , P3 , P4 , …,再写出点 P1 , P2 , P3 , P4 , P5 , P6…,的坐标,再寻找规律,发现6次一个循环,因此用2018÷6,根据余数可得出点P2018的坐标。
13.【答案】
【解析】【解答】解:由题意得:, 解得, a+b=2﹣=, 故答案为:. 【分析】根据两个点关于原点对称时,它们的坐标符号相反可得,解方程组可得a、b的值,进而可计算出a+b的值.
14.【答案】
【解析】【解答】∵ 等边△ABC中,D是BC中点, ∴BD=3,AD⊥BC,∠BAD=∠CAD=30°, AD= , 又△ABD绕点A旋转后得到△ACE, ∴∠CAE=30°,∠DAE=60°,AD=AE, ∴△ADE是等边三角形, ∴DE=AD= 。 故答案为: 。 【分析】由等边三角形的性质可求得AD长,再根据旋转可知AD=AE,∠DAE=60°,△ADE为等边三角形,即可求出DE长。
15.【答案】30°
【解析】【解答】解:由平移的性质知,∠CAB=∠EBD=50°,又∠ABC=100°,所以∠CBE=180°-∠ABC-∠EBD=180°-100°-50°=30°. 故答案为:30° 【分析】因为平移后的图形与原图形对应角相等,所以∠EBD=∠CAB=,利用平角的特征,可求出∠CBE的值.
16.【答案】(-1,-3);(-3,-3)
【解析】【解答】一次变换实际上就是做了中心对称,两次变换后回到原来的位置.则一次变换后A的坐标为(-1,-3);经过2015次变换后点D的坐标为(-3,-3) 故答案为:(-1,-3)(-3,-3) 【分析】本题看似复杂,实则在考查中心对称的特征,根据题意作图不难求解.
三、解答题
17.【答案】 解:所作图形如下:
【解析】【分析】(1)将点A、B分别向右平移5个单位,得到点A1、B1 , 顺次连接四点即可.(2)取AB1或,A1B即可.
18.【答案】(1)解:如图所示:△A1B1C1 , 即为所求。
(2)解:如图所示:△A2B2C2 , 即为所求。
【解析】【分析】(1)先将三角形的各个点下移四个单位,再右移三个单位,找到对应的点,相连得到三角形; (2)在(1)的基础上,再绕A1旋转90度,找到各个旋转后的点,相连得三角形。
四、综合题
19.【答案】(1)30° (2)解:如图△CA′P′就是所求的三角形 (3)
【解析】【解答】解(1)∵点A在BC的垂直平分线上. ∴AB=AC, ∴∠ABC=∠ACB, ∵∠ABC=30°, ∴∠ACB=30°. 故答案为30°. (2.)如图△CA′P′就是所求的三角形. (3.)如图当B、P、P′、A′共线时,PA+PB+PC=PB+PP′+P′A的值最小, 此时BC=5,AC=CA′= ,BA′= = . 故答案为 . 【分析】(1)根据垂直平分线的性质即可解决问题.(2)根据中心旋转的定义即可画出图形.(3)根据两点之间线段最短即可解决问题.
20.【答案】 (1)A;90 (2)等腰直角 (3)解:由题意得:△ADE≌△ABF,
∴S四边形AECF=S正方形ABCD=25,
∴AD=5,而∠D=90°,DE=2,
∴ .
【解析】【解答】解:(1)如图,由题意得:
旋转中心是点A,旋转角度是90度.
故答案为A、90.(2)由题意得:AF=AE,∠EAF=90°,
∴△AEF为等腰直角三角形.
故答案为等腰直角.
【分析】(1)根据旋转变换的定义,即可解决问题.(2)根据旋转变换的定义,即可解决问题.(3)根据旋转变换的定义得到△ADE≌△ABF,进而得到S四边形AECF=S正方形ABCD=25,求出AD的长度,即可解决问题.
21.【答案】(1)菱形 (2)解:如图3中,过点A作AE⊥C′C于点E, 由旋转的性质,得AC′=AC, ∴∠CAE=∠C′AE= α=∠ABC,∠AEC=90°, ∵BA=BC, ∴∠BCA=∠BAC ∴∠CAE=∠BCA, ∴AE∥BC. 同理,AE∥DC′, ∴BC∥DC′, 又∵BC=DC′, ∴四边形BCC′D是平行四边形, 又∵AE∥BC,∠AEC=90°, ∴∠BCC′=1800﹣900=900 ∴四边形BCC′D是矩形
【解析】【解答】解:(1)结论:菱形. 理由:如图2中, 由题意∵AB=BC, ∴∠BAC=∠BCA=∠CAC′=∠AC′D ∴AC′∥EC, ∵∠CAC′=∠AC′D, ∴AC∥EC′, ∴四边形ACEC′是平行四边形, ∵AC=AC′, ∴四边形ACEC′是菱形. 【分析】(1)结论:菱形.首先证明四边形ACEC′是平行四边形,再由AC=AC′即可证明结论.(2)如图3中,过点A作AE⊥C′C于点E,首先证明DC′∥CB,DC′=BC,推出四边形BCC′D是平行四边形,再证明∠BCC′=900即可.
一、单选题
1.如图,在△ABO中,AB⊥OB,OB= ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为(?? )
A.?(﹣1,﹣ )????????????????????????????????????????????????B.?(﹣1,﹣ )或(﹣2,0) C.?(﹣ ,1)或(0,﹣2)??????????????????????????????D.?(﹣ ,1)
2.如图是由三把相同大小的扇子展开后组成的图形,若把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”( )
A.?平移一次形成的??????????????????????????????????????????????????
B.?平移两次形成的 C.?以轴心为旋转中心,旋转120°后形成的??????????????
D.?以轴心为旋转中心,旋转120°、240°后形成的
3.点M(﹣3,﹣5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为( )
A.?(0,﹣9)?????????????????????B.?(﹣6,﹣1)?????????????????????C.?(1,﹣2)?????????????????????D.?(1,﹣8)
4.如图,直线m⊥n.在平面直角坐标系xOy中,x轴∥m,y轴∥n.如果以O1为原点,点A 的坐标为(1,1).将点O1平移2 个单位长度到点O2 , 点A的位置不变,如果以O2为原点,那么点A的坐标可能是(?? )
A.?(3,﹣1)??????????????B.?(1,﹣3)??????????????C.?(﹣2,﹣1)??????????????D.?(2 +1,2 +1)
5.用放大镜将图形放大,应该属于( )
A.?平移变换???????????????B.?相似变换???????????????????????????C.?对称变换???????????????????????????D.?旋转变换
6.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(﹣1,0),AC=2.将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点坐标是(?? )
A.?(2,2)????????????????????????B.?(1,2)????????????????????????C.?(﹣1,2)????????????????????????D.?(2,﹣1)
7.3张扑克牌如图(1)所示放在桌子上,小敏把其中一张旋转180°后得到如图(2)所示,则她所旋转的牌从左数起是( )
A.?第一张????????????????????????????????B.?第二张????????????????????????????????C.?第三张????????????????????????????????D.?第四张
8.下列标志中,可以看作是中心对称图形的是(?? )
A.??????????????B.??????????????????????????C.??????????????????????????D.?
二、填空题
9.如图,点A在射线OX上,OA的长等于2cm.如果OA绕点O按逆时针方向旋转30°到OA1 , 那么点A1的位置可以用(2,30°)表示.如果将OA1再按逆时针方向继续旋转55°到OA2 , 那么点A2的位置可以用 (________,________) 表示.
10.如图,正方形ABCD可以看作由什么“基本图形”经过怎样的变化形成的?________.
11.如图,将△ABC绕点B逆时针旋转60°得到△A′C′B,且BC=2,那么CC′的长是________.
12.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(﹣1,1),B(0,﹣2),C(1,0),点P(0,2)绕点A旋转180°得到点P1 , 点P1绕点B旋转180°得到点P2 , 点P2绕点C旋转180°得到点P3 , 点P3绕点A旋转180°得到点P4 , …,按此作法进行下去,则点P2018的坐标为________.
13.已知点A(2a+3b,﹣2)和点B(8,3a+2b)关于原点对称,则a+b=________?.
14.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为________.
?
15.如图,将三角形ABC沿直线AB的方向向右平移至三角形BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为________
16.规定:在平面直角坐标系xOy中,“把某一图形先沿x轴翻折,再沿y轴翻折”为一次变化.如图,已知正方形ABCD,顶点A(1,3),C(3,1).若正方形ABCD经过一次上述变化,则点A变化后的坐标为________,如此这样,对正方形ABCD连续做2015次这样的变化,则点D变化后的坐标为________.
三、解答题
17.点A(﹣1,4)和点B(﹣5,1)在平面直角坐标系中的位置如图所示:将点A、B分别向右平移5个单位,得到点A1、B1 , 画出四边形AA1B1B;并画一条直线,将四边形AA1B1B分成两个全等的图形,并且每个图形都是轴对称图形.
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位,再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°,得到△A1B2C2 .
(1)在网格中画出△A1B1C1;
(2)在网格中画出A1B2C2 .
四、综合题
19.将△ABC放在每个小正方形的边长为1的网格中,点B、C落在格点上,点A在BC的垂直平分线上,∠ABC=30°,点P为平面内一点.
(1)∠ACB=________度;
(2)如图,将△APC绕点C顺时针旋转60°,画出旋转后的图形(尺规作图,保留痕迹);
(3)AP+BP+CP的最小值为________.
20.如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点________,旋转角度是________度;
(2)若连结EF,则△AEF是________三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
21.问题与探索 问题情境:课堂上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图(1),将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD. 操作发现:
(1)将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图(2)所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是________.
(2)创新小组将图(1)中的△ACD以点A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图(3)所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形,请证明这个结论.
答案
一、单选题
1.【答案】 B
【解析】【解答】解:∵△ABO中,AB⊥OB,OB= ,AB=1,
∴tan∠AOB= = ,
∴∠AOB=30°.
如图1,当△ABO绕点O顺时针旋转150°后得到△A1B1O,
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°,
则易求A1(﹣1,﹣ );
如图2,当△ABO绕点O逆时针旋转150°后得到△A1B1O,
则∠A1OC=150°﹣∠AOB﹣∠BOC=150°﹣30°﹣90°=30°,
则易求A1(﹣2,0);
综上所述,点A1的坐标为(﹣1,﹣ )或(﹣2,0).
故选:B.
【分析】需要分类讨论:在把△ABO绕点O顺时针旋转150°和逆时针旋转150°后得到△A1B1O时点A1的坐标.
2.【答案】 D
【解析】【解答】解:如图所示:∵旋转中心的旋转角360°,
∴每个图形旋转的角度为:360°÷3=120°,
∴把每把扇子的展开图看着“基本图案”那么该图形是由“基本图案”:以轴心为旋转中心,旋转120°、240°后形成的.
故答案为:D
【分析】根据图形,由一个基本图形旋转后得到了三个基本图形,因为旋转中心的旋转角360°,所以可以用360°,除以3即可得到每个图形旋转的角度.
3.【答案】 A
【解析】【解答】解:点M(﹣3,﹣5)是由N先向上平移4个单位,再向左平移3个单位而得到,则点N的坐标为(﹣3+3,﹣5﹣4),
即(0,﹣9),
故选:A.
【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减进行计算即可.
4.【答案】A
【解析】【解答】解:如图, 由题意,可得O1M=O1N=1. ∵将点O1平移2 个单位长度到点O2 , ∴O1O2=2 ,O1P=O2P=2, ∴PM=3, ∴点A的坐标是(3,﹣1). 故选A. 【分析】根据题意画出图形,利用平移的特征结合图形即可求解.
5.【答案】 B
【解析】【解答】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.
故选:B.
【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.
6.【答案】A
【解析】【解答】解:∵点C的坐标为(﹣1,0),AC=2,
∴点A的坐标为(﹣3,0),
如图所示,
将Rt△ABC先绕点C顺时针旋转90°,则点A′的坐标为(﹣1,2),
再向右平移3个单位长度,则变换后点A′的对应点坐标为(2,2),故答案为:A.
【分析】将Rt△ABC先绕点C顺时针旋转90°,画出图形,根据点C的坐标为(﹣1,0),AC=2,就可得出点A的坐标及点A′的坐标,再根据平移的性质求出结果。
7.【答案】 A
【解析】【分析】旋转前后图形的形状一样,从而可判断旋转的那一张牌是中心对称图形,由此可得出答案.
【解答】旋转前后图形的形状一样, 图1中从左边数第二、三张扑克牌旋转180度后,图形不能和原来的图形重合,而第一张旋转180度后正好与原图重合. 故选A.
【点评】本题考查的是中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.
8.【答案】 D
【解析】【解答】解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、是中心对称图形,故本选项正确;
故选D.
【分析】根据中心对称图形的定义,结合选项所给图形进行判断即可.
二、填空题
9.【答案】 2;85
【解析】【解答】解:根据旋转的定义,可得出A2的位置可表示为(2,85) 故答案为:2;85. 【分析】根据旋转的定义可求解。
10.【答案】把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD
【解析】【解答】观察图形可知把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD.故答案为:把△ABO绕O点连续旋转90°,180°,270°可以得到正方形ABCD 【分析】旋转的性质:①旋转后的每一点都绕着旋转中心,旋转了同样大小的角度;②旋转后的图形与原来图形的形状与大小都没有发生变化,③旋转前后两个图形的对应点到旋转中心的距离相等;④对应点到旋转中心的连线所成的角相等.观察图形,回想正方形的特性; 根据旋转变换图形的性质即可得出答案.
11.【答案】2
【解析】【解答】∵△ABC绕点B逆时针旋转60°得到△A′C′B,
∴BC=BC′=2,∠CBC′=60°,
∴△BCC′为等边三角形,
∴CC′=BC=BC′=2.
故答案为:2
【分析】根据旋转的性质可得BC=BC′=2,∠CBC′=60°可得△BCC′为等边三角形,从而求得CC′的长。
12.【答案】 (2,-4)
【解析】【解答】解:如图所示,
P1(﹣2,0),P2(2,﹣4),P3(0,4),P4(﹣2,﹣2),P5(2,﹣2),P6(0,2), 发现6次一个循环.∵2018÷6=336…2, ∴点P2018的坐标与P2的坐标相同,即P2017(2,﹣4). 故答案为:(2,﹣4).
【分析】利用旋转的性质,画出P1 , P2 , P3 , P4 , …,再写出点 P1 , P2 , P3 , P4 , P5 , P6…,的坐标,再寻找规律,发现6次一个循环,因此用2018÷6,根据余数可得出点P2018的坐标。
13.【答案】
【解析】【解答】解:由题意得:, 解得, a+b=2﹣=, 故答案为:. 【分析】根据两个点关于原点对称时,它们的坐标符号相反可得,解方程组可得a、b的值,进而可计算出a+b的值.
14.【答案】
【解析】【解答】∵ 等边△ABC中,D是BC中点, ∴BD=3,AD⊥BC,∠BAD=∠CAD=30°, AD= , 又△ABD绕点A旋转后得到△ACE, ∴∠CAE=30°,∠DAE=60°,AD=AE, ∴△ADE是等边三角形, ∴DE=AD= 。 故答案为: 。 【分析】由等边三角形的性质可求得AD长,再根据旋转可知AD=AE,∠DAE=60°,△ADE为等边三角形,即可求出DE长。
15.【答案】30°
【解析】【解答】解:由平移的性质知,∠CAB=∠EBD=50°,又∠ABC=100°,所以∠CBE=180°-∠ABC-∠EBD=180°-100°-50°=30°. 故答案为:30° 【分析】因为平移后的图形与原图形对应角相等,所以∠EBD=∠CAB=,利用平角的特征,可求出∠CBE的值.
16.【答案】(-1,-3);(-3,-3)
【解析】【解答】一次变换实际上就是做了中心对称,两次变换后回到原来的位置.则一次变换后A的坐标为(-1,-3);经过2015次变换后点D的坐标为(-3,-3) 故答案为:(-1,-3)(-3,-3) 【分析】本题看似复杂,实则在考查中心对称的特征,根据题意作图不难求解.
三、解答题
17.【答案】 解:所作图形如下:
【解析】【分析】(1)将点A、B分别向右平移5个单位,得到点A1、B1 , 顺次连接四点即可.(2)取AB1或,A1B即可.
18.【答案】(1)解:如图所示:△A1B1C1 , 即为所求。
(2)解:如图所示:△A2B2C2 , 即为所求。
【解析】【分析】(1)先将三角形的各个点下移四个单位,再右移三个单位,找到对应的点,相连得到三角形; (2)在(1)的基础上,再绕A1旋转90度,找到各个旋转后的点,相连得三角形。
四、综合题
19.【答案】(1)30° (2)解:如图△CA′P′就是所求的三角形 (3)
【解析】【解答】解(1)∵点A在BC的垂直平分线上. ∴AB=AC, ∴∠ABC=∠ACB, ∵∠ABC=30°, ∴∠ACB=30°. 故答案为30°. (2.)如图△CA′P′就是所求的三角形. (3.)如图当B、P、P′、A′共线时,PA+PB+PC=PB+PP′+P′A的值最小, 此时BC=5,AC=CA′= ,BA′= = . 故答案为 . 【分析】(1)根据垂直平分线的性质即可解决问题.(2)根据中心旋转的定义即可画出图形.(3)根据两点之间线段最短即可解决问题.
20.【答案】 (1)A;90 (2)等腰直角 (3)解:由题意得:△ADE≌△ABF,
∴S四边形AECF=S正方形ABCD=25,
∴AD=5,而∠D=90°,DE=2,
∴ .
【解析】【解答】解:(1)如图,由题意得:
旋转中心是点A,旋转角度是90度.
故答案为A、90.(2)由题意得:AF=AE,∠EAF=90°,
∴△AEF为等腰直角三角形.
故答案为等腰直角.
【分析】(1)根据旋转变换的定义,即可解决问题.(2)根据旋转变换的定义,即可解决问题.(3)根据旋转变换的定义得到△ADE≌△ABF,进而得到S四边形AECF=S正方形ABCD=25,求出AD的长度,即可解决问题.
21.【答案】(1)菱形 (2)解:如图3中,过点A作AE⊥C′C于点E, 由旋转的性质,得AC′=AC, ∴∠CAE=∠C′AE= α=∠ABC,∠AEC=90°, ∵BA=BC, ∴∠BCA=∠BAC ∴∠CAE=∠BCA, ∴AE∥BC. 同理,AE∥DC′, ∴BC∥DC′, 又∵BC=DC′, ∴四边形BCC′D是平行四边形, 又∵AE∥BC,∠AEC=90°, ∴∠BCC′=1800﹣900=900 ∴四边形BCC′D是矩形
【解析】【解答】解:(1)结论:菱形. 理由:如图2中, 由题意∵AB=BC, ∴∠BAC=∠BCA=∠CAC′=∠AC′D ∴AC′∥EC, ∵∠CAC′=∠AC′D, ∴AC∥EC′, ∴四边形ACEC′是平行四边形, ∵AC=AC′, ∴四边形ACEC′是菱形. 【分析】(1)结论:菱形.首先证明四边形ACEC′是平行四边形,再由AC=AC′即可证明结论.(2)如图3中,过点A作AE⊥C′C于点E,首先证明DC′∥CB,DC′=BC,推出四边形BCC′D是平行四边形,再证明∠BCC′=900即可.
