人教版八年级数学上册课件:14.2.2 完全平方公式(20张PPT)
文档属性
| 名称 | 人教版八年级数学上册课件:14.2.2 完全平方公式(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-19 00:00:00 | ||
图片预览


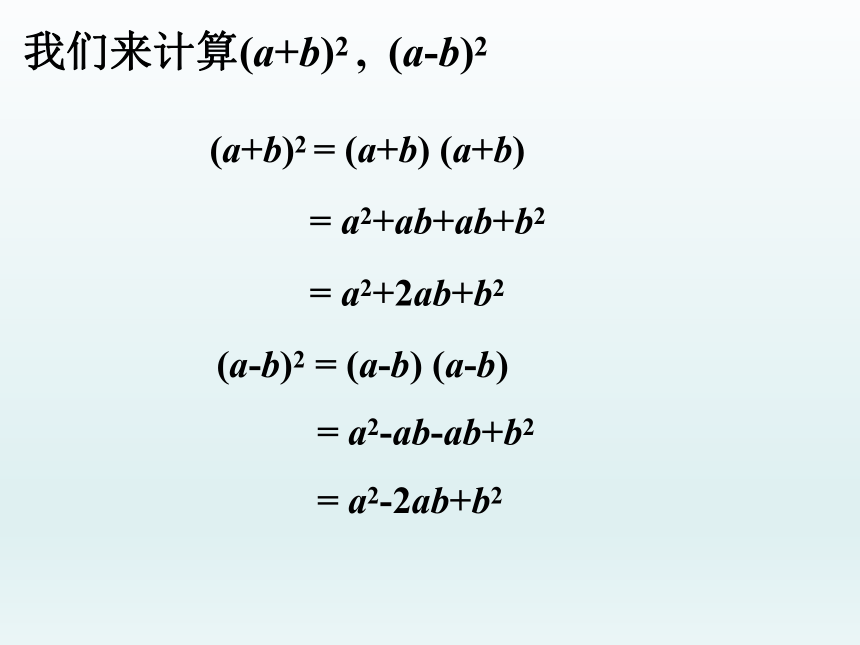





文档简介
课件20张PPT。14.2.2 完全平方公式第十四章 整式的乘法与因式分解探究
计算下列各式,你能发现什么规律?
(p+1)2 = (p+1) (p+1) = ______
(m+2)2= _________;
(p-1)2 = (p-1 ) (p-1) = ________;
(m-2)2 = __________.p2+2p+1m2+4m+4p2-2p+1m2-4m+4我们来计算(a+b)2 , (a-b)2(a+b)2 = (a+b) (a+b)(a-b)2 = (a-b) (a-b)= a2+ab+ab+b2= a2+2ab+b2= a2-ab-ab+b2= a2-2ab+b2即两数和(或差)的平方,等于它们的
平方和,加(或减)它们的积的2倍. (a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab +b2这两个公式叫做(乘法的)完全平方公式首平方,尾平方
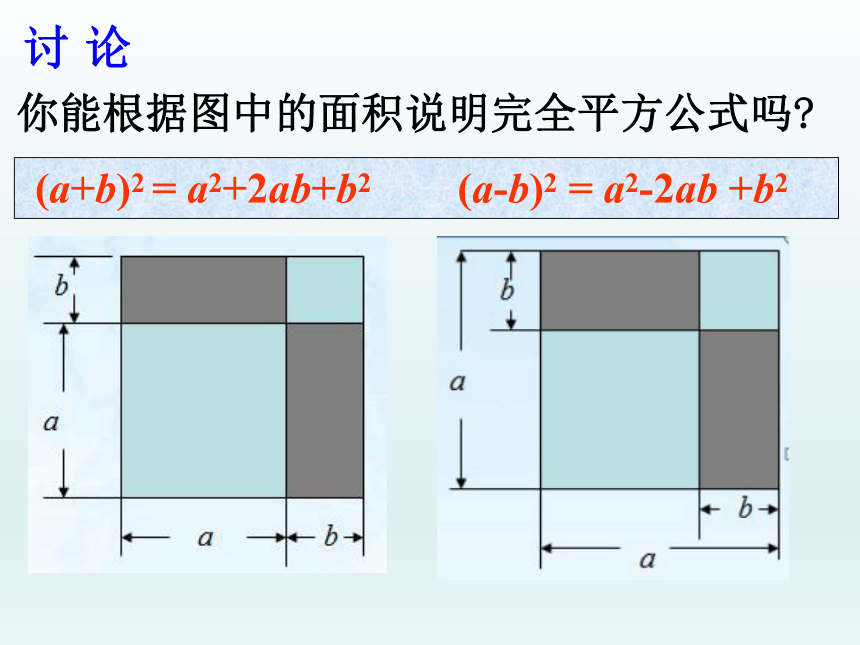
积的2倍在中央你能根据图中的面积说明完全平方公式吗?讨 论 (a+b)2 = a2+2ab+b2 (a-b)2 = a2-2ab +b2例、运用完全平方公式计算:
(1) (4m+n)2 (2) (y - )2解: (1) (4m+n) 2 = (4m)2 + 2?(4m)?n+n2
= 16m2+8mn +n2(5) (3a+b)2 (6) (-3+2a)2
(7) (x-2y)2 (8) (-2x-3y)2例、运用完全平方公式计算:
(1) 1022 (2) 992 解: (1) 1022 = (100 +2) 2
= 1002 +2×100 × 2 + 22
= 10 000 +400 +4
= 10 404 (2) 992 = (100 -1)2
= 1002 -2 × 100 × 1+12
= 10 000 - 200 + 1
= 9 801思考
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
如何计算(x+y+z)2 ? 填空:
1) a2+ +b2=(a+b)2
2) a2+ +b2=(a - b)2
3) 4a2+ +b2=(2a+b)2
4) 4a2+ +b2=(2a - b)2
5) ( )2+4ab+b2=( +b)2
6) a2-8ab+ =( )22ab(-2ab)4ab(-4ab)2a2a16b2a-4b拓展提升1、计算(2a+3b)2-2(2a+3b)(a+2b)+(a+2b)2 .2、已知x+y=4,xy= -13,求x2-3xy+y2的值.拓展提升2、证明:无论a,b为何值,多项式
a2+b2-2a-6b+12的值恒为正.3、已知ΔABC的三边长a,b,c,满足
a2+b2+c2-ab-bc-ac=0,试判断
ΔABC的形状. 添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号。a+(b+c) = a+b+c
a- (b+c) = a - b – ca + b + c = a + ( b + c)
a – b – c = a – ( b + c ) 练 习
1、在等号右边的括号内填上适当的项:
(1) a + b + c = a + ( )
(2) a – b – c = a – ( )
(3) a - b + c = a – ( )
(4) a + b + c = a - ( )b + c b + c b - c - b - c 例、运用乘法公式计算:
( x +2y-3) (x- 2y +3) (2) (a + b +c ) 2解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9 (a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac例、运用乘法公式计算:
( x +2y-3) (x- 2y +3) (2) (a + b +c ) 22、运用乘法公式计算:
(1) (a + 2b – 1 ) 2
(2) (2x +y +z ) (2x – y – z )3、如图,一块直径为a+b的圆形钢板, 从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.
计算下列各式,你能发现什么规律?
(p+1)2 = (p+1) (p+1) = ______
(m+2)2= _________;
(p-1)2 = (p-1 ) (p-1) = ________;
(m-2)2 = __________.p2+2p+1m2+4m+4p2-2p+1m2-4m+4我们来计算(a+b)2 , (a-b)2(a+b)2 = (a+b) (a+b)(a-b)2 = (a-b) (a-b)= a2+ab+ab+b2= a2+2ab+b2= a2-ab-ab+b2= a2-2ab+b2即两数和(或差)的平方,等于它们的
平方和,加(或减)它们的积的2倍. (a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab +b2这两个公式叫做(乘法的)完全平方公式首平方,尾平方
积的2倍在中央你能根据图中的面积说明完全平方公式吗?讨 论 (a+b)2 = a2+2ab+b2 (a-b)2 = a2-2ab +b2例、运用完全平方公式计算:
(1) (4m+n)2 (2) (y - )2解: (1) (4m+n) 2 = (4m)2 + 2?(4m)?n+n2
= 16m2+8mn +n2(5) (3a+b)2 (6) (-3+2a)2
(7) (x-2y)2 (8) (-2x-3y)2例、运用完全平方公式计算:
(1) 1022 (2) 992 解: (1) 1022 = (100 +2) 2
= 1002 +2×100 × 2 + 22
= 10 000 +400 +4
= 10 404 (2) 992 = (100 -1)2
= 1002 -2 × 100 × 1+12
= 10 000 - 200 + 1
= 9 801思考
(a+b)2与(-a-b)2相等吗?
(a-b)2与(b-a)2相等吗?
如何计算(x+y+z)2 ? 填空:
1) a2+ +b2=(a+b)2
2) a2+ +b2=(a - b)2
3) 4a2+ +b2=(2a+b)2
4) 4a2+ +b2=(2a - b)2
5) ( )2+4ab+b2=( +b)2
6) a2-8ab+ =( )22ab(-2ab)4ab(-4ab)2a2a16b2a-4b拓展提升1、计算(2a+3b)2-2(2a+3b)(a+2b)+(a+2b)2 .2、已知x+y=4,xy= -13,求x2-3xy+y2的值.拓展提升2、证明:无论a,b为何值,多项式
a2+b2-2a-6b+12的值恒为正.3、已知ΔABC的三边长a,b,c,满足
a2+b2+c2-ab-bc-ac=0,试判断
ΔABC的形状. 添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号。a+(b+c) = a+b+c
a- (b+c) = a - b – ca + b + c = a + ( b + c)
a – b – c = a – ( b + c ) 练 习
1、在等号右边的括号内填上适当的项:
(1) a + b + c = a + ( )
(2) a – b – c = a – ( )
(3) a - b + c = a – ( )
(4) a + b + c = a - ( )b + c b + c b - c - b - c 例、运用乘法公式计算:
( x +2y-3) (x- 2y +3) (2) (a + b +c ) 2解: (1) ( x +2y-3) (x- 2y +3)
= [ x+ (2y – 3 )] [ x- (2y-3) ]
= x2- (2y- 3)2
= x2- ( 4y2-12y+9)
= x2-4y2+12y-9 (a + b +c ) 2
= [ (a+b) +c ]2
= (a+b)2 +2 (a+b)c +c2
= a2+2ab +b2 +2ac +2bc +c2
= a2+b2+c2 +2ab+2bc +2ac例、运用乘法公式计算:
( x +2y-3) (x- 2y +3) (2) (a + b +c ) 22、运用乘法公式计算:
(1) (a + 2b – 1 ) 2
(2) (2x +y +z ) (2x – y – z )3、如图,一块直径为a+b的圆形钢板, 从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.
