一年级上册数学单元测试-3.分一分、认识图形 西师大版(含答案)
文档属性
| 名称 | 一年级上册数学单元测试-3.分一分、认识图形 西师大版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 99.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-19 00:00:00 | ||
图片预览

文档简介
一年级上册数学单元测试-3.分一分、认识图形
一、单选题
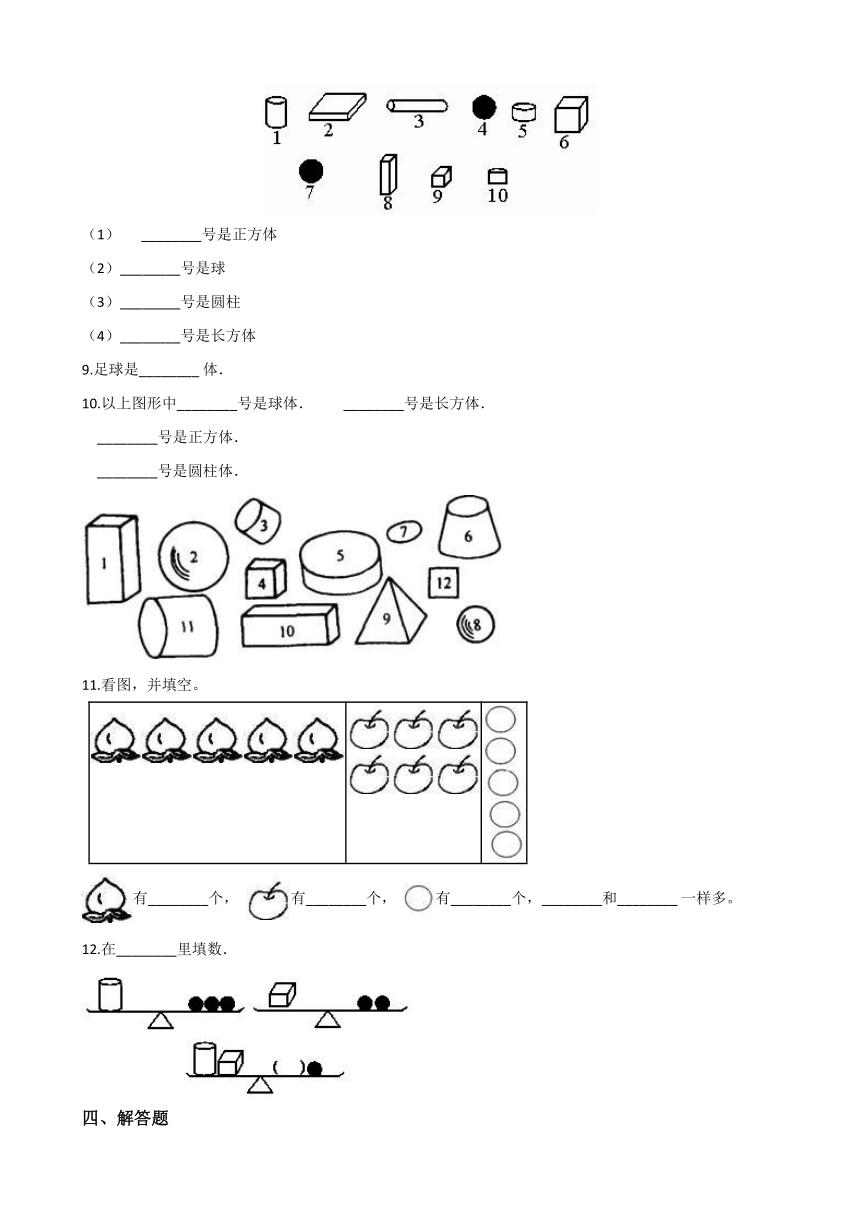
1.下图中,有________个球。 (? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
2.下面图形,最容易稳定立住的图形是(?? )。
A.???????????????????????????????????B.???????????????????????????????????C.?
3.如图所示为某几何体的展开图,那么这个几何体的棱的条数为(?? )
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?7
4.一个正方体的棱长总和是60厘米,它的表面积是(???? )。
A.?21600平方厘米??????????????????????????B.?150平方厘米??????????????????????????C.?125立方厘米
二、判断题
5.判断正误. 这是一个球体。(? )
6.长方体就是正方体。( ?? )
7.一张复印纸是长方体.( ??)
三、填空题
8.(按题中序号的顺序填写)
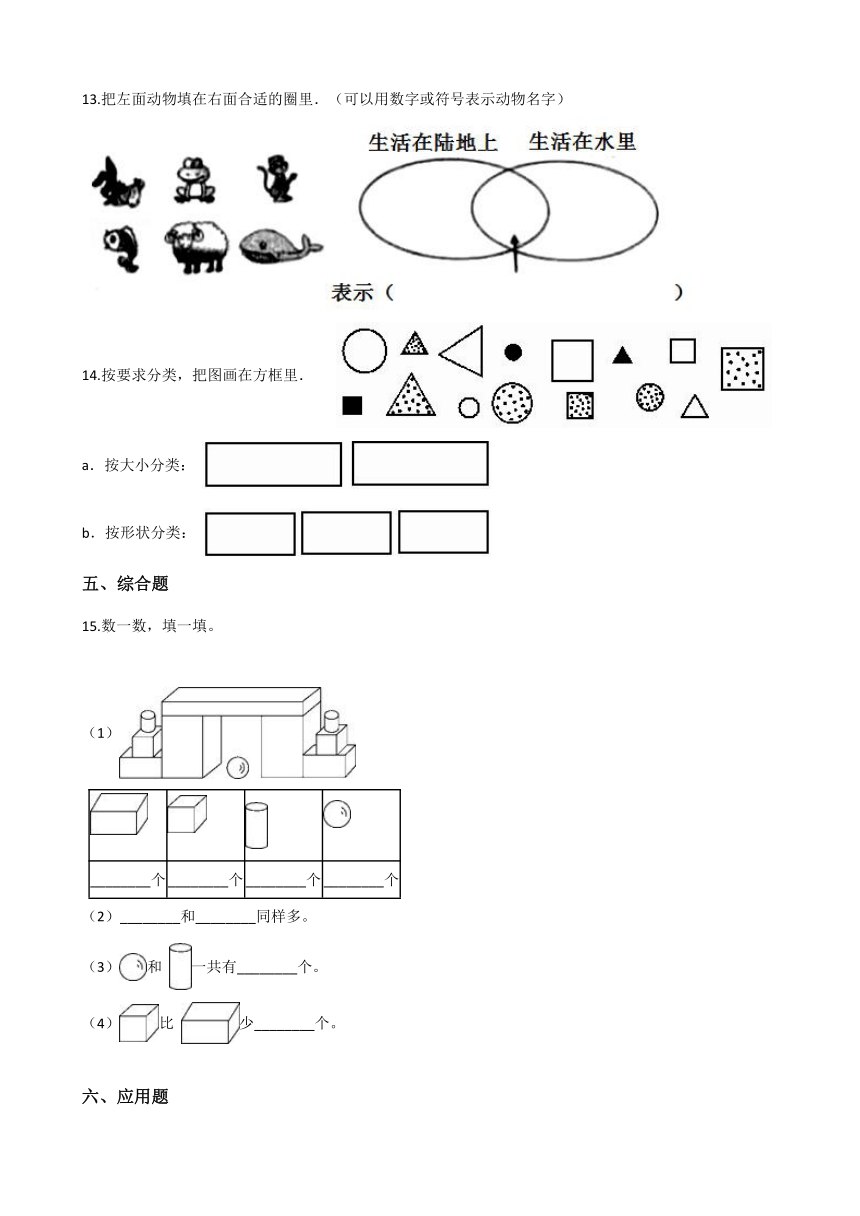
(1)???? ________号是正方体
(2)________号是球
(3)________号是圆柱
(4)________号是长方体
9.足球是________?体.
10.以上图形中________号是球体. ________号是长方体. ________号是正方体. ________号是圆柱体.
11.看图,并填空。
有________个, 有________个, 有________个,________和________?一样多。
12.在________里填数.
四、解答题
13.把左面动物填在右面合适的圈里.(可以用数字或符号表示动物名字)
14.按要求分类,把图画在方框里. a.按大小分类: b.按形状分类:
五、综合题
15.数一数,填一填。?
(1)
________个
________个
________个
________个
(2)________和________同样多。
(3)和 一共有________个。
(4)比 少________个。
六、应用题
16.一个长方体的长和宽相等,都是4厘米。如果将高去掉2厘米,这个长方体就成为一个正方体,原来长方体的表面积是多少平方厘米?
参考答案
一、单选题
1.【答案】B
【解析】
2.【答案】B
【解析】【解答】图形B是由长方体和圆柱体组成的,最容易稳定立柱.故选:B.
【分析】这道题主要考查了学生对立体图形的特征的掌握情况.解答此题的关键是根据立体图形的基本特征进行判断.
3.【答案】 B
【解析】【解答】解:这个几何体左右两个面是三角形,另外三个面是长方形,两个三角形有6条棱,只剩下3个长方形的3条棱,共6+3=9(条) 故答案为:B
【分析】这个几何体左右两个三角形的边与长方形的宽是重合的,三个长方形的长也是重合的,一定要去掉重合的棱的条数.
4.【答案】 B
【解析】【解答】60÷12=5(厘米)
5×5×6=150(平方厘米)
【分析】正方体总共有12条棱,长度全都相等,所以知道了总棱长是60厘米,就可以求出其中一条棱长是5厘米,再带入公式“正方体的表面积=棱长×棱长×6”求出它的表面积是150平方厘米。
二、判断题
5.【答案】错误
【解析】
6.【答案】错误
【解析】
7.【答案】正确
【解析】
三、填空题
8.【答案】(1)6
(2)4,7
(3)1,3,5
(4)2,8,9
【解析】
9.【答案】球体
【解析】
10.【答案】2,8;1,10;4;3、5,11
【解析】
11.【答案】5;6 ;5 ;;
【解析】
12.【答案】4
【解析】
四、解答题
13.【答案】
【解析】【分析】明确两个椭圆相交的公共部分表示:这部分动物既可以在陆地上生活,也可以在水中生活。
14.【答案】
【解析】
五、综合题
15.【答案】(1)5;2;2;1 (2)正方体;圆柱 (3)3 (4)3
【解析】
六、应用题
16.【答案】解:4+2=6(厘米) 长方形面积=(4×6+4×6+4×4)×2=128(平方厘米) 答:原来长方体的表面积是128平方厘米。
【解析】【分析】高去掉2厘米后,这个长方体就成为一个正方体,高去掉2厘米后,就变成了4厘米,求出原来的高是6厘米,带入公式“长方体的表面积=(长×宽+长×高+宽×高)×2”算出总面积。
一、单选题
1.下图中,有________个球。 (? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
2.下面图形,最容易稳定立住的图形是(?? )。
A.???????????????????????????????????B.???????????????????????????????????C.?
3.如图所示为某几何体的展开图,那么这个几何体的棱的条数为(?? )
A.?10???????????????????????????????????????????B.?9???????????????????????????????????????????C.?8???????????????????????????????????????????D.?7
4.一个正方体的棱长总和是60厘米,它的表面积是(???? )。
A.?21600平方厘米??????????????????????????B.?150平方厘米??????????????????????????C.?125立方厘米
二、判断题
5.判断正误. 这是一个球体。(? )
6.长方体就是正方体。( ?? )
7.一张复印纸是长方体.( ??)
三、填空题
8.(按题中序号的顺序填写)
(1)???? ________号是正方体
(2)________号是球
(3)________号是圆柱
(4)________号是长方体
9.足球是________?体.
10.以上图形中________号是球体. ________号是长方体. ________号是正方体. ________号是圆柱体.
11.看图,并填空。
有________个, 有________个, 有________个,________和________?一样多。
12.在________里填数.
四、解答题
13.把左面动物填在右面合适的圈里.(可以用数字或符号表示动物名字)
14.按要求分类,把图画在方框里. a.按大小分类: b.按形状分类:
五、综合题
15.数一数,填一填。?
(1)
________个
________个
________个
________个
(2)________和________同样多。
(3)和 一共有________个。
(4)比 少________个。
六、应用题
16.一个长方体的长和宽相等,都是4厘米。如果将高去掉2厘米,这个长方体就成为一个正方体,原来长方体的表面积是多少平方厘米?
参考答案
一、单选题
1.【答案】B
【解析】
2.【答案】B
【解析】【解答】图形B是由长方体和圆柱体组成的,最容易稳定立柱.故选:B.
【分析】这道题主要考查了学生对立体图形的特征的掌握情况.解答此题的关键是根据立体图形的基本特征进行判断.
3.【答案】 B
【解析】【解答】解:这个几何体左右两个面是三角形,另外三个面是长方形,两个三角形有6条棱,只剩下3个长方形的3条棱,共6+3=9(条) 故答案为:B
【分析】这个几何体左右两个三角形的边与长方形的宽是重合的,三个长方形的长也是重合的,一定要去掉重合的棱的条数.
4.【答案】 B
【解析】【解答】60÷12=5(厘米)
5×5×6=150(平方厘米)
【分析】正方体总共有12条棱,长度全都相等,所以知道了总棱长是60厘米,就可以求出其中一条棱长是5厘米,再带入公式“正方体的表面积=棱长×棱长×6”求出它的表面积是150平方厘米。
二、判断题
5.【答案】错误
【解析】
6.【答案】错误
【解析】
7.【答案】正确
【解析】
三、填空题
8.【答案】(1)6
(2)4,7
(3)1,3,5
(4)2,8,9
【解析】
9.【答案】球体
【解析】
10.【答案】2,8;1,10;4;3、5,11
【解析】
11.【答案】5;6 ;5 ;;
【解析】
12.【答案】4
【解析】
四、解答题
13.【答案】
【解析】【分析】明确两个椭圆相交的公共部分表示:这部分动物既可以在陆地上生活,也可以在水中生活。
14.【答案】
【解析】
五、综合题
15.【答案】(1)5;2;2;1 (2)正方体;圆柱 (3)3 (4)3
【解析】
六、应用题
16.【答案】解:4+2=6(厘米) 长方形面积=(4×6+4×6+4×4)×2=128(平方厘米) 答:原来长方体的表面积是128平方厘米。
【解析】【分析】高去掉2厘米后,这个长方体就成为一个正方体,高去掉2厘米后,就变成了4厘米,求出原来的高是6厘米,带入公式“长方体的表面积=(长×宽+长×高+宽×高)×2”算出总面积。
