高中数学北师大版必修五课件 第二章 解三角形习题课2 :34张PPT
文档属性
| 名称 | 高中数学北师大版必修五课件 第二章 解三角形习题课2 :34张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 914.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览








文档简介
课件34张PPT。习题课 正弦定理、余弦定理的综合应用一、常用术语
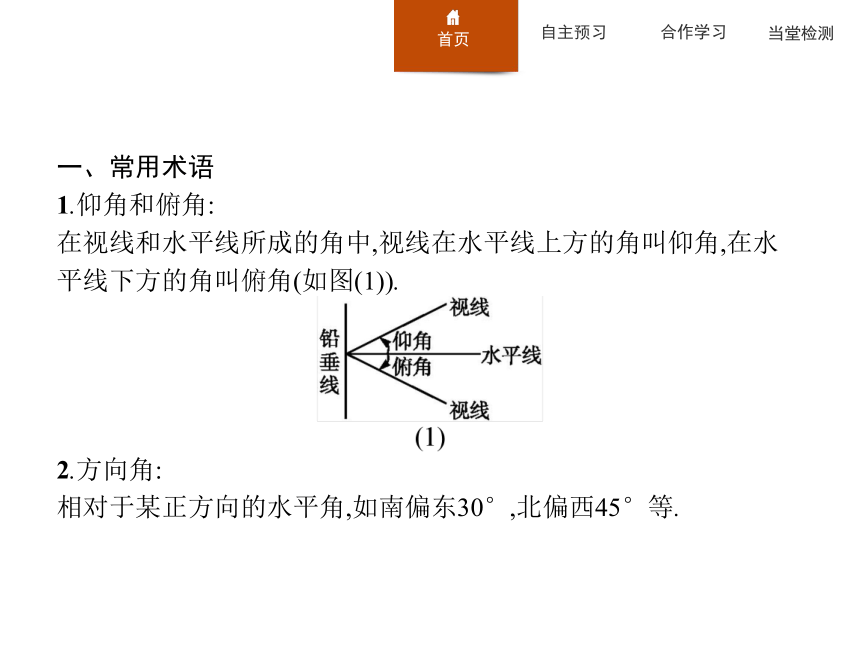
1.仰角和俯角:
在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图(1)).
2.方向角:
相对于某正方向的水平角,如南偏东30°,北偏西45°等.3.方位角:
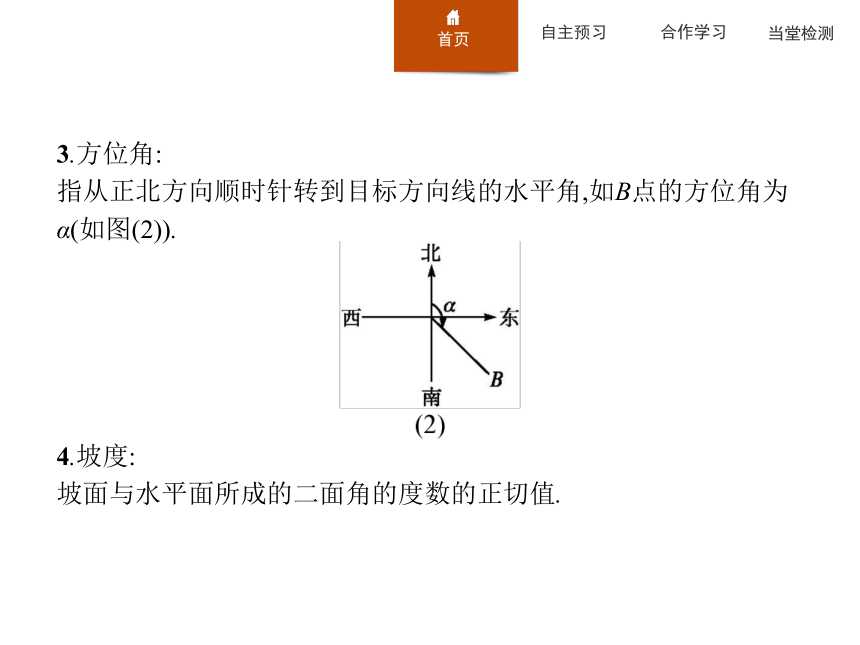
指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图(2)).
4.坡度:
坡面与水平面所成的二面角的度数的正切值.二、正弦、余弦定理和面积公式
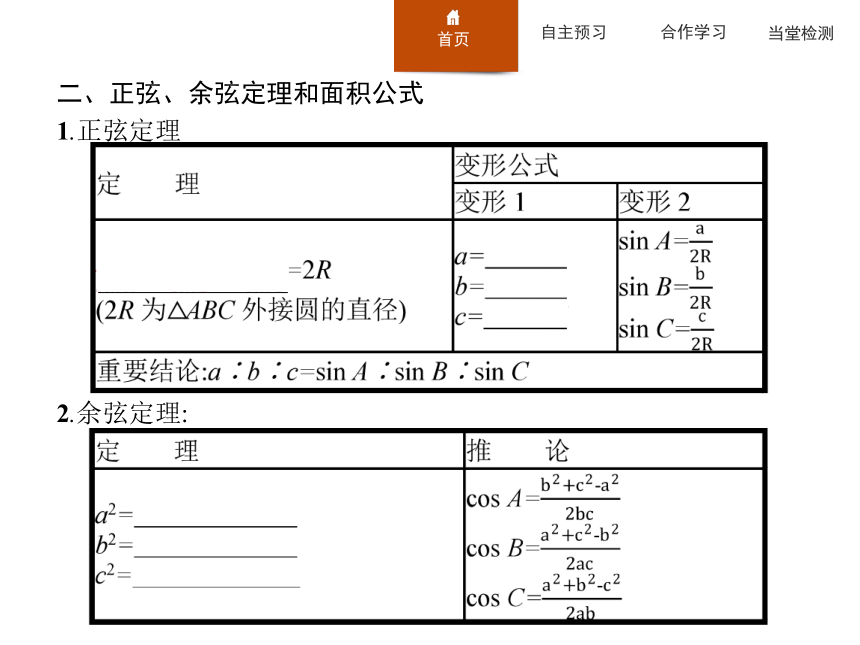
1.正弦定理2.余弦定理: 答案:B 解析:由B=2A,得sin B=sin 2A, 答案:B 【做一做3】(2016天津高考)在△ABC中,若 ,BC=3,
∠C=120°,则AC=( )?
A.1 B.2
C.3 D.4
解析:由余弦定理得13=9+AC2+3AC?AC=1.
故选A.
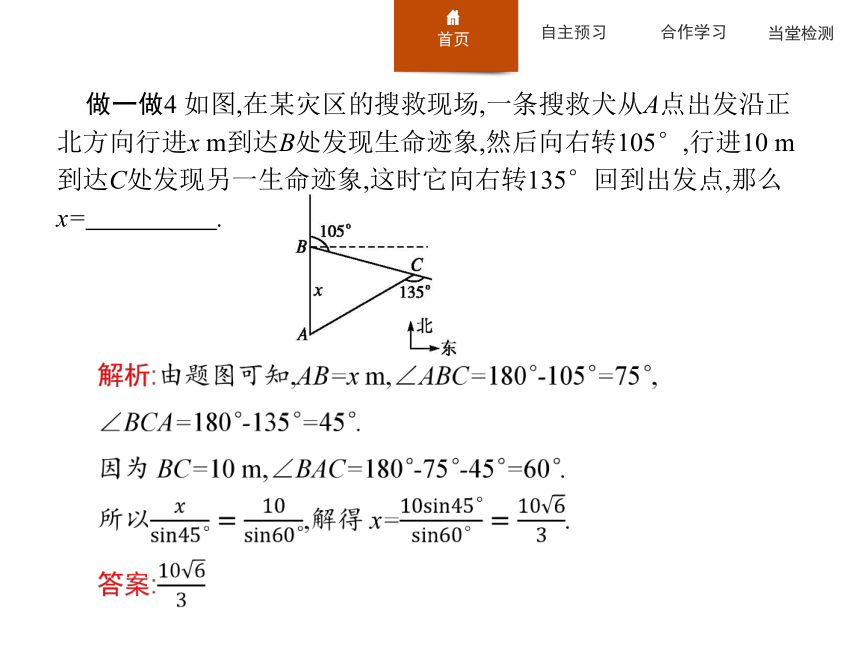
答案:A做一做4?如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10 m到达C处发现另一生命迹象,这时它向右转135°回到出发点,那么x= .?探究一探究二探究三规范解答
【例1】 在△ABC中,a,b,c分别表示三个内角A,B,C的对边,若(a2+b2)sin (A-B)=(a2-b2)sin (A+B),则△ABC的形状为( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
解析:由已知(a2+b2)sin(A-B)=(a2-b2)·sin(A+B).
得a2[sin(A-B)-sin(A+B)]=b2[-sin(A+B)-sin(A-B)],
所以2a2cos Asin B=2b2cos Bsin A.
由正弦定理得sin2Acos Asin B=sin2Bcos Bsin A.
即sin 2Asin Asin B=sin 2Bsin Asin B.
因为0所以2A=2B或2A=π-2B.所以△ABC是等腰三角形或直角三角形.
答案:D探究一探究二探究三规范解答反思感悟1.确定三角形的形状主要途径有两个:一是化边为角,二是化角为边;
2.实现方法可以通过正弦定理、余弦定理实现边角转换,也可以通过三角变换找出角之间的关系,还可以利用代数式的化简或变形找出边之间的关系.探究一探究二探究三规范解答 变式训练1 已知在△ABC中, (a,b,c分别为角A,B,C的对边),则△ABC的形状为( )?
A.等边三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
答案:B探究一探究二探究三规范解答
【例2】 在△ABC中,内角A,B,C的对边分别为a,b,c.探究一探究二探究三规范解答探究一探究二探究三规范解答反思感悟 探究一探究二探究三规范解答变式训练2 ?(1)求sin ∠CED的值;
(2)求BE的长.探究一探究二探究三规范解答解:设∠CED=α.
(1)在△CDE中,由余弦定理,
得EC2=CD2+DE2-2CD·DE·cos ∠EDC.
于是由题设知,7=CD2+1+CD,即CD2+CD-6=0,
解得CD=2(CD=-3舍去).探究一探究二探究三规范解答探究一探究二探究三规范解答【例3】从A处下山到C处有两种途径,一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行.速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min.山路AC长为1 260 m,经测量,
(1)求索道AB的长.
(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?探究一探究二探究三规范解答分析:(1)先利用三角变换公式,求出sin B,再利用正弦定理求出AB的长;
(2)先利用余弦定理,列出关于时间t的关系式,再利用函数性质求其最值.探究一探究二探究三规范解答探究一探究二探究三规范解答反思感悟(1)三角形应用题主要是解决三类问题:测高度、测距离和测角度.
(2)在解三角形时,要根据具体的已知条件合理选择解法,同时,不可将正弦定理与余弦定理割裂开来,有时需综合运用.
(3)在解决与三角形有关的实际问题时,首先要明确题意,正确画出平面图形或空间图形,然后根据条件和图形特点将问题归纳到三角形中解决.要明确先用哪个公式或定理,先求哪些量,确定解三角形的方法.在演算过程中,要算法简练、算式工整、计算正确,还要注意近似计算的要求.
(4)在画图和识图过程中要准确理解题目中所涉及的几种角,如仰角、俯角、方位角,以防出错.探究一探究二探究三规范解答变式训练3 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时,小艇与轮船相遇.假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.?探究一探究二探究三规范解答探究一探究二探究三规范解答解三角形知识在实际问题中的应用
【典例】某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC,△ABD,经测量AD=BD=14,BC=10,AC=16,C=D.
(1)求边AB的长度.
(2)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用较低,请说明理由.
分析:(1)在△ABC和△ABD中,根据余弦定理列出方程组求解;(2)利用三角形面积公式比较大小.探究一探究二探究三规范解答规范解答 (1)在△ABC中,由余弦定理得
AB2=AC2+BC2-2AC·BCcos C
=162+102-2×16×10cos C.
在△ABD中,由余弦定理及C=D,
整理得AB2=AD2+BD2-2AD·BDcos D
=142+142-2×142cos C,
得142+142-2×142cos C=162+102-2×16×10cos C,又C为三角形的内角,所以C=60°,
又C=D,AD=BD,所以△ABD是等边三角形,
即边AB的长度为14.探究一探究二探究三规范解答(2)小李的设计符合要求.理由如下:
?
因为AD·BD>AC·BC,所以S△ABD>S△ABC,
由已知建造费用与用地面积成正比,故选择△ABC建造环境标志费用较低.
即小李的设计使建造费用较低.探究一探究二探究三规范解答反思提升1.本题是典型的解三角形知识在实际中的应用问题,同时也是一道小型的建模问题,解题的关键是抽象出模型.
2.解决本题要关注两个点:一是充分利用C=D这一条件,二是抽象出的三角模型还要回归到实际问题中,以便做出合理的选择.12345答案:D 12345答案:B 123453.一艘海轮从A处出发,以每小时40 n mile的速度沿东偏南50°方向直线航行,30 min后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,则B,C两点间的距离是( )答案:A 123454.在△ABC中,a,b,c分别为角A,B,C的对边,已知a,b,c成等比数列,且a2-c2=ac-bc,则A= ,△ABC的形状为 .?
解析:因为a,b,c成等比数列,所以b2=ac.
又a2-c2=ac-bc,所以b2+c2-a2=bc.
在△ABC中,整理得(b-c)(b3+c3+cb2)=0,
所以b=c,所以△ABC为正三角形.
答案:60° 正三角形1234512345
1.仰角和俯角:
在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图(1)).
2.方向角:
相对于某正方向的水平角,如南偏东30°,北偏西45°等.3.方位角:
指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图(2)).
4.坡度:
坡面与水平面所成的二面角的度数的正切值.二、正弦、余弦定理和面积公式
1.正弦定理2.余弦定理: 答案:B 解析:由B=2A,得sin B=sin 2A, 答案:B 【做一做3】(2016天津高考)在△ABC中,若 ,BC=3,
∠C=120°,则AC=( )?
A.1 B.2
C.3 D.4
解析:由余弦定理得13=9+AC2+3AC?AC=1.
故选A.
答案:A做一做4?如图,在某灾区的搜救现场,一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象,然后向右转105°,行进10 m到达C处发现另一生命迹象,这时它向右转135°回到出发点,那么x= .?探究一探究二探究三规范解答
【例1】 在△ABC中,a,b,c分别表示三个内角A,B,C的对边,若(a2+b2)sin (A-B)=(a2-b2)sin (A+B),则△ABC的形状为( )
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形或直角三角形
解析:由已知(a2+b2)sin(A-B)=(a2-b2)·sin(A+B).
得a2[sin(A-B)-sin(A+B)]=b2[-sin(A+B)-sin(A-B)],
所以2a2cos Asin B=2b2cos Bsin A.
由正弦定理得sin2Acos Asin B=sin2Bcos Bsin A.
即sin 2Asin Asin B=sin 2Bsin Asin B.
因为0
答案:D探究一探究二探究三规范解答反思感悟1.确定三角形的形状主要途径有两个:一是化边为角,二是化角为边;
2.实现方法可以通过正弦定理、余弦定理实现边角转换,也可以通过三角变换找出角之间的关系,还可以利用代数式的化简或变形找出边之间的关系.探究一探究二探究三规范解答 变式训练1 已知在△ABC中, (a,b,c分别为角A,B,C的对边),则△ABC的形状为( )?
A.等边三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
答案:B探究一探究二探究三规范解答
【例2】 在△ABC中,内角A,B,C的对边分别为a,b,c.探究一探究二探究三规范解答探究一探究二探究三规范解答反思感悟 探究一探究二探究三规范解答变式训练2 ?(1)求sin ∠CED的值;
(2)求BE的长.探究一探究二探究三规范解答解:设∠CED=α.
(1)在△CDE中,由余弦定理,
得EC2=CD2+DE2-2CD·DE·cos ∠EDC.
于是由题设知,7=CD2+1+CD,即CD2+CD-6=0,
解得CD=2(CD=-3舍去).探究一探究二探究三规范解答探究一探究二探究三规范解答【例3】从A处下山到C处有两种途径,一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行.速度为50 m/min.在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130 m/min.山路AC长为1 260 m,经测量,
(1)求索道AB的长.
(2)问:乙出发多少分钟后,乙在缆车上与甲的距离最短?探究一探究二探究三规范解答分析:(1)先利用三角变换公式,求出sin B,再利用正弦定理求出AB的长;
(2)先利用余弦定理,列出关于时间t的关系式,再利用函数性质求其最值.探究一探究二探究三规范解答探究一探究二探究三规范解答反思感悟(1)三角形应用题主要是解决三类问题:测高度、测距离和测角度.
(2)在解三角形时,要根据具体的已知条件合理选择解法,同时,不可将正弦定理与余弦定理割裂开来,有时需综合运用.
(3)在解决与三角形有关的实际问题时,首先要明确题意,正确画出平面图形或空间图形,然后根据条件和图形特点将问题归纳到三角形中解决.要明确先用哪个公式或定理,先求哪些量,确定解三角形的方法.在演算过程中,要算法简练、算式工整、计算正确,还要注意近似计算的要求.
(4)在画图和识图过程中要准确理解题目中所涉及的几种角,如仰角、俯角、方位角,以防出错.探究一探究二探究三规范解答变式训练3 某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,经过t小时,小艇与轮船相遇.假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.?探究一探究二探究三规范解答探究一探究二探究三规范解答解三角形知识在实际问题中的应用
【典例】某城市有一块不规则的绿地如图所示,城建部门欲在该地上建造一个底座为三角形的环境标志,小李、小王设计的底座形状分别为△ABC,△ABD,经测量AD=BD=14,BC=10,AC=16,C=D.
(1)求边AB的长度.
(2)若建造环境标志的费用与用地面积成正比,不考虑其他因素,小李、小王谁的设计使建造费用较低,请说明理由.
分析:(1)在△ABC和△ABD中,根据余弦定理列出方程组求解;(2)利用三角形面积公式比较大小.探究一探究二探究三规范解答规范解答 (1)在△ABC中,由余弦定理得
AB2=AC2+BC2-2AC·BCcos C
=162+102-2×16×10cos C.
在△ABD中,由余弦定理及C=D,
整理得AB2=AD2+BD2-2AD·BDcos D
=142+142-2×142cos C,
得142+142-2×142cos C=162+102-2×16×10cos C,又C为三角形的内角,所以C=60°,
又C=D,AD=BD,所以△ABD是等边三角形,
即边AB的长度为14.探究一探究二探究三规范解答(2)小李的设计符合要求.理由如下:
?
因为AD·BD>AC·BC,所以S△ABD>S△ABC,
由已知建造费用与用地面积成正比,故选择△ABC建造环境标志费用较低.
即小李的设计使建造费用较低.探究一探究二探究三规范解答反思提升1.本题是典型的解三角形知识在实际中的应用问题,同时也是一道小型的建模问题,解题的关键是抽象出模型.
2.解决本题要关注两个点:一是充分利用C=D这一条件,二是抽象出的三角模型还要回归到实际问题中,以便做出合理的选择.12345答案:D 12345答案:B 123453.一艘海轮从A处出发,以每小时40 n mile的速度沿东偏南50°方向直线航行,30 min后到达B处,在C处有一座灯塔,海轮在A处观察灯塔,其方向是东偏南20°,在B处观察灯塔,其方向是北偏东65°,则B,C两点间的距离是( )答案:A 123454.在△ABC中,a,b,c分别为角A,B,C的对边,已知a,b,c成等比数列,且a2-c2=ac-bc,则A= ,△ABC的形状为 .?
解析:因为a,b,c成等比数列,所以b2=ac.
又a2-c2=ac-bc,所以b2+c2-a2=bc.
在△ABC中,整理得(b-c)(b3+c3+cb2)=0,
所以b=c,所以△ABC为正三角形.
答案:60° 正三角形1234512345
