5.1.1 相交线课件
图片预览





文档简介
(共18张PPT)
情景引入
1.这一组图片有什么共同特点?
情景引入
2.如图,观察剪刀剪开布片的过程中有关角的变化是怎样呢?
探究新知
如图,把两根木条用钉子钉在一起,转动其中一根木条,观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗?
探究新知
1
2
3
4
A
B
C
D
形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
图中还有哪些角也是邻补角呢?
∠2 和∠3
∠3 和∠4
∠4 和∠1
探究新知
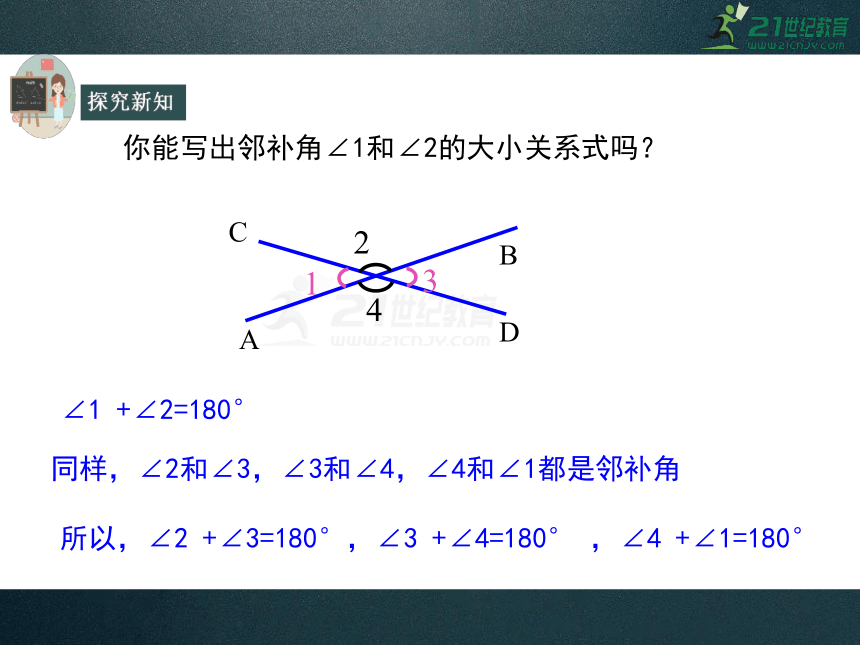
你能写出邻补角∠1和∠2的大小关系式吗?
∠1 +∠2=180°
同样,∠2和∠3,∠3和∠4,∠4和∠1都是邻补角
所以,∠2 +∠3=180°,∠3 +∠4=180° ,∠4 +∠1=180°
探究新知
1
2
3
4
A
B
C
D
O
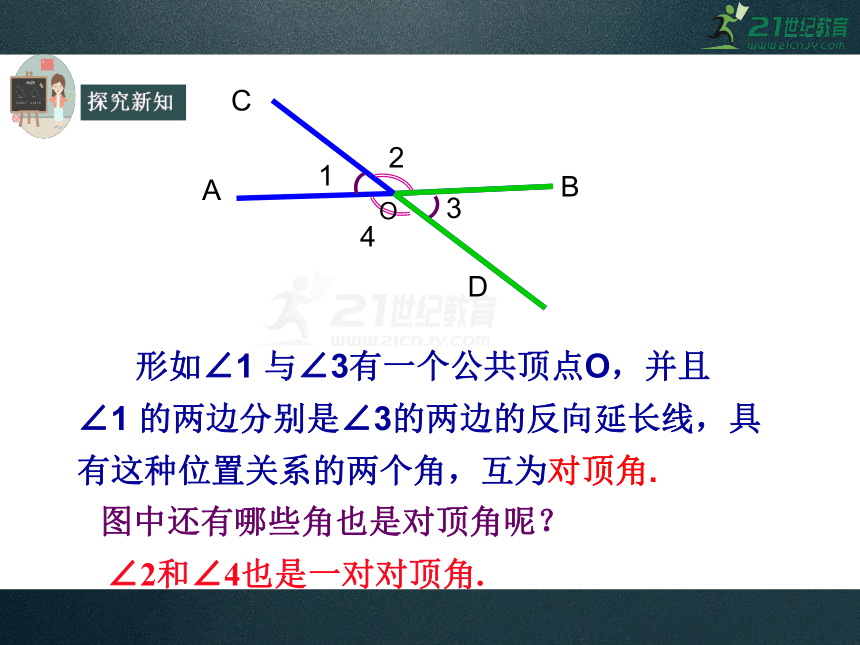
图中还有哪些角也是对顶角呢?
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
∠2和∠4也是一对对顶角.
探究新知
1
2
1
2
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
判断下列各图中∠1和∠2是否为对顶角,并说明理由?
√
探究新知
∠ 2 +∠3= ,
你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3
180°
180°
由同角的补角相等可知
动动脑:为什么?
因此可得对顶角的性质:对顶角相等
探究新知
如图,直线AB、CD相交于-点O,
若∠1=28°,则∠2=_____.
28°
例题讲解
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
a
b
)
(
1
4
2
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
)
3
课堂练习
一、判断题(在正确的后面打“ ” ,在错误的后面打“ ”。)
(1)对顶角相等。 ( )
√
√
(2)相等的角是对顶角。 ( )
(3)有公共顶点且相等的两个角是对顶角。 ( )
(4)不相邻的两个角一定不是对顶角。 ( )
√
X
X
X
随堂练习
1.如图,直线AB与CD相交于点O,直线OE垂直直线CD,若∠ BOE=30°,则AOD的度数为( )
C
E
O
D
B
A
A.120 ° B.130 ° C.150 ° D.160 °
A
随堂练习
2.如图,直线AB与CD相交于点O,已知∠ AOD=165°,则∠ BOC的大小为( )
C
O
D
B
A
A.120 ° B.130 ° C.150 ° D.165 °
D
随堂练习
3.下面四个图形中,∠ 1与∠ 2是对顶角的为( )
C
1
2
1
2
1
2
1
2
A.
C.
B.
D.
拓展延伸
如图,直线AB、CD相交于点O,OA平分∠ EOC, ∠ EOC=60°,则∠ BOD的度数是多少度?
C
O
D
B
A
E
解:∵ OA平分∠ EOC, ∠ EOC=60°。 ∴ ∠ AOC=30°, (角平分线定义)
∴ ∠ BOD= ∠ AOC=60°(对顶角相等)
课堂小结
1.对顶角的概念:
一个角的两边是另一个角两边的反向延长线,具有这种位置 关系的两个角叫做对顶角。
2.互为邻补角的定义:
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
3.不重合的两条直线相交形成四个角邻补角的性质:
有四对邻补角,两对对顶角。
https://www.21cnjy.com/help/help_extract.php
情景引入
1.这一组图片有什么共同特点?
情景引入
2.如图,观察剪刀剪开布片的过程中有关角的变化是怎样呢?
探究新知
如图,把两根木条用钉子钉在一起,转动其中一根木条,观察两根木条所形成的角的位置及大小关系.
你能动手画出两条相交直线吗?
探究新知
1
2
3
4
A
B
C
D
形如∠1 与∠2有一条公共边OC,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角.
O
图中还有哪些角也是邻补角呢?
∠2 和∠3
∠3 和∠4
∠4 和∠1
探究新知
你能写出邻补角∠1和∠2的大小关系式吗?
∠1 +∠2=180°
同样,∠2和∠3,∠3和∠4,∠4和∠1都是邻补角
所以,∠2 +∠3=180°,∠3 +∠4=180° ,∠4 +∠1=180°
探究新知
1
2
3
4
A
B
C
D
O
图中还有哪些角也是对顶角呢?
形如∠1 与∠3有一个公共顶点O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
∠2和∠4也是一对对顶角.
探究新知
1
2
1
2
1
2
1
2
1
2
1
2
(1)
(2)
(3)
(4)
(5)
(6)
判断下列各图中∠1和∠2是否为对顶角,并说明理由?
√
探究新知
∠ 2 +∠3= ,
你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3
180°
180°
由同角的补角相等可知
动动脑:为什么?
因此可得对顶角的性质:对顶角相等
探究新知
如图,直线AB、CD相交于-点O,
若∠1=28°,则∠2=_____.
28°
例题讲解
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
a
b
)
(
1
4
2
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
)
3
课堂练习
一、判断题(在正确的后面打“ ” ,在错误的后面打“ ”。)
(1)对顶角相等。 ( )
√
√
(2)相等的角是对顶角。 ( )
(3)有公共顶点且相等的两个角是对顶角。 ( )
(4)不相邻的两个角一定不是对顶角。 ( )
√
X
X
X
随堂练习
1.如图,直线AB与CD相交于点O,直线OE垂直直线CD,若∠ BOE=30°,则AOD的度数为( )
C
E
O
D
B
A
A.120 ° B.130 ° C.150 ° D.160 °
A
随堂练习
2.如图,直线AB与CD相交于点O,已知∠ AOD=165°,则∠ BOC的大小为( )
C
O
D
B
A
A.120 ° B.130 ° C.150 ° D.165 °
D
随堂练习
3.下面四个图形中,∠ 1与∠ 2是对顶角的为( )
C
1
2
1
2
1
2
1
2
A.
C.
B.
D.
拓展延伸
如图,直线AB、CD相交于点O,OA平分∠ EOC, ∠ EOC=60°,则∠ BOD的度数是多少度?
C
O
D
B
A
E
解:∵ OA平分∠ EOC, ∠ EOC=60°。 ∴ ∠ AOC=30°, (角平分线定义)
∴ ∠ BOD= ∠ AOC=60°(对顶角相等)
课堂小结
1.对顶角的概念:
一个角的两边是另一个角两边的反向延长线,具有这种位置 关系的两个角叫做对顶角。
2.互为邻补角的定义:
有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。
3.不重合的两条直线相交形成四个角邻补角的性质:
有四对邻补角,两对对顶角。
https://www.21cnjy.com/help/help_extract.php
