高中数学北师大版必修五课件 第三章 不等式习题课3 :34张PPT
文档属性
| 名称 | 高中数学北师大版必修五课件 第三章 不等式习题课3 :34张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 912.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 14:40:54 | ||
图片预览










文档简介
课件34张PPT。习题课 不等式的综合应用1.基础知识
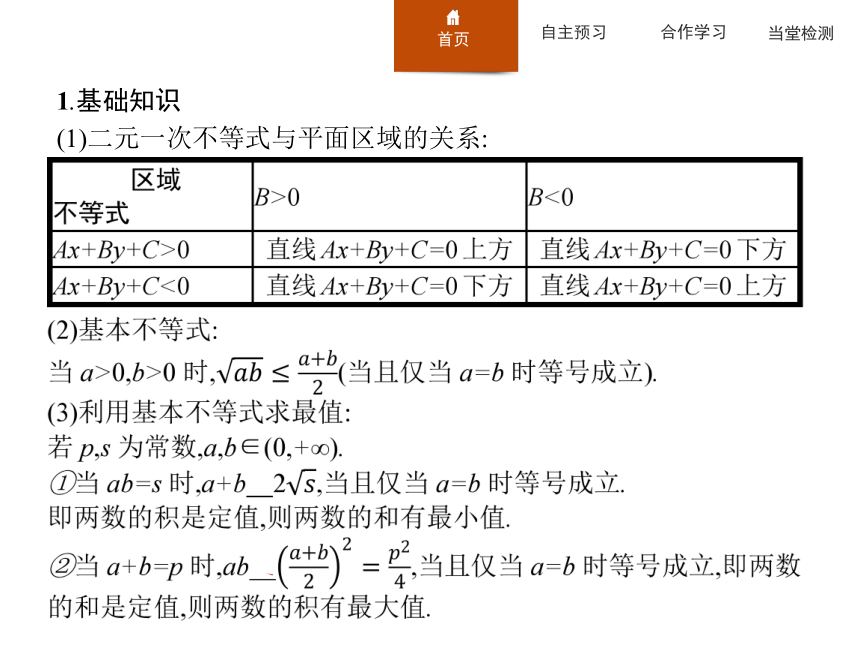
(1)二元一次不等式与平面区域的关系:【做一做1】(2016浙江高考)已知集合P={x∈R|1≤x≤3},Q={x∈R|x2≥4},则P∪(?RQ)=( )?
A.[2,3]
B.(-2,3]
C.[1,2)
D.(-∞,-2]∪[1,+∞)
解析:∵Q={x∈R|x2≥4}={x∈R|x≤-2或x≥2},
∴?RQ={x∈R|-2∴P∪(?RQ)={x∈R|-2答案:B若变量x,y满足约束条件 则z=2x+y的最大值和最小值分别为( )?
A.4和3 B.4和2
C.3和2 D.2和0
答案:B答案:C 【做一做2】 【做一做3】 探究一探究二探究三探究四思想方法
【例1】 求下列不等式的解集:
(1)-x2+8x-3>0;
(2)ax2-(a+1)x+1<0.
分析:(1)先将不等式变为标准形式x2-8x+3<0,再求解;
(2)对a要进行分类讨论,分a=0或a≠0两大类.
解:(1)原不等式可化为x2-8x+3<0,
又Δ=(-8)2-4×3=52>0,探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法反思感悟1.不含参的一元二次不等式解答时要注意将其化为标准形式,即ax2+bx+c>0(<0)(a>0)的形式.
2.含有参数的不等式的求解,往往需要对参数进行分类讨论.
(1)若二次项系数为常数,先确定二次项系数是否为正数,再考虑分解因式,对参数进行分类讨论,若不易分解因式,则可依据判别式符号进行分类讨论.
(2)若二次项系数为参数,则应先考虑二次项系数是否为零,确定不等式是否是二次不等式,再讨论二次项系数不为零的情形,以便确定解集的形式.探究一探究二探究三探究四思想方法变式训练1 探究一探究二探究三探究四思想方法
【例2】 (1)若4x+4y=1,则x+y的取值范围为 .?
(2)某楼盘的建筑成本由土地使用权费和材料工程费构成,已知土地使用权费为2 000元/m2,材料工程费在建造第一层时为400元/m2,以后每增加一层,费用增加40元/m2.要使平均每平方米建筑面积的成本费最低,则应把楼盘的楼房设计成 层.?探究一探究二探究三探究四思想方法答案:(1)(-∞,-1] (2)10 探究一探究二探究三探究四思想方法反思感悟1.应用基本不等式首先要验证是否符合条件.
2.应用基本不等式时不要忘记验证等号是否成立.
3.若是条件最值或范围问题,要选好突破口,注意围绕沟通所求与已知的联系为目的.
4.若条件不满足或不能直接套用基本不等式,可以考虑先将问题化归.探究一探究二探究三探究四思想方法变式训练2 (1)若正数x,y满足x+3y=5xy,则3x+4y的最小值是( )探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法解析:(1)在平面直角坐标系中作出不等式组所表示的平面区域,利用线性规划知识可得,在(2,0)处z取最小值,zmin=2,无最大值.探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法变式训练3 答案:C 探究一探究二探究三探究四思想方法
【例4】设函数f(x)=mx2-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;
(2)若对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.
解:(1)要使mx2-mx-1<0恒成立,
若m=0,显然-1<0;
?
?
所以-42.解决恒成立问题一定要搞清谁是主元,谁是参数,一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数.探究一探究二探究三探究四思想方法变式训练4 解:因为x∈[1,+∞)时, 恒成立,
即x2+2x+a>0恒成立.
即当x≥1时,a>-(x2+2x)=g(x)恒成立.
而g(x)=-(x2+2x)=-(x+1)2+1在[1,+∞)上是减少的,
所以g(x)max=g(1)=-3,故a>-3.
所以,实数a的取值范围是{a|a>-3}.探究一探究二探究三探究四思想方法转化与化归思想在不等式中的应用
【典例】 (1)已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞).若关于x的不等式f(x)(2)已知a∈[-1,1],不等式x2+(a-4)x+4-2a>0恒成立,则x的取值范围为 .?探究一探究二探究三探究四思想方法(2)把不等式的左端看成关于a的一次函数,记f(a)=(x-2)a+(x2-4x+4),
则由f(a)>0对于任意的a∈[-1,1]恒成立,易知只需f(-1)=x2-5x+6>0,且f(1)=x2-3x+2>0即可,联立解得x<1或x>3.
答案:(1)9 (2){x|x<1或x>3}探究一探究二探究三探究四思想方法方法点睛本题解法中利用了转化与化归思想.
(1)中利用“三个二次”之间的联系,将不等式、函数、方程之间相互转化.
(2)中将已知不等式看作关于a的一次不等式,体现了主元与次元的转化.利用转化与化归思想的原则是熟悉化原则、简单化原则、直观化原则、正难则反原则.探究一探究二探究三探究四思想方法变式训练 答案:C 12345解析:由x2-4x+3<0,解得1(1)若不等式的解集为{x|x<-3或x>-2},求k的值;
(2)若不等式的解集为?,求k的取值范围.
(1)二元一次不等式与平面区域的关系:【做一做1】(2016浙江高考)已知集合P={x∈R|1≤x≤3},Q={x∈R|x2≥4},则P∪(?RQ)=( )?
A.[2,3]
B.(-2,3]
C.[1,2)
D.(-∞,-2]∪[1,+∞)
解析:∵Q={x∈R|x2≥4}={x∈R|x≤-2或x≥2},
∴?RQ={x∈R|-2
A.4和3 B.4和2
C.3和2 D.2和0
答案:B答案:C 【做一做2】 【做一做3】 探究一探究二探究三探究四思想方法
【例1】 求下列不等式的解集:
(1)-x2+8x-3>0;
(2)ax2-(a+1)x+1<0.
分析:(1)先将不等式变为标准形式x2-8x+3<0,再求解;
(2)对a要进行分类讨论,分a=0或a≠0两大类.
解:(1)原不等式可化为x2-8x+3<0,
又Δ=(-8)2-4×3=52>0,探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法反思感悟1.不含参的一元二次不等式解答时要注意将其化为标准形式,即ax2+bx+c>0(<0)(a>0)的形式.
2.含有参数的不等式的求解,往往需要对参数进行分类讨论.
(1)若二次项系数为常数,先确定二次项系数是否为正数,再考虑分解因式,对参数进行分类讨论,若不易分解因式,则可依据判别式符号进行分类讨论.
(2)若二次项系数为参数,则应先考虑二次项系数是否为零,确定不等式是否是二次不等式,再讨论二次项系数不为零的情形,以便确定解集的形式.探究一探究二探究三探究四思想方法变式训练1 探究一探究二探究三探究四思想方法
【例2】 (1)若4x+4y=1,则x+y的取值范围为 .?
(2)某楼盘的建筑成本由土地使用权费和材料工程费构成,已知土地使用权费为2 000元/m2,材料工程费在建造第一层时为400元/m2,以后每增加一层,费用增加40元/m2.要使平均每平方米建筑面积的成本费最低,则应把楼盘的楼房设计成 层.?探究一探究二探究三探究四思想方法答案:(1)(-∞,-1] (2)10 探究一探究二探究三探究四思想方法反思感悟1.应用基本不等式首先要验证是否符合条件.
2.应用基本不等式时不要忘记验证等号是否成立.
3.若是条件最值或范围问题,要选好突破口,注意围绕沟通所求与已知的联系为目的.
4.若条件不满足或不能直接套用基本不等式,可以考虑先将问题化归.探究一探究二探究三探究四思想方法变式训练2 (1)若正数x,y满足x+3y=5xy,则3x+4y的最小值是( )探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法解析:(1)在平面直角坐标系中作出不等式组所表示的平面区域,利用线性规划知识可得,在(2,0)处z取最小值,zmin=2,无最大值.探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法探究一探究二探究三探究四思想方法变式训练3 答案:C 探究一探究二探究三探究四思想方法
【例4】设函数f(x)=mx2-mx-1.
(1)若对于一切实数x,f(x)<0恒成立,求m的取值范围;
(2)若对于x∈[1,3],f(x)<-m+5恒成立,求m的取值范围.
解:(1)要使mx2-mx-1<0恒成立,
若m=0,显然-1<0;
?
?
所以-4
即x2+2x+a>0恒成立.
即当x≥1时,a>-(x2+2x)=g(x)恒成立.
而g(x)=-(x2+2x)=-(x+1)2+1在[1,+∞)上是减少的,
所以g(x)max=g(1)=-3,故a>-3.
所以,实数a的取值范围是{a|a>-3}.探究一探究二探究三探究四思想方法转化与化归思想在不等式中的应用
【典例】 (1)已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞).若关于x的不等式f(x)
则由f(a)>0对于任意的a∈[-1,1]恒成立,易知只需f(-1)=x2-5x+6>0,且f(1)=x2-3x+2>0即可,联立解得x<1或x>3.
答案:(1)9 (2){x|x<1或x>3}探究一探究二探究三探究四思想方法方法点睛本题解法中利用了转化与化归思想.
(1)中利用“三个二次”之间的联系,将不等式、函数、方程之间相互转化.
(2)中将已知不等式看作关于a的一次不等式,体现了主元与次元的转化.利用转化与化归思想的原则是熟悉化原则、简单化原则、直观化原则、正难则反原则.探究一探究二探究三探究四思想方法变式训练 答案:C 12345解析:由x2-4x+3<0,解得1
(2)若不等式的解集为?,求k的取值范围.
