高中数学北师大版必修五课件 第三章 不等式3.4.2 :28张PPT
文档属性
| 名称 | 高中数学北师大版必修五课件 第三章 不等式3.4.2 :28张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 746.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 14:41:31 | ||
图片预览








文档简介
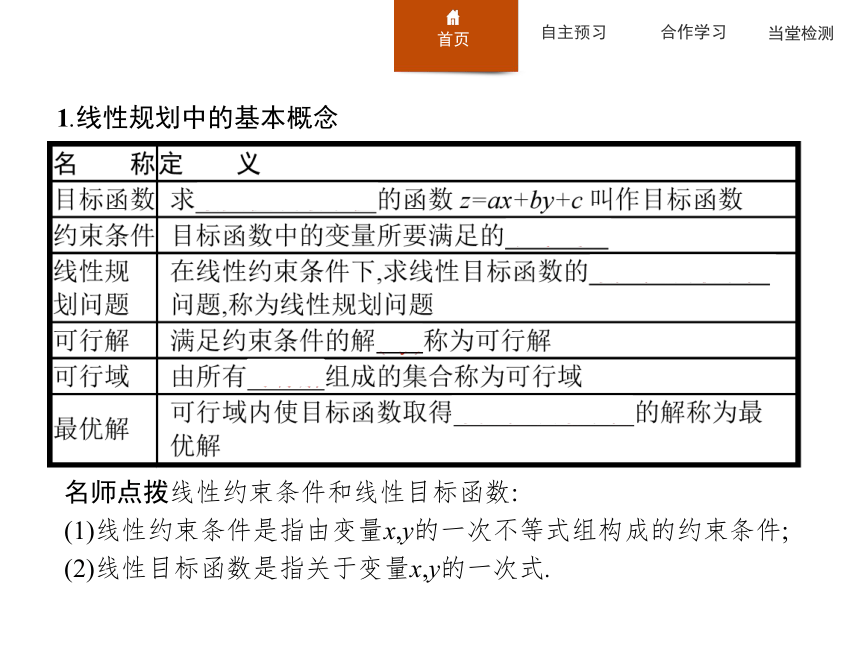
课件28张PPT。4.2 简单线性规划1.线性规划中的基本概念 名师点拨线性约束条件和线性目标函数:
(1)线性约束条件是指由变量x,y的一次不等式组构成的约束条件;
(2)线性目标函数是指关于变量x,y的一次式.2.简单的线性规划问题
(1)目标函数中y的系数大于0时的线性规划问题.
一般地,设目标函数为z=ax+by+c,当b>0时,把直线l0:ax+by=0向上平移时,所对应的z随之增大;把l0向下平移时,所对应的z随之减小.
由此可得到,在约束条件下,当b>0时,求目标函数的最大值或最小值的过程为:
①作出可行域;
②作出直线l0:ax+by=0;
③确定l0的平移方向,依可行域判断取得最优解的点;
④解相关方程组,求出最优解,从而得出目标函数的最小值或最大值.(2)目标函数中y的系数小于0时的线性规划问题.
一般地,在线性约束条件下,当b<0时,把直线ax+by=0向下平移时,z=ax+by+c的值增大;把直线ax+by=0向上平移时,z=ax+by+c的值减小.
由此可得到,在约束条件下,当b<0时,求目标函数的最大值或最小值的求解程序与b>0时相同,即为:
①作出可行域;
②作出直线l0:ax+by=0;
③确定l0的平移方向,依可行域判断取得最优解的点;
④解相关方程组,求出最优解,从而得出目标函数的最小值或最大值. 【做一做】目标函数z=2x-y,将其看成直线方程时,z的意义是( )?
A.该直线的截距
B.该直线的纵截距
C.该直线的纵截距的相反数
D.该直线的横截距
解析:z=2x-y可变形为y=2x-z,所以z的意义是该直线在y轴上截距的相反数.故选C.
答案:C归纳总结求解线性规划问题的基本步骤
在确定线性约束条件和线性目标函数的前提下,用图解法求最优解的步骤可概括为“画、移、求”,即:
(1)作图:在平面直角坐标系中,画出可行域和直线ax+by=0(目标函数为z=ax+by);
(2)平移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点;
(3)求值:求出使z取得最大值或最小值的点的坐标(解方程组)及z的最大值或最小值.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)约束条件是关于变量的不等式,其中次数必须为1. ( )
(2)线性目标函数的最优解一定是唯一的. ( )
(3)线性目标函数取得最值的点一定在可行域的顶点上. ( )
(4)目标函数z=ax+by(b≠0)中,z的几何意义是直线ax+by-z=0在y轴上的截距. ( )
答案:(1)× (2)× (3)× (4)×探究一探究二思维辨析试求:(1)z=4x-y的最大值;
(2)z=x-y的最小值;
(3)z=x+2y的最大值;
(4)z=x+y的最小值.探究一探究二思维辨析解:画出不等式组所对应的可行域(如图),由每条直线的方程可以求出A(1,1),B(2,4),C(3,5),D(5,5),E(5,3).探究一探究二思维辨析(1)令z=0,作出直线l1:4x-y=0,当直线l1向下平移时,函数值z随之增大,所以当l1经过点E时,z取最大值,且zmax=4×5-3=17.
(2)令z=0,作出直线l2:x-y=0,当直线l2向上平移时,函数值z随之减小,因为l2与直线x-y+2=0平行,所以当l2经过线段BC时,z取最小值,且zmin=3-5=-2.
(3)令z=0,作出直线l3:x+2y=0,当直线l3向上平移时,函数值z随之增大,所以当l3经过点D时,z取最大值,且zmax=5+5×2=15.
(4)令z=0,作出直线l4:x+y=0,当直线l4向下平移时,函数值z随之减小,所以当l4经过点A时,z取最小值,且zmin=1+1=2.探究一探究二思维辨析反思感悟1.求线性目标函数的最值问题,关键是准确地作出可行域,且要正确地把握目标函数的几何意义.一般步骤是:首先在平面直角坐标系内作出可行域;然后利用平移的方法在可行域内找到最优解所对应的点;最后将最优解代入目标函数求出最大值或最小值.
2.在目标函数z=ax+by中,若b>0,则向上平移时z增大,向下平移时z减小;若b<0,则向下平移时z增大,向上平移时z减小.探究一探究二思维辨析变式训练1 A.-7 B.-1 C.1 D.2
答案:A探究一探究二思维辨析分析:先画出不等式组所表示的平面区域,再根据各个目标函数的几何意义求解.探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析变式训练2 探究一探究二思维辨析解:作出可行域如图.
求出交点坐标分别为A(3,1),B(1,3),C(7,9).
(1)z=x2+y2-10y+25=x2+(y-5)2表示可行域内任意一点(x,y)到定点M(0,5)的距离的平方,过点M作BC的垂线,垂足为N,易知垂足N在线段BC上.探究一探究二思维辨析因作图出错导致结果错误 A.1,-1 B.2,-2 C.1,-2 D.2,-1
错解:作出可行域如图,设z=x+2y,作l0:x+2y=0,把l0向左下方平移到点(0,-1)时,z有最小值,zmin=-2.把l0向右上方移到(1,0)时,z有最大值,zmax=1.探究一探究二思维辨析正解:作出可行域(如图阴影部分),设z=x+2y,作l0:x+2y=0,把l0向左下方平移到点(0,-1)时,z有最小值,此时zmin=0+2×(-1)=-2.把l0向右上方平移到点(0,1)时,z有最大值,此时zmax=0+2×1=2.
答案:B探究一探究二思维辨析纠错心得1.对于线性规划问题,正确作出可行域是解决问题的基础.
2.对于可行域边界的虚实,及线性目标函数中直线的斜率与可行域中直线的斜率的比较是问题的核心.
3.对于本题来说,未能分析好x+2y=0的斜率与x+y=1的斜率大小关系,导致画图出错.12345解析:设x+y=b,则y=-x+b,画出可行域,如图阴影部分.
利用图解法,知当直线y=-x+b过点M时,b取最小值.答案:C 12345解析:根据不等式组,作出可行域,如图△ABC内部及边界.
画直线l0:3x-y=0,平行移动l0到直线l的位置,经过可行域内点C时,目标函数z取到最大值.因此,当x=2,y=2时,z取最大值,zmax=3×2-2=4.
答案:D1234512345解析:如图所示,画出不等式组所表示的区域,作直线l:mx+y=0,m∈[2,4],可知当x=2,y=1时,zmax=2m+1∈[5,9].答案:[5,9] 12345解:画出不等式组表示的可行域如图阴影部分,
(1)线性约束条件是指由变量x,y的一次不等式组构成的约束条件;
(2)线性目标函数是指关于变量x,y的一次式.2.简单的线性规划问题
(1)目标函数中y的系数大于0时的线性规划问题.
一般地,设目标函数为z=ax+by+c,当b>0时,把直线l0:ax+by=0向上平移时,所对应的z随之增大;把l0向下平移时,所对应的z随之减小.
由此可得到,在约束条件下,当b>0时,求目标函数的最大值或最小值的过程为:
①作出可行域;
②作出直线l0:ax+by=0;
③确定l0的平移方向,依可行域判断取得最优解的点;
④解相关方程组,求出最优解,从而得出目标函数的最小值或最大值.(2)目标函数中y的系数小于0时的线性规划问题.
一般地,在线性约束条件下,当b<0时,把直线ax+by=0向下平移时,z=ax+by+c的值增大;把直线ax+by=0向上平移时,z=ax+by+c的值减小.
由此可得到,在约束条件下,当b<0时,求目标函数的最大值或最小值的求解程序与b>0时相同,即为:
①作出可行域;
②作出直线l0:ax+by=0;
③确定l0的平移方向,依可行域判断取得最优解的点;
④解相关方程组,求出最优解,从而得出目标函数的最小值或最大值. 【做一做】目标函数z=2x-y,将其看成直线方程时,z的意义是( )?
A.该直线的截距
B.该直线的纵截距
C.该直线的纵截距的相反数
D.该直线的横截距
解析:z=2x-y可变形为y=2x-z,所以z的意义是该直线在y轴上截距的相反数.故选C.
答案:C归纳总结求解线性规划问题的基本步骤
在确定线性约束条件和线性目标函数的前提下,用图解法求最优解的步骤可概括为“画、移、求”,即:
(1)作图:在平面直角坐标系中,画出可行域和直线ax+by=0(目标函数为z=ax+by);
(2)平移:平行移动直线ax+by=0,确定使z=ax+by取得最大值或最小值的点;
(3)求值:求出使z取得最大值或最小值的点的坐标(解方程组)及z的最大值或最小值.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)约束条件是关于变量的不等式,其中次数必须为1. ( )
(2)线性目标函数的最优解一定是唯一的. ( )
(3)线性目标函数取得最值的点一定在可行域的顶点上. ( )
(4)目标函数z=ax+by(b≠0)中,z的几何意义是直线ax+by-z=0在y轴上的截距. ( )
答案:(1)× (2)× (3)× (4)×探究一探究二思维辨析试求:(1)z=4x-y的最大值;
(2)z=x-y的最小值;
(3)z=x+2y的最大值;
(4)z=x+y的最小值.探究一探究二思维辨析解:画出不等式组所对应的可行域(如图),由每条直线的方程可以求出A(1,1),B(2,4),C(3,5),D(5,5),E(5,3).探究一探究二思维辨析(1)令z=0,作出直线l1:4x-y=0,当直线l1向下平移时,函数值z随之增大,所以当l1经过点E时,z取最大值,且zmax=4×5-3=17.
(2)令z=0,作出直线l2:x-y=0,当直线l2向上平移时,函数值z随之减小,因为l2与直线x-y+2=0平行,所以当l2经过线段BC时,z取最小值,且zmin=3-5=-2.
(3)令z=0,作出直线l3:x+2y=0,当直线l3向上平移时,函数值z随之增大,所以当l3经过点D时,z取最大值,且zmax=5+5×2=15.
(4)令z=0,作出直线l4:x+y=0,当直线l4向下平移时,函数值z随之减小,所以当l4经过点A时,z取最小值,且zmin=1+1=2.探究一探究二思维辨析反思感悟1.求线性目标函数的最值问题,关键是准确地作出可行域,且要正确地把握目标函数的几何意义.一般步骤是:首先在平面直角坐标系内作出可行域;然后利用平移的方法在可行域内找到最优解所对应的点;最后将最优解代入目标函数求出最大值或最小值.
2.在目标函数z=ax+by中,若b>0,则向上平移时z增大,向下平移时z减小;若b<0,则向下平移时z增大,向上平移时z减小.探究一探究二思维辨析变式训练1 A.-7 B.-1 C.1 D.2
答案:A探究一探究二思维辨析分析:先画出不等式组所表示的平面区域,再根据各个目标函数的几何意义求解.探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析探究一探究二思维辨析变式训练2 探究一探究二思维辨析解:作出可行域如图.
求出交点坐标分别为A(3,1),B(1,3),C(7,9).
(1)z=x2+y2-10y+25=x2+(y-5)2表示可行域内任意一点(x,y)到定点M(0,5)的距离的平方,过点M作BC的垂线,垂足为N,易知垂足N在线段BC上.探究一探究二思维辨析因作图出错导致结果错误 A.1,-1 B.2,-2 C.1,-2 D.2,-1
错解:作出可行域如图,设z=x+2y,作l0:x+2y=0,把l0向左下方平移到点(0,-1)时,z有最小值,zmin=-2.把l0向右上方移到(1,0)时,z有最大值,zmax=1.探究一探究二思维辨析正解:作出可行域(如图阴影部分),设z=x+2y,作l0:x+2y=0,把l0向左下方平移到点(0,-1)时,z有最小值,此时zmin=0+2×(-1)=-2.把l0向右上方平移到点(0,1)时,z有最大值,此时zmax=0+2×1=2.
答案:B探究一探究二思维辨析纠错心得1.对于线性规划问题,正确作出可行域是解决问题的基础.
2.对于可行域边界的虚实,及线性目标函数中直线的斜率与可行域中直线的斜率的比较是问题的核心.
3.对于本题来说,未能分析好x+2y=0的斜率与x+y=1的斜率大小关系,导致画图出错.12345解析:设x+y=b,则y=-x+b,画出可行域,如图阴影部分.
利用图解法,知当直线y=-x+b过点M时,b取最小值.答案:C 12345解析:根据不等式组,作出可行域,如图△ABC内部及边界.
画直线l0:3x-y=0,平行移动l0到直线l的位置,经过可行域内点C时,目标函数z取到最大值.因此,当x=2,y=2时,z取最大值,zmax=3×2-2=4.
答案:D1234512345解析:如图所示,画出不等式组所表示的区域,作直线l:mx+y=0,m∈[2,4],可知当x=2,y=1时,zmax=2m+1∈[5,9].答案:[5,9] 12345解:画出不等式组表示的可行域如图阴影部分,
