2020沪科版九年级数学下册课件:解题技巧专题:求不规则阴影部分的面积(共15张PPT)
文档属性
| 名称 | 2020沪科版九年级数学下册课件:解题技巧专题:求不规则阴影部分的面积(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-19 19:37:36 | ||
图片预览


文档简介
(共32张PPT)
解题技巧专题
求不规则阴影部分的面积
全面掌握核心方法,以不变应万变
◆类型一直接利用规则图形的和差求面积
1.(2019·吉林中考)如图,在扇形OAB中,∠AOB=
90.D,E分别是半径OA,OB上的点,以OD,OE为邻
边的□ODCE的顶点C在AB上若OD=8,OE=6,则
阴影部分图形的面积是25π-48(结果保留π)
B
E
D A
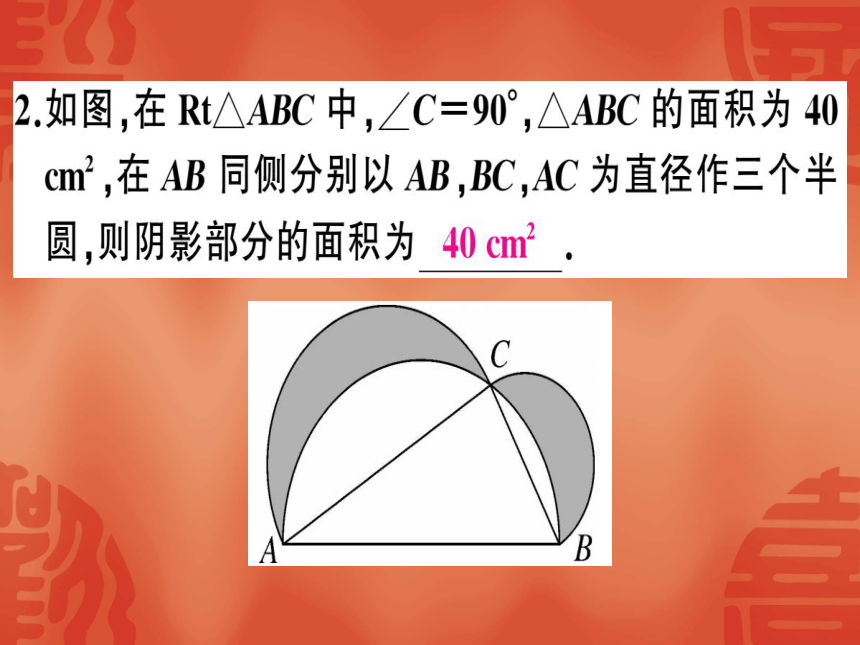
2如图,在Rt△ABC中,∠C=90°,△ABC的面积为40
cm2,在AB同侧分别以AB,BC,AC为直径作三个半
圆,则阴影部分的面积为40cm2.
C
B
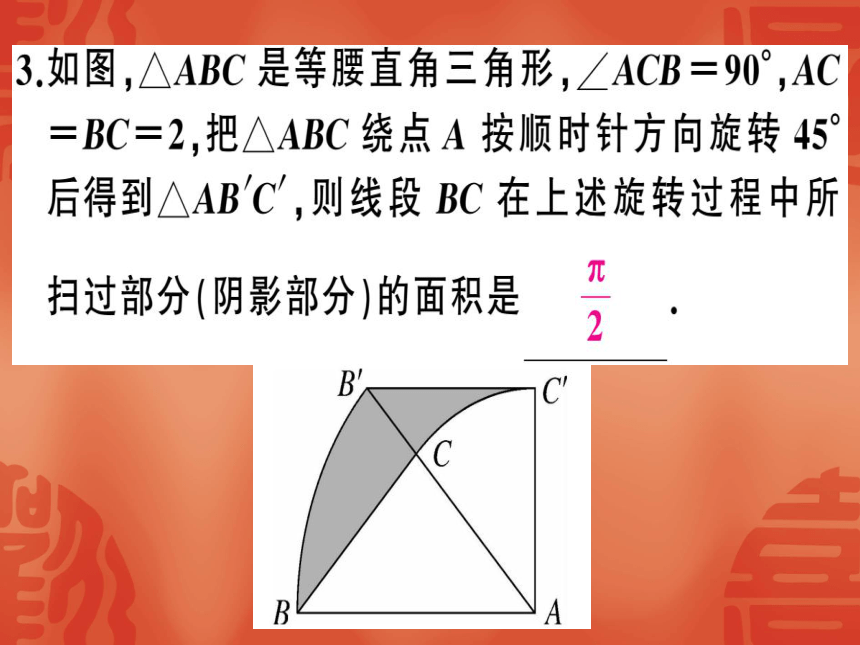
3如图,△ABC是等腰直角三角形,∠ACB=90°,AC
=BC=2,把△ABC绕点A按顺时针方向旋转45°
后得到△ABC',则线段BC在上述旋转过程中所
扫过部分(阴影部分)的面积是2
B
C
B
A
类型二割补法
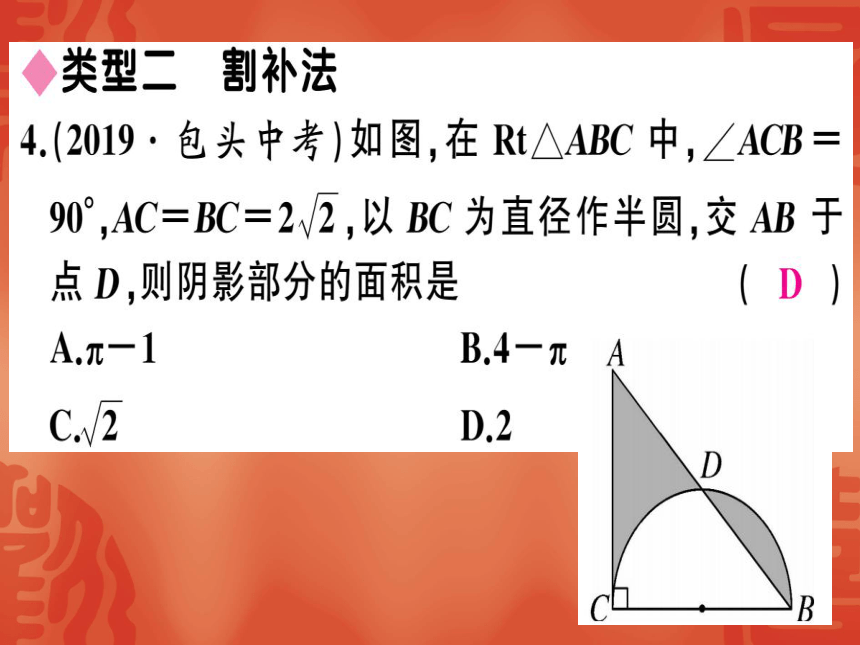
4.(2019·包头中考)如图,在Rt△ABC中,∠ACB
90°,AC=BC=22,以BC为直径作半圆,交AB于
点D,则阴影部分的面积是
B.4-兀
D,2
B
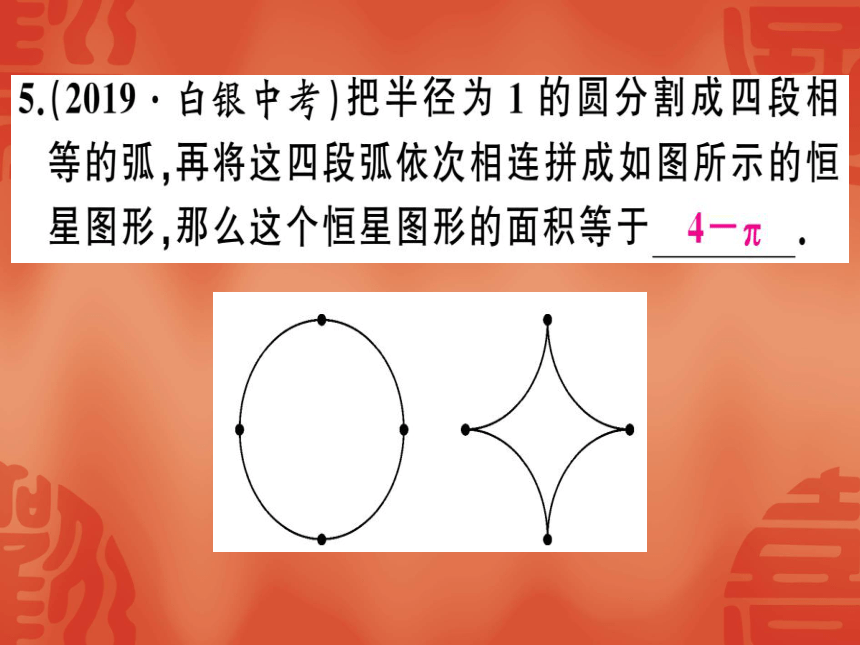
5(2019·白银中考)把半径为1的圆分割成四段相
等的弧,再将这四段弧依次相连拼成如图所示的恒
星图形,那么这个恒星图形的面积等于4-π
人
◆类型三等积法
轴对称、旋转
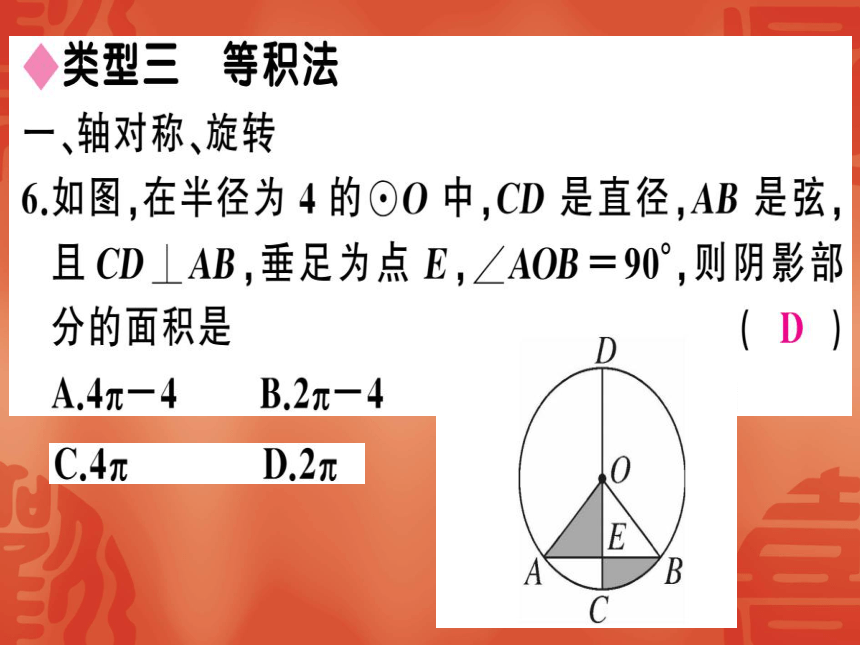
6如图,在半径为4的⊙O中,CD是直径,AB是弦,
且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部
分的面积是
A4兀-4
B.2兀-4
C.4兀
D.2兀
B
7如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,
点D为AB的中点,以点D为圆心作圆心角为90
的扇形DEF,点C恰在弧EF上,则图中阴影部分
的面积为
(D
×、c
2
B.兀4
心2
4
C
2
A-+
B.兀
G
A
H
E
【解析】如图,连接CD,作DM⊥BC于点M,DN⊥AC于点
N.∴CA=CB,∠ACB=90°,AB=2,点D为AB的中点,
∴DC-2AB=1,CD平分∠BCA.∴DM=DN,四边形
2
DMCN是正方形,DM=.则扇形DEF的面积是
90x×12
3604·∠GDH=∠MDN=90,∴∠GDM=
∠DMG=∠DNH,
∠HDN在△DMG和△DNH中,DM=DN,
∠GDM=∠HDN,
△DMG≌△DNH(ASA).∴S四边形DCH=S正方形DMN=
2
则阴影部分的面积是
故选D
42
A
H
N
解题技巧专题
求不规则阴影部分的面积
全面掌握核心方法,以不变应万变
◆类型一直接利用规则图形的和差求面积
1.(2019·吉林中考)如图,在扇形OAB中,∠AOB=
90.D,E分别是半径OA,OB上的点,以OD,OE为邻
边的□ODCE的顶点C在AB上若OD=8,OE=6,则
阴影部分图形的面积是25π-48(结果保留π)
B
E
D A
2如图,在Rt△ABC中,∠C=90°,△ABC的面积为40
cm2,在AB同侧分别以AB,BC,AC为直径作三个半
圆,则阴影部分的面积为40cm2.
C
B
3如图,△ABC是等腰直角三角形,∠ACB=90°,AC
=BC=2,把△ABC绕点A按顺时针方向旋转45°
后得到△ABC',则线段BC在上述旋转过程中所
扫过部分(阴影部分)的面积是2
B
C
B
A
类型二割补法
4.(2019·包头中考)如图,在Rt△ABC中,∠ACB
90°,AC=BC=22,以BC为直径作半圆,交AB于
点D,则阴影部分的面积是
B.4-兀
D,2
B
5(2019·白银中考)把半径为1的圆分割成四段相
等的弧,再将这四段弧依次相连拼成如图所示的恒
星图形,那么这个恒星图形的面积等于4-π
人
◆类型三等积法
轴对称、旋转
6如图,在半径为4的⊙O中,CD是直径,AB是弦,
且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部
分的面积是
A4兀-4
B.2兀-4
C.4兀
D.2兀
B
7如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,
点D为AB的中点,以点D为圆心作圆心角为90
的扇形DEF,点C恰在弧EF上,则图中阴影部分
的面积为
(D
×、c
2
B.兀4
心2
4
C
2
A-+
B.兀
G
A
H
E
【解析】如图,连接CD,作DM⊥BC于点M,DN⊥AC于点
N.∴CA=CB,∠ACB=90°,AB=2,点D为AB的中点,
∴DC-2AB=1,CD平分∠BCA.∴DM=DN,四边形
2
DMCN是正方形,DM=.则扇形DEF的面积是
90x×12
3604·∠GDH=∠MDN=90,∴∠GDM=
∠DMG=∠DNH,
∠HDN在△DMG和△DNH中,DM=DN,
∠GDM=∠HDN,
△DMG≌△DNH(ASA).∴S四边形DCH=S正方形DMN=
2
则阴影部分的面积是
故选D
42
A
H
N
