人教版九年级数学上册课件:22.3实际问题与二次函数(共20张PPT)
文档属性
| 名称 | 人教版九年级数学上册课件:22.3实际问题与二次函数(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 913.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-20 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
基础回顾 什么叫函数?
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数, x叫自变量
目前,我们已经学习了那几种类型的函数?
函 数
一次函数y=kx+b (k≠0)
二次函数 (a≠0)
22.3 实际问题与二次函数
师友探究
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l的值.
矩形场地的周长是60m,一边长为l,则另一边长
为 m,场地的面积:
S=l(30-l)
即S=-l2+30l. (0
请同学们观察此函数的图象
师友探究
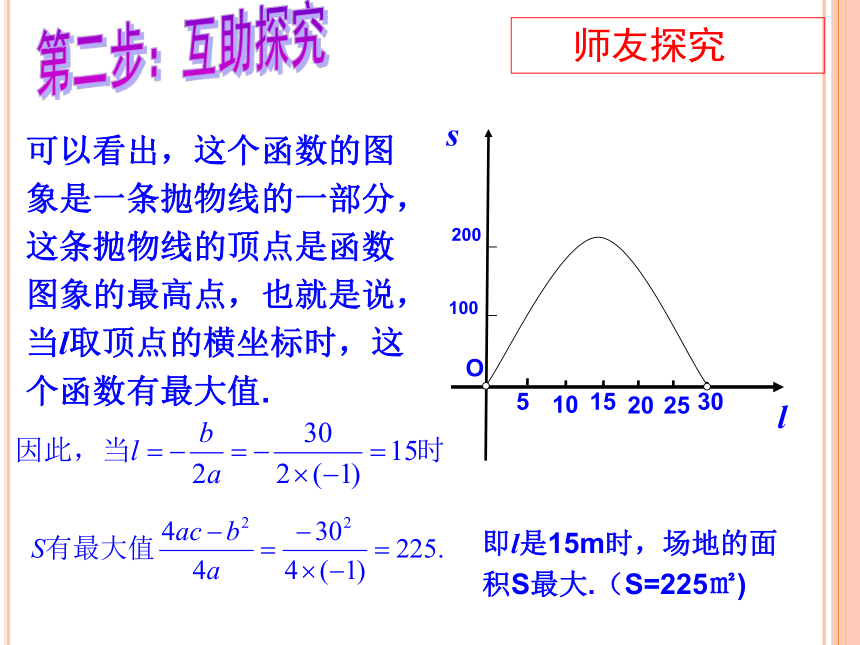
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.
即l是15m时,场地的面积S最大.(S=225㎡)
O
师友探究
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以当 时,二次函数y=ax2+bx+c有最小(大)值 .
但由于受自变量x求值范围的影响,往往要把一般式转化为顶点式思考更为直观。
师友探究
问题2.已知某商品的进价为每件40元。现在
的售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格?,每涨价一元,
每星期要少卖出10件;每降价一元,每星期
可多卖出20件。如何定价才能使利润最大?
请同学们带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
师友探究
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y与x的函数关系式.涨
价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
y=(60+x-40)(300-10x)
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6250
怎样确定x的取值范围
定价:60+5=65(元)
师友探究
解:设每件降价x元时的总利润为y元.
y=(60-40-x)(300+20x)
=(20-x)(300+20x)
=-20x2+100x+6000
=-20(x2-5x-300)
=-20(x-2.5)2+6125 (0≤x≤20)
所以定价为60-2.5=57.5时利润最大,最大值为6125元.
答:综合以上两种情况,定价为65元时可
获得最大利润为6250元.
怎样确定x的取值范围
师友探究
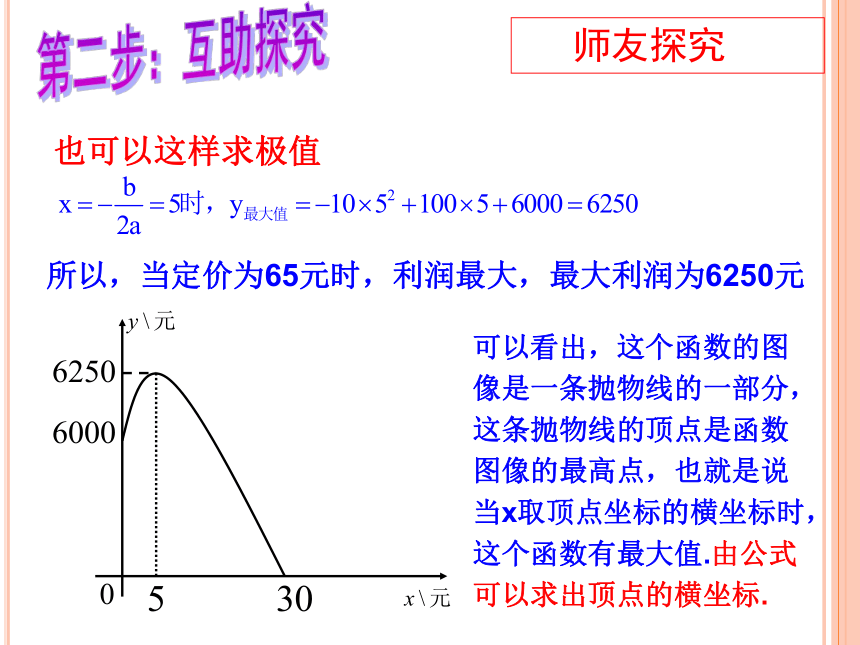
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元
也可以这样求极值
师友探究
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
解决这类题目的一般步骤
师友探究
解一
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-3,这时有:
解二
如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
当水面下降1m时,水面的纵坐标为y=-1,这时有:
此时,抛物线的顶点为(0,2)
解三
如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
师友探究
解决这类题目的一般步骤
1.根据题意建立平面直角坐标系。
2.把已知数据转化为点坐标。
3.利用点坐标求二次函数解析式。
4.利用二次函数解析式解决实际问题。
师友训练
某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
1.这节课你收获了哪些知识?
2.你有哪些要注意的问题?
3.你(你的学友)表现怎样?
师友总结
友情提示:师傅指导学友从知识、学法和师友互助方面进行全面总结。
教师归纳
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
二次函数解决实际问题的一般步骤
评一评这节课的最佳师友
布置作业
巩固作业:练习册
预习作业:
教师评价
帮助别人就是帮助自己!
和谐互助,师友共赢!
基础回顾 什么叫函数?
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,另一个变量y总有唯一的值与它对应。
这样的两个变量之间的关系我们把它叫做函数关系。
对于上述变量x 、y,我们把y叫x的函数, x叫自变量
目前,我们已经学习了那几种类型的函数?
函 数
一次函数y=kx+b (k≠0)
二次函数 (a≠0)
22.3 实际问题与二次函数
师友探究
问题1:用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少时,场地的面积S最大?
分析:先写出S与l的函数关系式,再求出使S最大的l的值.
矩形场地的周长是60m,一边长为l,则另一边长
为 m,场地的面积:
S=l(30-l)
即S=-l2+30l. (0
请同学们观察此函数的图象
师友探究
可以看出,这个函数的图象是一条抛物线的一部分,这条抛物线的顶点是函数图象的最高点,也就是说,当l取顶点的横坐标时,这个函数有最大值.
即l是15m时,场地的面积S最大.(S=225㎡)
O
师友探究
一般地,因为抛物线y=ax2+bx+c的顶点是最低(高)点,所以当 时,二次函数y=ax2+bx+c有最小(大)值 .
但由于受自变量x求值范围的影响,往往要把一般式转化为顶点式思考更为直观。
师友探究
问题2.已知某商品的进价为每件40元。现在
的售价是每件60元,每星期可卖出300件。
市场调查反映:如调整价格?,每涨价一元,
每星期要少卖出10件;每降价一元,每星期
可多卖出20件。如何定价才能使利润最大?
请同学们带着以下几个问题读题
(1)题目中有几种调整价格的方法?
(2)题目涉及到哪些变量?哪一个量是自变量?哪些量随之发生了变化?
师友探究
分析:
调整价格包括涨价和降价两种情况
先来看涨价的情况:⑴设每件涨价x元,则每星期售出商品
的利润y也随之变化,我们先来确定y与x的函数关系式.涨
价x元,则每星期少卖 件,实际卖出 件,
每件利润为 元,因此,所得利润
为 元.
10x
(300-10x)
(60+x-40)
(60+x-40)(300-10x)
y=(60+x-40)(300-10x)
(0≤x≤30)
即y=-10(x-5)2+6250
∴当x=5时,y最大值=6250
怎样确定x的取值范围
定价:60+5=65(元)
师友探究
解:设每件降价x元时的总利润为y元.
y=(60-40-x)(300+20x)
=(20-x)(300+20x)
=-20x2+100x+6000
=-20(x2-5x-300)
=-20(x-2.5)2+6125 (0≤x≤20)
所以定价为60-2.5=57.5时利润最大,最大值为6125元.
答:综合以上两种情况,定价为65元时可
获得最大利润为6250元.
怎样确定x的取值范围
师友探究
可以看出,这个函数的图像是一条抛物线的一部分,这条抛物线的顶点是函数图像的最高点,也就是说当x取顶点坐标的横坐标时,这个函数有最大值.由公式可以求出顶点的横坐标.
所以,当定价为65元时,利润最大,最大利润为6250元
也可以这样求极值
师友探究
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
解决这类题目的一般步骤
师友探究
解一
∴可设这条抛物线所表示的二次函数的解析式为:
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的二次函数为:
当水面下降1m时,水面的纵坐标为y=-3,这时有:
解二
如图所示,以抛物线和水面的两个交点的连线为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系.
当水面下降1m时,水面的纵坐标为y=-1,这时有:
此时,抛物线的顶点为(0,2)
解三
如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
师友探究
解决这类题目的一般步骤
1.根据题意建立平面直角坐标系。
2.把已知数据转化为点坐标。
3.利用点坐标求二次函数解析式。
4.利用二次函数解析式解决实际问题。
师友训练
某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
1.这节课你收获了哪些知识?
2.你有哪些要注意的问题?
3.你(你的学友)表现怎样?
师友总结
友情提示:师傅指导学友从知识、学法和师友互助方面进行全面总结。
教师归纳
(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;
(2)在自变量的取值范围内,运用公式法或通过配方求出二次函数的最大值或最小值.
二次函数解决实际问题的一般步骤
评一评这节课的最佳师友
布置作业
巩固作业:练习册
预习作业:
教师评价
帮助别人就是帮助自己!
和谐互助,师友共赢!
同课章节目录
