3.4 实际问题与一元一次方程(方案与择优问题)课件
文档属性
| 名称 | 3.4 实际问题与一元一次方程(方案与择优问题)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-20 07:02:40 | ||
图片预览







文档简介
(共24张PPT)
人教版 七上
3.4实际问题与一元一次方程
(方案与择优问题)
教学重点:利用数学对生活中的计费、旅游等进行优化选择。
教学难点:分类讨论方案的理解与运用。
教学重、难点
佩奇、乔治等小朋友随家长一同到某公园游玩,下面是购买门票时,佩奇与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)佩奇他们一共去了几个成人,几个小孩?
(2)请你帮助佩奇算一算,用哪种方式购票更省钱?
情境引入
解:设成人人数为x人则小孩人数为(12-x) 人,根据题意可得
60x+ (12-x) =600
60x+ 360-30x =600
30x =240
x =8
小孩人数为(12-x)=12-8=4(人)
答:成人人数为8人,小孩人数为4人.
探究新知
(2)如果买团体票,按16人计算,共需费用:
60 ×0.6 ×16=576(元)
∵576<600
∴购买团体票更省钱.
探究新知
一家三人(父母、女儿)准备参加旅游团外出旅游,甲旅行社告知:“父母买全票,女儿按半价优惠”.乙旅行社告知:“家庭旅行按团体票计价,即每人按全价的八折收费”.若两家旅行社每人票价相同,那么更优惠的是( )
A.甲 B.乙 C.甲乙相同 D.不能确定
分析:设每人票价为x元,则甲优惠后全家票价为2.5x元,乙优惠后全家票价为2.4x,故乙旅行社更优惠.
B
练一练
探究新知
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用费(元)
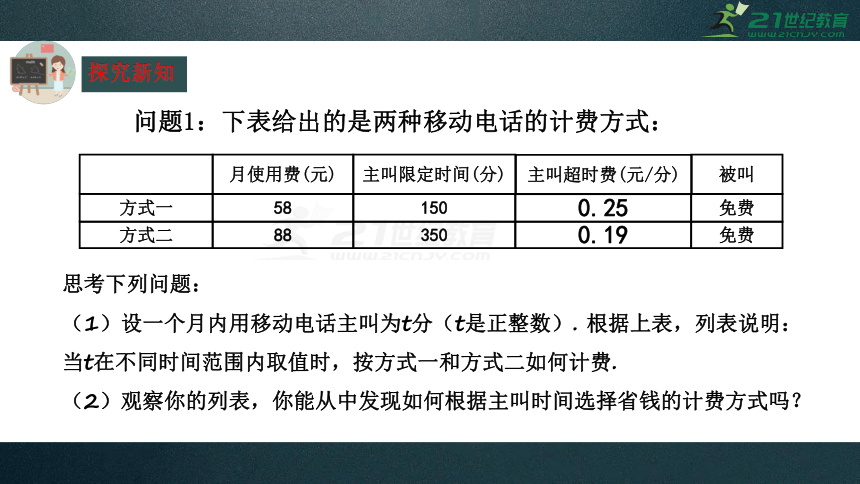
问题1:下表给出的是两种移动电话的计费方式:
思考下列问题:
(1)设一个月内用移动电话主叫为t分(t是正整数). 根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
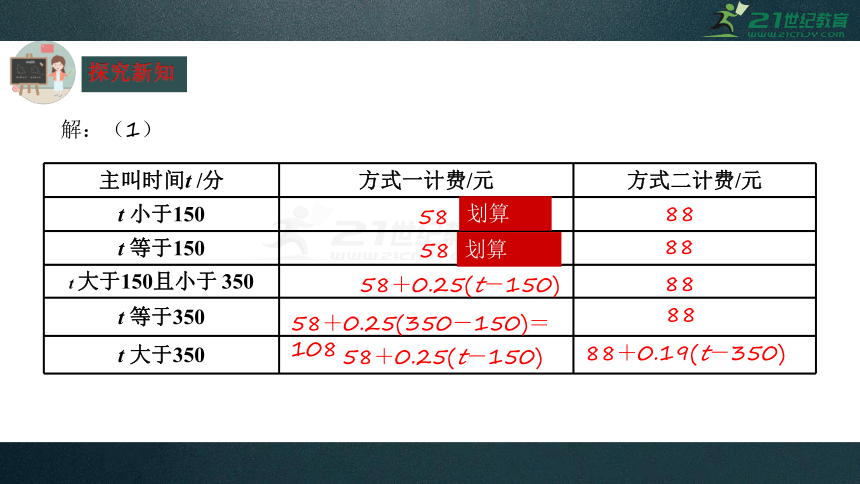
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
解:(1)
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88+0.19(t-350)
划算
划算
探究新知
由题意可得
t小于或等于150时,方式一的付 费为58元,而方式二的付费为88元.
因为58<88
所以方式一计费省钱;
150当58+0.25(t-150) = 88时
解得t =270
t<270时,方式一省钱t=270时,两种方式一样省钱, 270探究新知
t ≧ 350时,0.25t+20.5-(0.19t+21.5)=0.006-1>0,方式二省钱.
综上所述,
t<270时,方式一省钱
t=270时,两种方式一样省钱
t>270时,方式二省钱.
探究新知
1.某电信局现有两种通讯业务:快捷通,无月租费,每分钟的通话费为0.20元;全球通,月租费15元,每分钟的通话费为0.10元.小李每月的通话时间大约为300分钟,则他应选择( )
A.快捷通 B.全球通
C.两种一样 D.不能确定
B
练一练
某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨利润为500元;制成酸奶后销售,每吨利润高达1200元;制成奶片后销售,每吨利润获得2000元,当地一家公司收购这种蔬菜140吨,该工厂的加工能力是:
制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨.受人员限制,但两种方式不能同时进行.受气温等条件限制,公司必须在4天内将这批鲜奶全部销售或加工完毕。
(1)请你为此公司研制三种可行方案;
(1)你认为选择哪种方案获利最多?为什么?
探究新知
解:(1)
方案一:将鲜奶全部直接销售.
方案二:尽可能地对鲜奶制成奶片,没有来得及进行加工的鲜奶直接在市场销售.
方案三:将鲜奶部件制成奶片,其余鲜奶制成酸奶,并恰好4天完成.
(2)
方案一:获利为9 ×500=4500(元)
方案二:4天制成酸奶4 ×1=4(吨),还有5吨需要在市场直接销售,
获利为9 ×500=4500(元)
探究新知
方案三:设制成酸片x吨,制成酸奶(9-x)吨,根据题意,得
∴获利为1200 ×7.5+2000 × 2=12000(元)
答:选择方案三获利最多.
探究新知
例题小结
(1)弄清题意
(2)找准题中的等量关系.
(3)设出未知数.
(2)解出方程并答题.
1.小明和小红一起拼购购买相同的学习机,甲店承诺若一次购买两台学习机,其中台按原价而另一台可获得七折优惠,乙店承诺若一次购买两台学习机,按总价的80%收费,在哪家店购买学习更优惠( )
乙比甲优惠 B. 甲比乙优惠
C. 甲乙一样 D. 以上都有可能
A
课堂练习
课堂练习
2.甲乙两家手机店出售某型号定价相同的手机,甲店手机连续降价15%,乙店手机一次降价30%,在哪家手机店购买手机更合算( )
A.甲 B. 乙 C. 甲乙一样 D与价格有关
B
课堂练习
3.某公园的门票价格规定如下表:
购票人数 1—50人 51—100人 100人以上
每人门票价 25 23 21
公学校七年级(1)、 (2)两班共有104名学生去公园游玩,其中甲班的人数少于50人,乙班的人数多于50人,若两班都以班为单位分别购票,则共需付款2488元。问:
(1)两班各有多少个学生?
(2)怎样购票最为划算?
解:(1)设甲班有x个学生,则乙班有(104-x)个学生,根据题意得
13x +(104-x)=2488
解得x =48
所以104-x =56
答:甲班有48个学生,则乙班有56个学生.
(2)两班都以班为单位分别购票,则共需付款2488元。若两班作为一个团体购票:
104×21=2184(元)
2488-2184=304(元)
答:两班作为一个团体购票最为划算,可以省了304元
课堂练习
课堂练习
4.某市剧院举办大型文艺演出,其门票价格为:一等席300元/人,二等席200元/人,三等席150元/人,某公司组织36名员工去观看,计划用5850元购买2种门票,请你帮助公司设计可能的购票方案.
(1)设买一等席门票x张,则买二等席门票(36-x)张,根据题意,得
300x+200(36-x)=5 850,
解得x=-13.5,
票数不能为负数,不符题意,舍去.
(2)设买二等席门票y张,则买三等席门票(36-y)张.根据题意,得200y+150(36-y)=5 850,
解得y=9,所以36-9=27.
(3)设买一等席门票z张,则三等席门票(36-z)张.根据题意,得300z+150(36-z)=5 850,
解得z=3,所以36-3=33.
综上,共有两种方案:
买二等席门票9张,三等席门票27张或买一等席门票3张,三等席门票33张.
课堂练习
谈谈你们这节课有什么收获呢?
1策略问题
2电话计费问题
3方案设计问题
课堂小结
第106页
练习第2、3题
课外作业
https://www.21cnjy.com/help/help_extract.php
人教版 七上
3.4实际问题与一元一次方程
(方案与择优问题)
教学重点:利用数学对生活中的计费、旅游等进行优化选择。
教学难点:分类讨论方案的理解与运用。
教学重、难点
佩奇、乔治等小朋友随家长一同到某公园游玩,下面是购买门票时,佩奇与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
(1)佩奇他们一共去了几个成人,几个小孩?
(2)请你帮助佩奇算一算,用哪种方式购票更省钱?
情境引入
解:设成人人数为x人则小孩人数为(12-x) 人,根据题意可得
60x+ (12-x) =600
60x+ 360-30x =600
30x =240
x =8
小孩人数为(12-x)=12-8=4(人)
答:成人人数为8人,小孩人数为4人.
探究新知
(2)如果买团体票,按16人计算,共需费用:
60 ×0.6 ×16=576(元)
∵576<600
∴购买团体票更省钱.
探究新知
一家三人(父母、女儿)准备参加旅游团外出旅游,甲旅行社告知:“父母买全票,女儿按半价优惠”.乙旅行社告知:“家庭旅行按团体票计价,即每人按全价的八折收费”.若两家旅行社每人票价相同,那么更优惠的是( )
A.甲 B.乙 C.甲乙相同 D.不能确定
分析:设每人票价为x元,则甲优惠后全家票价为2.5x元,乙优惠后全家票价为2.4x,故乙旅行社更优惠.
B
练一练
探究新知
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用费(元)
问题1:下表给出的是两种移动电话的计费方式:
思考下列问题:
(1)设一个月内用移动电话主叫为t分(t是正整数). 根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费.
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
解:(1)
58
88
58
88
88
88
58+0.25(t-150)
58+0.25(350-150)=108
58+0.25(t-150)
88+0.19(t-350)
划算
划算
探究新知
由题意可得
t小于或等于150时,方式一的付 费为58元,而方式二的付费为88元.
因为58<88
所以方式一计费省钱;
150
解得t =270
t<270时,方式一省钱t=270时,两种方式一样省钱, 270
t ≧ 350时,0.25t+20.5-(0.19t+21.5)=0.006-1>0,方式二省钱.
综上所述,
t<270时,方式一省钱
t=270时,两种方式一样省钱
t>270时,方式二省钱.
探究新知
1.某电信局现有两种通讯业务:快捷通,无月租费,每分钟的通话费为0.20元;全球通,月租费15元,每分钟的通话费为0.10元.小李每月的通话时间大约为300分钟,则他应选择( )
A.快捷通 B.全球通
C.两种一样 D.不能确定
B
练一练
某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨利润为500元;制成酸奶后销售,每吨利润高达1200元;制成奶片后销售,每吨利润获得2000元,当地一家公司收购这种蔬菜140吨,该工厂的加工能力是:
制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨.受人员限制,但两种方式不能同时进行.受气温等条件限制,公司必须在4天内将这批鲜奶全部销售或加工完毕。
(1)请你为此公司研制三种可行方案;
(1)你认为选择哪种方案获利最多?为什么?
探究新知
解:(1)
方案一:将鲜奶全部直接销售.
方案二:尽可能地对鲜奶制成奶片,没有来得及进行加工的鲜奶直接在市场销售.
方案三:将鲜奶部件制成奶片,其余鲜奶制成酸奶,并恰好4天完成.
(2)
方案一:获利为9 ×500=4500(元)
方案二:4天制成酸奶4 ×1=4(吨),还有5吨需要在市场直接销售,
获利为9 ×500=4500(元)
探究新知
方案三:设制成酸片x吨,制成酸奶(9-x)吨,根据题意,得
∴获利为1200 ×7.5+2000 × 2=12000(元)
答:选择方案三获利最多.
探究新知
例题小结
(1)弄清题意
(2)找准题中的等量关系.
(3)设出未知数.
(2)解出方程并答题.
1.小明和小红一起拼购购买相同的学习机,甲店承诺若一次购买两台学习机,其中台按原价而另一台可获得七折优惠,乙店承诺若一次购买两台学习机,按总价的80%收费,在哪家店购买学习更优惠( )
乙比甲优惠 B. 甲比乙优惠
C. 甲乙一样 D. 以上都有可能
A
课堂练习
课堂练习
2.甲乙两家手机店出售某型号定价相同的手机,甲店手机连续降价15%,乙店手机一次降价30%,在哪家手机店购买手机更合算( )
A.甲 B. 乙 C. 甲乙一样 D与价格有关
B
课堂练习
3.某公园的门票价格规定如下表:
购票人数 1—50人 51—100人 100人以上
每人门票价 25 23 21
公学校七年级(1)、 (2)两班共有104名学生去公园游玩,其中甲班的人数少于50人,乙班的人数多于50人,若两班都以班为单位分别购票,则共需付款2488元。问:
(1)两班各有多少个学生?
(2)怎样购票最为划算?
解:(1)设甲班有x个学生,则乙班有(104-x)个学生,根据题意得
13x +(104-x)=2488
解得x =48
所以104-x =56
答:甲班有48个学生,则乙班有56个学生.
(2)两班都以班为单位分别购票,则共需付款2488元。若两班作为一个团体购票:
104×21=2184(元)
2488-2184=304(元)
答:两班作为一个团体购票最为划算,可以省了304元
课堂练习
课堂练习
4.某市剧院举办大型文艺演出,其门票价格为:一等席300元/人,二等席200元/人,三等席150元/人,某公司组织36名员工去观看,计划用5850元购买2种门票,请你帮助公司设计可能的购票方案.
(1)设买一等席门票x张,则买二等席门票(36-x)张,根据题意,得
300x+200(36-x)=5 850,
解得x=-13.5,
票数不能为负数,不符题意,舍去.
(2)设买二等席门票y张,则买三等席门票(36-y)张.根据题意,得200y+150(36-y)=5 850,
解得y=9,所以36-9=27.
(3)设买一等席门票z张,则三等席门票(36-z)张.根据题意,得300z+150(36-z)=5 850,
解得z=3,所以36-3=33.
综上,共有两种方案:
买二等席门票9张,三等席门票27张或买一等席门票3张,三等席门票33张.
课堂练习
谈谈你们这节课有什么收获呢?
1策略问题
2电话计费问题
3方案设计问题
课堂小结
第106页
练习第2、3题
课外作业
https://www.21cnjy.com/help/help_extract.php
