1.3.2 函数的奇偶性1共17张PPT
文档属性
| 名称 | 1.3.2 函数的奇偶性1共17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 657.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
函数的奇偶性
x
y
o
x
y
o
观察下列两个函数图象并思考以下问题:
(1)这两个函数图象有什么共同特征吗?
(2)相应的两个函数值对应表是如何体现这些特征的?
x -3 -2 -1 0 1 2 3
x -3 -2 -1 0 1 2 3
我们得到,这两个函数图象都关于
y轴对称.从函数值对应表可以看到,
当自变量x取一对相反数时,相应的
两个函数值相同.即点(x,f(x))在图象
上,相应的点(-x,f(x))也在函数图象上。
我们能否利用函数解析式来描述函
数图象的特征呢?
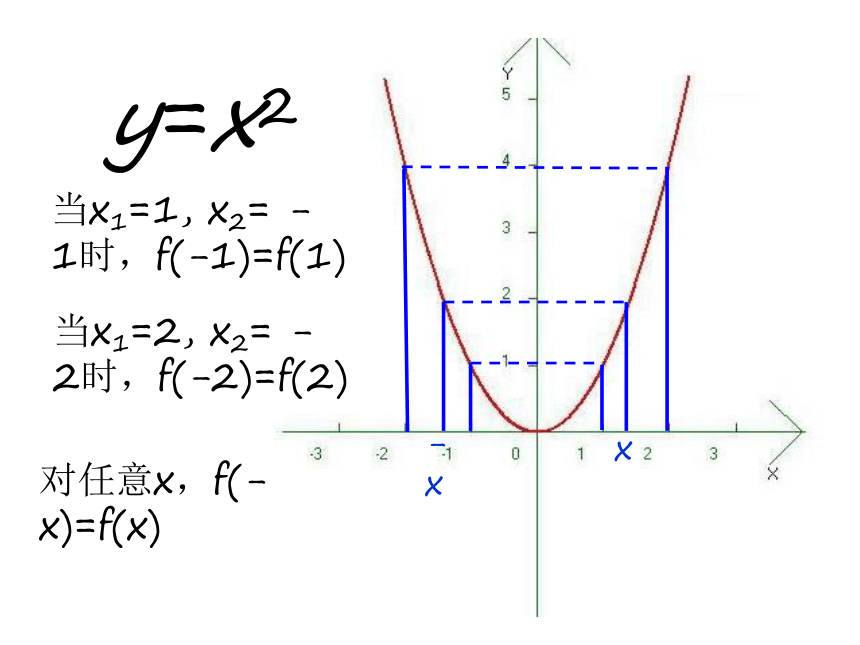
y=x2
-x
x
当x1=1, x2= -1时,f(-1)=f(1)
当x1=2, x2= -2时,f(-2)=f(2)
对任意x,f(-x)=f(x)
偶函数定义:如果对于函数定义域内的任意一个x ,都有f(-x)=f(x)。那么f(x)就叫偶函数。
奇函数定义:如果对于函数定义域内的任意一个x ,都有f(-x)=
-f(x)。那么f(x)就叫奇函数。
思考:偶函数与奇函数图象有什么
特征呢?
偶函数的图象关于
Y轴对称.
函数y=x2的图像
偶函数的图像特征
奇函数的图像特征
函数y=x3的图像
O
奇函数的图象关于原点对称.
例1.根据下列函数图象,判断函数奇偶性.
y
x
y
x
y
x
-1
2
y
x
-1
1
例1.判断下列函数的奇偶性:
解:(1)对于函数 ,其定义域为 ,因为对定义域内的每一个x,都有
所以函数 为奇函数。
(1)
(2)
先确定定义域,再验证f(x)与f(-x)之间的关系.
(3)
(2)对于函数 ,其定义域为
{x|x 0},定义域内每个x,都有
故f(x)为偶函数。
(3)f(x)定义域为R,定义域内每个x都有
故f(x)为奇函数.
(5)
(4)
定义域关于原 点对称是函数具有奇偶性的必要条件。
定义域不关于原点对称,所以
f(x)为非奇非偶函数。
解:(4)
变式:(1)若f(x)=2x呢?(2)f(x)=2x+ b呢?
(5)
,故函数f(x)为非奇非偶函数。
解:(1)f(x)=2x的定义域为R,其内
每个x,都有f(-x)=-f(x).
故f(x)为奇函数.
(2)f(x)=2x+b的定义域为R,
f(-x)=-2x+b,又f(x)=2x+b,
当b=0时,f(-x)=-f(x),故f(x)是奇函数;
当b 0时,f(-x) f(x),且f(-x) -f(x),
故f(x)是非奇非偶函数.
判断函数奇偶性步骤:
(1)先确定函数定义域,并判断
定义域是否关于原点对称;
(2)确定f(x)与f(-x)的关系;
(3)作出结论.
若f(-x)=f(x)或f(-x)-f(x)=0,
则f(x)是偶函数;
若f(-x)= - f(x)或f(-x)+f(x)=0,
则f(x)是奇函数.
思考:
(1)判断函数 的奇偶性.
(2)如果右图是函数
图象一部分,你能根据f(x)
的奇偶性画出它在y轴
左边的图象吗?
y
x
0
f(x)是奇函数.
其图象关于原点对称.
小结:
奇偶性定义:对于函数f(x),在它的定义域内,把任意一个x换成-x,(x,-x均在定义域内)
①若有f(-x)=-f(x), 则f(x)叫做奇函数;
②若有f(-x)=f(x), 则f(x)叫做偶函数。
定义域关于原点对称是函数具有奇偶性的必
要条件。
性质: 奇函数的图象关于原点对称;
偶函数的图象关于y轴对称.
判断奇偶性方法:图象法,定义法。
思考题:
判断下列函数奇偶性.
(1)f(x)=0;
(2)
(3)f(x)=
x(1-x),(x>0)
x(1+x),(x 0).
作业: 课本:
1 , 2
函数的奇偶性
x
y
o
x
y
o
观察下列两个函数图象并思考以下问题:
(1)这两个函数图象有什么共同特征吗?
(2)相应的两个函数值对应表是如何体现这些特征的?
x -3 -2 -1 0 1 2 3
x -3 -2 -1 0 1 2 3
我们得到,这两个函数图象都关于
y轴对称.从函数值对应表可以看到,
当自变量x取一对相反数时,相应的
两个函数值相同.即点(x,f(x))在图象
上,相应的点(-x,f(x))也在函数图象上。
我们能否利用函数解析式来描述函
数图象的特征呢?
y=x2
-x
x
当x1=1, x2= -1时,f(-1)=f(1)
当x1=2, x2= -2时,f(-2)=f(2)
对任意x,f(-x)=f(x)
偶函数定义:如果对于函数定义域内的任意一个x ,都有f(-x)=f(x)。那么f(x)就叫偶函数。
奇函数定义:如果对于函数定义域内的任意一个x ,都有f(-x)=
-f(x)。那么f(x)就叫奇函数。
思考:偶函数与奇函数图象有什么
特征呢?
偶函数的图象关于
Y轴对称.
函数y=x2的图像
偶函数的图像特征
奇函数的图像特征
函数y=x3的图像
O
奇函数的图象关于原点对称.
例1.根据下列函数图象,判断函数奇偶性.
y
x
y
x
y
x
-1
2
y
x
-1
1
例1.判断下列函数的奇偶性:
解:(1)对于函数 ,其定义域为 ,因为对定义域内的每一个x,都有
所以函数 为奇函数。
(1)
(2)
先确定定义域,再验证f(x)与f(-x)之间的关系.
(3)
(2)对于函数 ,其定义域为
{x|x 0},定义域内每个x,都有
故f(x)为偶函数。
(3)f(x)定义域为R,定义域内每个x都有
故f(x)为奇函数.
(5)
(4)
定义域关于原 点对称是函数具有奇偶性的必要条件。
定义域不关于原点对称,所以
f(x)为非奇非偶函数。
解:(4)
变式:(1)若f(x)=2x呢?(2)f(x)=2x+ b呢?
(5)
,故函数f(x)为非奇非偶函数。
解:(1)f(x)=2x的定义域为R,其内
每个x,都有f(-x)=-f(x).
故f(x)为奇函数.
(2)f(x)=2x+b的定义域为R,
f(-x)=-2x+b,又f(x)=2x+b,
当b=0时,f(-x)=-f(x),故f(x)是奇函数;
当b 0时,f(-x) f(x),且f(-x) -f(x),
故f(x)是非奇非偶函数.
判断函数奇偶性步骤:
(1)先确定函数定义域,并判断
定义域是否关于原点对称;
(2)确定f(x)与f(-x)的关系;
(3)作出结论.
若f(-x)=f(x)或f(-x)-f(x)=0,
则f(x)是偶函数;
若f(-x)= - f(x)或f(-x)+f(x)=0,
则f(x)是奇函数.
思考:
(1)判断函数 的奇偶性.
(2)如果右图是函数
图象一部分,你能根据f(x)
的奇偶性画出它在y轴
左边的图象吗?
y
x
0
f(x)是奇函数.
其图象关于原点对称.
小结:
奇偶性定义:对于函数f(x),在它的定义域内,把任意一个x换成-x,(x,-x均在定义域内)
①若有f(-x)=-f(x), 则f(x)叫做奇函数;
②若有f(-x)=f(x), 则f(x)叫做偶函数。
定义域关于原点对称是函数具有奇偶性的必
要条件。
性质: 奇函数的图象关于原点对称;
偶函数的图象关于y轴对称.
判断奇偶性方法:图象法,定义法。
思考题:
判断下列函数奇偶性.
(1)f(x)=0;
(2)
(3)f(x)=
x(1-x),(x>0)
x(1+x),(x 0).
作业: 课本:
1 , 2
