1.3.5二次函数性质的再研究 课件(27张PPT)
文档属性
| 名称 | 1.3.5二次函数性质的再研究 课件(27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 694.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览



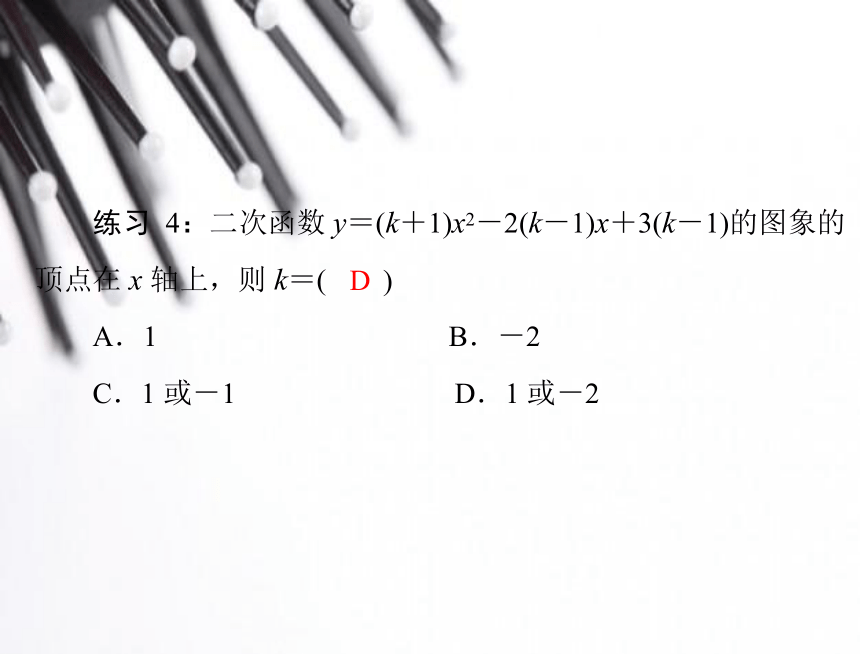



文档简介
(共27张PPT)
1.3.5
二次函数性质的再研究
【学习目标】
1.理解二次函数的图象特征及其解析式.
2.探讨二次函数的性质.
二次函数的系数
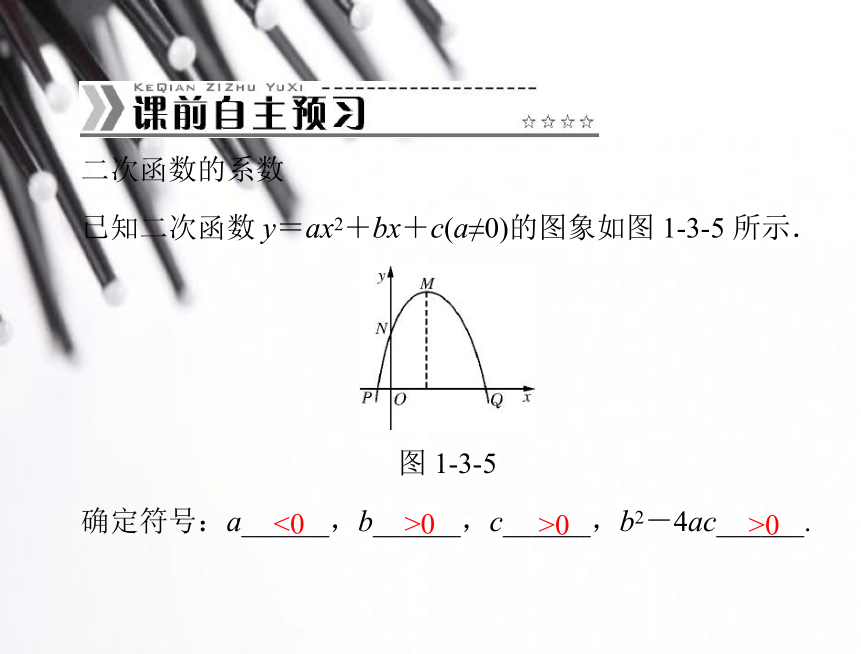
已知二次函数 y=ax2+bx+c(a≠0)的图象如图 1-3-5 所示.
图 1-3-5
确定符号:a______,b______,c______,b2-4ac______.
<0
>0
>0
>0
练习 1:若 y=x2+ax+b 在[0,1]上的最大值为 1,最小值为
0,且 a≤-2,则 a=________,b=________.
-2
1
最小值为________.
-8
x=-2
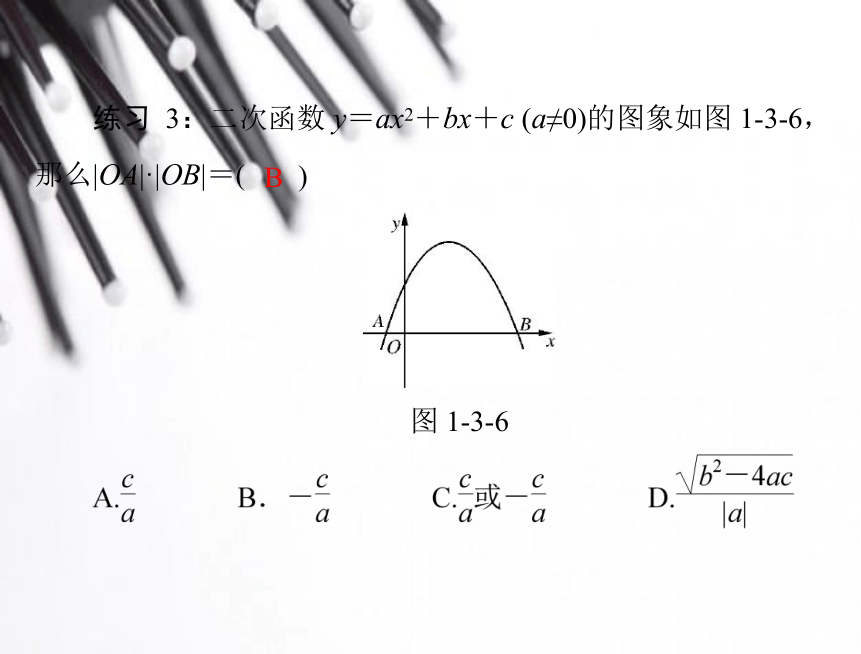
练习 3:二次函数 y=ax2+bx+c (a≠0)的图象如图 1-3-6,
那么|OA|·|OB|=(
)
图 1-3-6
B
练习 4:二次函数 y=(k+1)x2-2(k-1)x+3(k-1)的图象的
)
顶点在 x 轴上,则 k=(
A.1
C.1 或-1
B.-2
D.1 或-2
D
【问题探究】
1.二次函数 f(x)=ax2+bx+c 在什么情况下是偶函数?可
以是奇函数吗?
答案:当 b=0 时为偶函数;不可能是奇函数.
2.二次函数 f(x)=ax2+bx+c 的单调性是由哪些要素来确
定的?试写出其单调区间.
答案:二次函数 f(x)=ax2+bx+c 的单调性由开口方向和对
称轴确定的.
题型 1
求二次函数的值域
【例 1】 根据函数单调性求出下列函数的值域:
(1)f(x)=x2+4x-1,x∈[-4,-3];
(2)f(x)=-2x2-x+4,x∈[-3,-1];
(3)f(x)=2x2-4x-1,x∈(-1,3);
解:(1)f(x)=x2+4x-1=(x+2)2-5,
在[-4,-3]上单调递减,y∈[-4,-1].
在 x∈[-3,-1]上单调递增,y∈[-11,3].
(3)f(x)=2x2-4x-1=2(x-1)2-3,
x∈(-1,3),当 x=1 时,取得最小值为-3,
又∵f(-1)=5,f(3)=5,∴y∈[-3,5).
求二次函数在某个区间的最值,最容易出现的
错误是直接代两头(将两端点代入),当然这样做,有时答案也
对,那是因为在该区间函数刚好单调,这纯属巧合.求二次函
数在某个区间的最值时,应先配方,找到对称轴和顶点,再结
合图形进行求解.
【变式与拓展】
解:二次函数 y=3-2x-x2 的对称轴为
画出函数的图象,由图 D21,可知:当 x
=-1 时,ymax=4.
图D21
题型 2
轴定区间动问题的分类讨论
【例 2】 设函数 f(x)=x2-2x-2(其中 x∈[t,t+1],t∈R)
的最小值为 g(t),求 g(t)的表达式.
解:f(x)=x2-2x-2=(x-1)2-3,
当 t+1≤1,即 t≤0 时,由图 D14 可知:截取减区间上的
一段,g(t)=f(t+1)=t2-3.
图 D14
当 1
D15,g(t)=f(1)=-3.
当 t+1>2,即 t>1 时,截取增区间上的一段,如图 D16,
g(t)=f(t)=t2-2t-2.
图 D15
图 D16
这是一道与二次函数有关的含参数的问题,本
例的二次函数的对称轴固定,而区间不固定,因此需要讨论该
区间相对于对称轴的位置关系.
【变式与拓展】
2.二次函数 y=-2x2+x+1,定义域为[t,t+1](t 为可变
常数),下列命题中错误的是(
)
A
题型 3 区间定轴动问题的分类讨论
【例 3】 求函数 f(x)=x2-2ax-1 在区间[0,2]上的最大值
和最小值.
解:∵f(x)=x2-2ax-1=(x-a)2-a2-1.
∴f(x)的图象是开口向上,对称轴为 x=a 的抛物线.
当 a<0 时(如图 D17),f(x)的最大值为 f(2)=3-4a,f(x)的
最小值为 f(0)=-1.
图 D17
当 0≤a≤1 时(如图D18),f(x)的最大值为 f(2)=3-4a,f(x)
的最小值为 f(a)=-a2-1.
图 D18
图 D19
当 1
最小值为 f(a)=-a2-1.
当 a≥2 时(如图 D20),f(x)的最大值为 f(0)=-1,f(x)的最
小值为 f(2)=3-4a.
图 D20
本例是与二次函数有关的含参数的问题,本例
的二次函数是区间固定,对称轴变化,因此要讨论对称轴相对
于该区间的位置关系,例 2 和例 3 是二次函数中分类讨论中的
最基本的两种题型,应引起足够的重视.
【变式与拓展】
3.已知函数 f(x)=-x2+kx 在[1,3]上是单调函数,则实数
k 的取值范围为____________.
k≤2 或 k≥6
【例 4】 已知函数 f(x)=x2+ax+3-a,若当 x∈[-2,2]时,
f(x)≥0 恒成立,求实数 a 的取值范围.
易错分析:对二次函数 f(x)=ax2+bx+c(a>0),当 x∈R,
f(x)≥0 恒成立时,有Δ≤0.
片面理解为当 ax2+bx+c≥0(a>0),x∈[-2,2]恒成立时,
这都是由于函数性质掌握得不透彻而导致的错误.在二次
函数最值问题中,“轴变区间定问题”要对对称轴进行分类讨
论,“轴定区间变问题”要对区间进行分类讨论.
解:设 f(x)的最小值为 g(a).
又 a<-4,故-7≤a<-4.
综上所述,实数 a 的取值范围为-7≤a≤2.
[方法·规律·小结]
1.二次函数的解析式有三种形式.
(1)一般式:f(x)=ax2+bx+c(a≠0).
(2)顶点式:f(x)=a(x-m)2+n (a≠0),其中,顶点为(m,n).
(3)两根式 f(x)=a(x-x1)(x-x2)(a≠0),x1,x2 为二次函数的
图象与 x 轴的两个交点的横坐标.
3.二次函数的单调性只与对称轴和开口方向有关,因此,
其单调性的判断通常用数形结合法.
4.与二次函数有关的不等式恒成立问题要注意二次项系数
为零的特殊情形.
1.3.5
二次函数性质的再研究
【学习目标】
1.理解二次函数的图象特征及其解析式.
2.探讨二次函数的性质.
二次函数的系数
已知二次函数 y=ax2+bx+c(a≠0)的图象如图 1-3-5 所示.
图 1-3-5
确定符号:a______,b______,c______,b2-4ac______.
<0
>0
>0
>0
练习 1:若 y=x2+ax+b 在[0,1]上的最大值为 1,最小值为
0,且 a≤-2,则 a=________,b=________.
-2
1
最小值为________.
-8
x=-2
练习 3:二次函数 y=ax2+bx+c (a≠0)的图象如图 1-3-6,
那么|OA|·|OB|=(
)
图 1-3-6
B
练习 4:二次函数 y=(k+1)x2-2(k-1)x+3(k-1)的图象的
)
顶点在 x 轴上,则 k=(
A.1
C.1 或-1
B.-2
D.1 或-2
D
【问题探究】
1.二次函数 f(x)=ax2+bx+c 在什么情况下是偶函数?可
以是奇函数吗?
答案:当 b=0 时为偶函数;不可能是奇函数.
2.二次函数 f(x)=ax2+bx+c 的单调性是由哪些要素来确
定的?试写出其单调区间.
答案:二次函数 f(x)=ax2+bx+c 的单调性由开口方向和对
称轴确定的.
题型 1
求二次函数的值域
【例 1】 根据函数单调性求出下列函数的值域:
(1)f(x)=x2+4x-1,x∈[-4,-3];
(2)f(x)=-2x2-x+4,x∈[-3,-1];
(3)f(x)=2x2-4x-1,x∈(-1,3);
解:(1)f(x)=x2+4x-1=(x+2)2-5,
在[-4,-3]上单调递减,y∈[-4,-1].
在 x∈[-3,-1]上单调递增,y∈[-11,3].
(3)f(x)=2x2-4x-1=2(x-1)2-3,
x∈(-1,3),当 x=1 时,取得最小值为-3,
又∵f(-1)=5,f(3)=5,∴y∈[-3,5).
求二次函数在某个区间的最值,最容易出现的
错误是直接代两头(将两端点代入),当然这样做,有时答案也
对,那是因为在该区间函数刚好单调,这纯属巧合.求二次函
数在某个区间的最值时,应先配方,找到对称轴和顶点,再结
合图形进行求解.
【变式与拓展】
解:二次函数 y=3-2x-x2 的对称轴为
画出函数的图象,由图 D21,可知:当 x
=-1 时,ymax=4.
图D21
题型 2
轴定区间动问题的分类讨论
【例 2】 设函数 f(x)=x2-2x-2(其中 x∈[t,t+1],t∈R)
的最小值为 g(t),求 g(t)的表达式.
解:f(x)=x2-2x-2=(x-1)2-3,
当 t+1≤1,即 t≤0 时,由图 D14 可知:截取减区间上的
一段,g(t)=f(t+1)=t2-3.
图 D14
当 1
D15,g(t)=f(1)=-3.
当 t+1>2,即 t>1 时,截取增区间上的一段,如图 D16,
g(t)=f(t)=t2-2t-2.
图 D15
图 D16
这是一道与二次函数有关的含参数的问题,本
例的二次函数的对称轴固定,而区间不固定,因此需要讨论该
区间相对于对称轴的位置关系.
【变式与拓展】
2.二次函数 y=-2x2+x+1,定义域为[t,t+1](t 为可变
常数),下列命题中错误的是(
)
A
题型 3 区间定轴动问题的分类讨论
【例 3】 求函数 f(x)=x2-2ax-1 在区间[0,2]上的最大值
和最小值.
解:∵f(x)=x2-2ax-1=(x-a)2-a2-1.
∴f(x)的图象是开口向上,对称轴为 x=a 的抛物线.
当 a<0 时(如图 D17),f(x)的最大值为 f(2)=3-4a,f(x)的
最小值为 f(0)=-1.
图 D17
当 0≤a≤1 时(如图D18),f(x)的最大值为 f(2)=3-4a,f(x)
的最小值为 f(a)=-a2-1.
图 D18
图 D19
当 1
最小值为 f(a)=-a2-1.
当 a≥2 时(如图 D20),f(x)的最大值为 f(0)=-1,f(x)的最
小值为 f(2)=3-4a.
图 D20
本例是与二次函数有关的含参数的问题,本例
的二次函数是区间固定,对称轴变化,因此要讨论对称轴相对
于该区间的位置关系,例 2 和例 3 是二次函数中分类讨论中的
最基本的两种题型,应引起足够的重视.
【变式与拓展】
3.已知函数 f(x)=-x2+kx 在[1,3]上是单调函数,则实数
k 的取值范围为____________.
k≤2 或 k≥6
【例 4】 已知函数 f(x)=x2+ax+3-a,若当 x∈[-2,2]时,
f(x)≥0 恒成立,求实数 a 的取值范围.
易错分析:对二次函数 f(x)=ax2+bx+c(a>0),当 x∈R,
f(x)≥0 恒成立时,有Δ≤0.
片面理解为当 ax2+bx+c≥0(a>0),x∈[-2,2]恒成立时,
这都是由于函数性质掌握得不透彻而导致的错误.在二次
函数最值问题中,“轴变区间定问题”要对对称轴进行分类讨
论,“轴定区间变问题”要对区间进行分类讨论.
解:设 f(x)的最小值为 g(a).
又 a<-4,故-7≤a<-4.
综上所述,实数 a 的取值范围为-7≤a≤2.
[方法·规律·小结]
1.二次函数的解析式有三种形式.
(1)一般式:f(x)=ax2+bx+c(a≠0).
(2)顶点式:f(x)=a(x-m)2+n (a≠0),其中,顶点为(m,n).
(3)两根式 f(x)=a(x-x1)(x-x2)(a≠0),x1,x2 为二次函数的
图象与 x 轴的两个交点的横坐标.
3.二次函数的单调性只与对称轴和开口方向有关,因此,
其单调性的判断通常用数形结合法.
4.与二次函数有关的不等式恒成立问题要注意二次项系数
为零的特殊情形.
