2.1.3-2.1.4 空间中直线与平面、平面与平面的位置关系2课件 新人教A版(共58张PPT)
文档属性
| 名称 | 2.1.3-2.1.4 空间中直线与平面、平面与平面的位置关系2课件 新人教A版(共58张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览







文档简介
(共58张PPT)
2.1.3空间中直线与平面之间的位置关系
2.1.4平面与平面之间的位置关系
直
线
和
平
面
直
线
和
平
面
例1 下列命题中,正确的个数是( )
①如果两条平行直线中的一条和一个平面相交,那么另一条直线也和这个平面相交;②一条直线和另一条直线平行,它就和经过另一条直线的任何平面都平行;③经过两条异面直线中的一条直线,有一个平面与另一条直线平行;④两条相交直线,其中一条与一个平面平行,则另一条一定与这个平面平行.
A.0 B.1
C.2 D.3
【分析】 本题主要考查直线与平面的位置关系,解答本题要牢牢地抓住直线和平面三种位置关系的特征,结合相关图形,依据位置关系的定义作出判断.
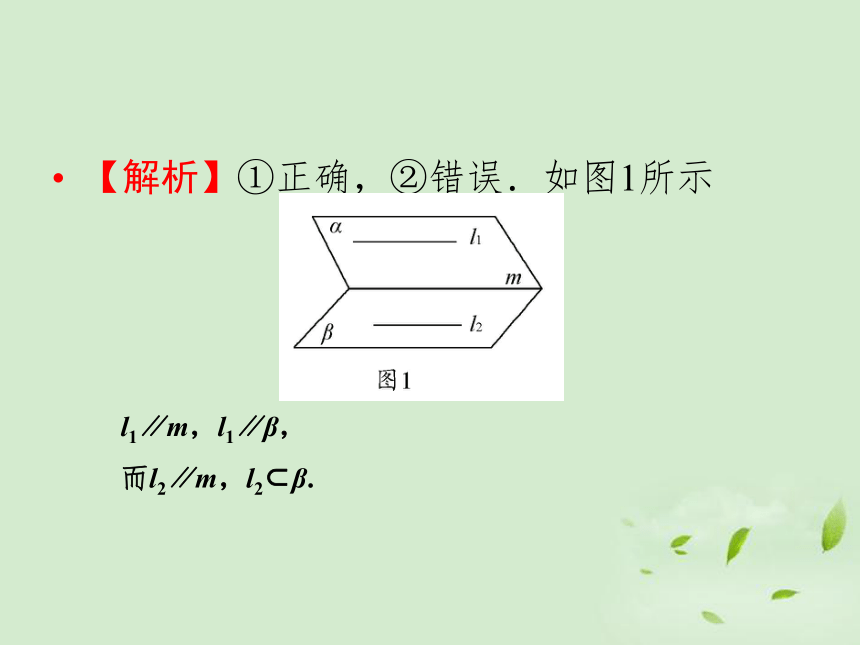
【解析】①正确,②错误.如图1所示
l1∥m,l1∥β,
而l2∥m,l2?β.
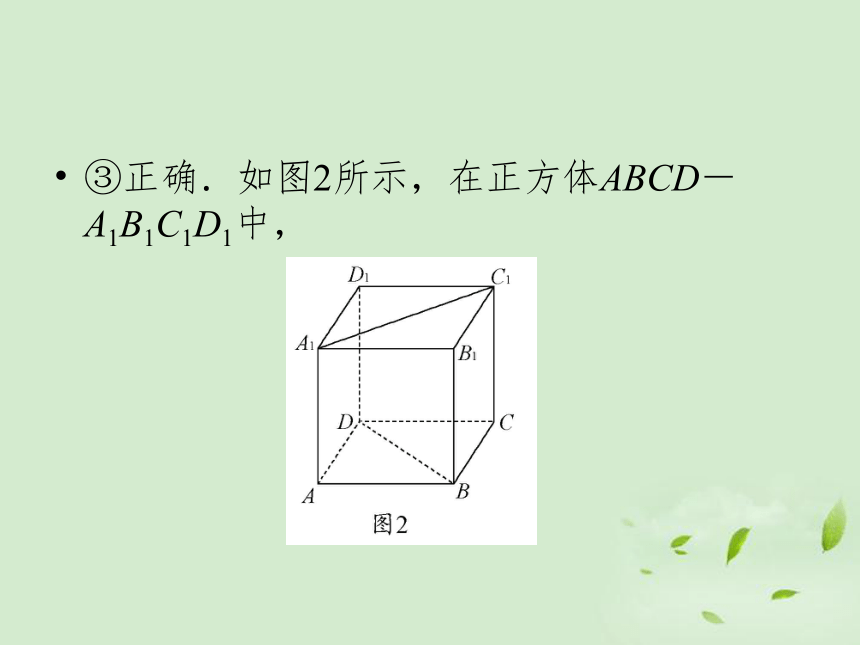
③正确.如图2所示,在正方体ABCD-A1B1C1D1中,
直线A1C1与直线BD异面,
A1C1?平面A1B1C1D1,且BD∥平面A1B1C1D1,
故③正确.
④错误,直线还可能与平面相交,由此可知,①③正确,故选C.
【答案】 C
【规律方法】 解答此类问题,首先要正确理解直线与平面的三种位置关系的定义:(1)在直线和平面的三种位置关系中,否定其中一种,其反面是另外两种位置关系;(2)直线和平面相交的定义中,“有且只有”包含两层含义:一是“有”表示存在;二是“只有”表示惟一.
变式1 (2010年四川模拟)对于不重合的两个平面α与β,给定下列条件:
①存在平面γ,使得α、β都平行于平面γ;
②α内有不共线的三点到平面β的距离相等;
③存在异面直线l、m,使得l∥α,l∥β,m∥α,m∥β.
其中可以判断两个平面α与β平行的条件有________.
解析:若α与β相交,如图,可在α内找到A、B、C三个点到平面β的距离相等,所以排除②.容易证明①③都是正确的.
答案:①③
要点二 平面与平面的位置关系
空间中的两个平面有且只有两种位置关系:两平面平行和两平面相交.
1.画两个平行平面时,要注意把表示平面的平等四边形画成对应边平行,如图.
2.画两个相交平面时,要注意画出交线,被遮挡住的部分用虚线或者不画.
例2 α、β是两个不重合的平面,下面说法中正确的是( )
A.平面α内有两条直线a、b都与平面β平行,那么α∥β
B.平面α内有无数条直线平行于平面β,那么α∥β
C.若直线a与平面α和平面β都成相等的角,那么α∥β
D.平面α内所有的直线都与平面β平行,那么α∥β
【分析】 解答本题要牢牢抓住平面平行的概念,即分析两平面是否可能有公共点,借助于图形更可事半功倍.
【解析】 根据两平面相交和平行的定义,结合图形判断如下图所示.A、B都不能保证α、β无公共点,如图1;C中当a∥α,a∥β且α与β相交时,a与α、β也成等角,但α与β不平行,如图2;所在只有D说明α、β一定无公共点.
【答案】 D
【规律方法】 判断两平面的位置关系,通常是结合条件,综合考虑各种因素并借助图形,同时要区别无数与任意的不同.
变式2 已知平面α∥平面β,l?α,则( )
A.l?β B.l∥β
C.l,β相交 D.以上均有可能
解析:如图所示.
由于平面α∥平面β,所以平面α,β无公共点,又l?α,所以l,β无公共点.所以l∥β.
答案:B
要点三 线线、线面、面面位置关系综合研究
要判断线线、线面、面面位置关系时,除清楚定义外,还要利用好身边的模型,尤其是“长方形”这个模型。
例3 已知a、b、c为三条不重合的直线,α、β为两个不重合的平面.
①a∥c,b∥c?a∥b;②a∥β,b∥β?a∥b;
③a∥c,c∥α?a∥α;④a∥β,a∥α?α∥β;
⑤a?α,b?α,a∥b?a∥α.
其中正确的命题是( )
A.①⑤ B.①②
C.②④ D.③⑤
【分析】 本题主要考查直线与直线、直线与平面、平面与平面的位置关系.解答本题要考虑线线、线面、面面位置关系的特征与定义,结合空间想象能力作出判断.
【解析】 由公理4知①正确;由直线与平面平行的位置关系知⑤正确.从而选A.其中②是错误的,因为平行于同一平面的两条直线可能平行、可能相交,也可能异面.③是错误的,因为当a∥c,c∥α时,可能a∥α,也可能a?α.对于④,α,β可能平行,也可能相交.
【答案】 A
【规律方法】 判断线线、线面、面面的位置关系,要牢牢地抓住其特征与定义,要有画图的意识,结合空间想象能力全方位、多角度地去考虑问题,作出判断.
变式3 给出下列几个命题:
①过一点有且只有一条直线与已知直线平行;
②过一点有且只有一条直线与已知直线垂直;
③过平面外一点有且只有一条直线与该平面平行;
④过平面外一点有且只有一个平面与该平面平行.
其中正确命题的个数为( )
A.0 B.1
C.2 D.3
解析:①当点在已知直线上时,不存在过该点的直线与该直线平行,故①错;
②由于垂直包括相交垂直和异面垂直,因而过一点与一条已知直线垂直的直线有无数条,故②错;
③过平面外一点与已知平面平行的直线有无数条,故③错;
④过平面外一点与已知平面平行的平面有且只有一个,故④对.
答案:B
2.1.3空间中直线与平面之间的位置关系
2.1.4平面与平面之间的位置关系
直
线
和
平
面
直
线
和
平
面
例1 下列命题中,正确的个数是( )
①如果两条平行直线中的一条和一个平面相交,那么另一条直线也和这个平面相交;②一条直线和另一条直线平行,它就和经过另一条直线的任何平面都平行;③经过两条异面直线中的一条直线,有一个平面与另一条直线平行;④两条相交直线,其中一条与一个平面平行,则另一条一定与这个平面平行.
A.0 B.1
C.2 D.3
【分析】 本题主要考查直线与平面的位置关系,解答本题要牢牢地抓住直线和平面三种位置关系的特征,结合相关图形,依据位置关系的定义作出判断.
【解析】①正确,②错误.如图1所示
l1∥m,l1∥β,
而l2∥m,l2?β.
③正确.如图2所示,在正方体ABCD-A1B1C1D1中,
直线A1C1与直线BD异面,
A1C1?平面A1B1C1D1,且BD∥平面A1B1C1D1,
故③正确.
④错误,直线还可能与平面相交,由此可知,①③正确,故选C.
【答案】 C
【规律方法】 解答此类问题,首先要正确理解直线与平面的三种位置关系的定义:(1)在直线和平面的三种位置关系中,否定其中一种,其反面是另外两种位置关系;(2)直线和平面相交的定义中,“有且只有”包含两层含义:一是“有”表示存在;二是“只有”表示惟一.
变式1 (2010年四川模拟)对于不重合的两个平面α与β,给定下列条件:
①存在平面γ,使得α、β都平行于平面γ;
②α内有不共线的三点到平面β的距离相等;
③存在异面直线l、m,使得l∥α,l∥β,m∥α,m∥β.
其中可以判断两个平面α与β平行的条件有________.
解析:若α与β相交,如图,可在α内找到A、B、C三个点到平面β的距离相等,所以排除②.容易证明①③都是正确的.
答案:①③
要点二 平面与平面的位置关系
空间中的两个平面有且只有两种位置关系:两平面平行和两平面相交.
1.画两个平行平面时,要注意把表示平面的平等四边形画成对应边平行,如图.
2.画两个相交平面时,要注意画出交线,被遮挡住的部分用虚线或者不画.
例2 α、β是两个不重合的平面,下面说法中正确的是( )
A.平面α内有两条直线a、b都与平面β平行,那么α∥β
B.平面α内有无数条直线平行于平面β,那么α∥β
C.若直线a与平面α和平面β都成相等的角,那么α∥β
D.平面α内所有的直线都与平面β平行,那么α∥β
【分析】 解答本题要牢牢抓住平面平行的概念,即分析两平面是否可能有公共点,借助于图形更可事半功倍.
【解析】 根据两平面相交和平行的定义,结合图形判断如下图所示.A、B都不能保证α、β无公共点,如图1;C中当a∥α,a∥β且α与β相交时,a与α、β也成等角,但α与β不平行,如图2;所在只有D说明α、β一定无公共点.
【答案】 D
【规律方法】 判断两平面的位置关系,通常是结合条件,综合考虑各种因素并借助图形,同时要区别无数与任意的不同.
变式2 已知平面α∥平面β,l?α,则( )
A.l?β B.l∥β
C.l,β相交 D.以上均有可能
解析:如图所示.
由于平面α∥平面β,所以平面α,β无公共点,又l?α,所以l,β无公共点.所以l∥β.
答案:B
要点三 线线、线面、面面位置关系综合研究
要判断线线、线面、面面位置关系时,除清楚定义外,还要利用好身边的模型,尤其是“长方形”这个模型。
例3 已知a、b、c为三条不重合的直线,α、β为两个不重合的平面.
①a∥c,b∥c?a∥b;②a∥β,b∥β?a∥b;
③a∥c,c∥α?a∥α;④a∥β,a∥α?α∥β;
⑤a?α,b?α,a∥b?a∥α.
其中正确的命题是( )
A.①⑤ B.①②
C.②④ D.③⑤
【分析】 本题主要考查直线与直线、直线与平面、平面与平面的位置关系.解答本题要考虑线线、线面、面面位置关系的特征与定义,结合空间想象能力作出判断.
【解析】 由公理4知①正确;由直线与平面平行的位置关系知⑤正确.从而选A.其中②是错误的,因为平行于同一平面的两条直线可能平行、可能相交,也可能异面.③是错误的,因为当a∥c,c∥α时,可能a∥α,也可能a?α.对于④,α,β可能平行,也可能相交.
【答案】 A
【规律方法】 判断线线、线面、面面的位置关系,要牢牢地抓住其特征与定义,要有画图的意识,结合空间想象能力全方位、多角度地去考虑问题,作出判断.
变式3 给出下列几个命题:
①过一点有且只有一条直线与已知直线平行;
②过一点有且只有一条直线与已知直线垂直;
③过平面外一点有且只有一条直线与该平面平行;
④过平面外一点有且只有一个平面与该平面平行.
其中正确命题的个数为( )
A.0 B.1
C.2 D.3
解析:①当点在已知直线上时,不存在过该点的直线与该直线平行,故①错;
②由于垂直包括相交垂直和异面垂直,因而过一点与一条已知直线垂直的直线有无数条,故②错;
③过平面外一点与已知平面平行的直线有无数条,故③错;
④过平面外一点与已知平面平行的平面有且只有一个,故④对.
答案:B
