2.2.2平面与平面平行的判定课件 公开课课件 新人教A版必修2共17张PPT
文档属性
| 名称 | 2.2.2平面与平面平行的判定课件 公开课课件 新人教A版必修2共17张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 731.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 22:40:53 | ||
图片预览

文档简介
(共17张PPT)
2.2.2平面与平面平行的判定
高一数学备课组
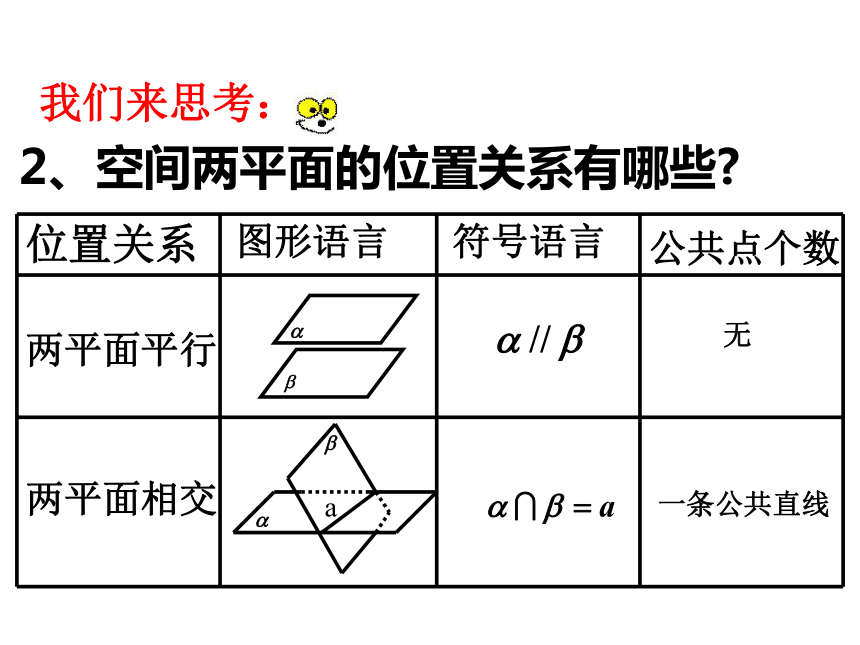
2、空间两平面的位置关系有哪些?
我们来思考:
无
一条公共直线
位置关系
两平面平行
两平面相交
公共点个数
图形语言
符号语言
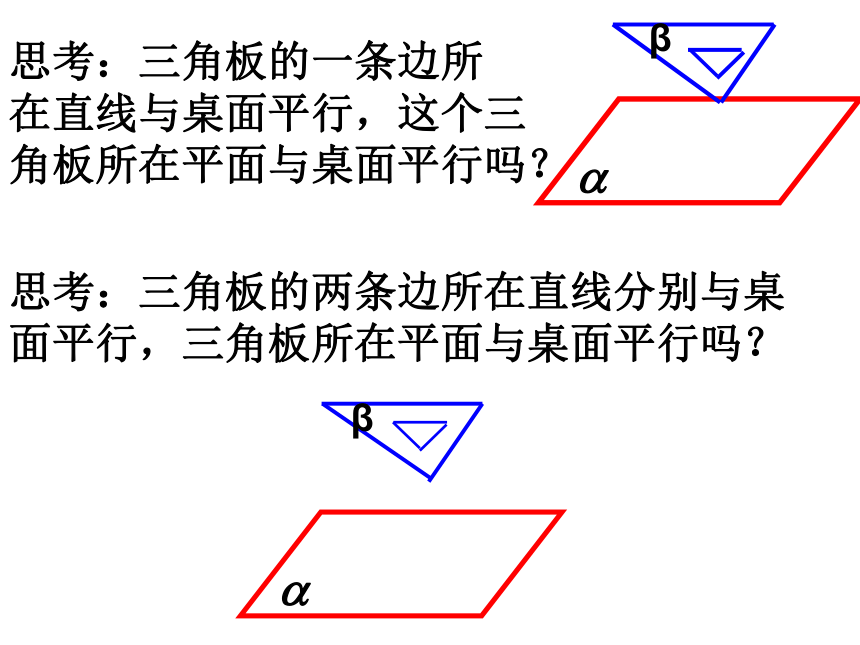
思考:三角板的两条边所在直线分别与桌
面平行,三角板所在平面与桌面平行吗?
思考:三角板的一条边所
在直线与桌面平行,这个三
角板所在平面与桌面平行吗?
β
β
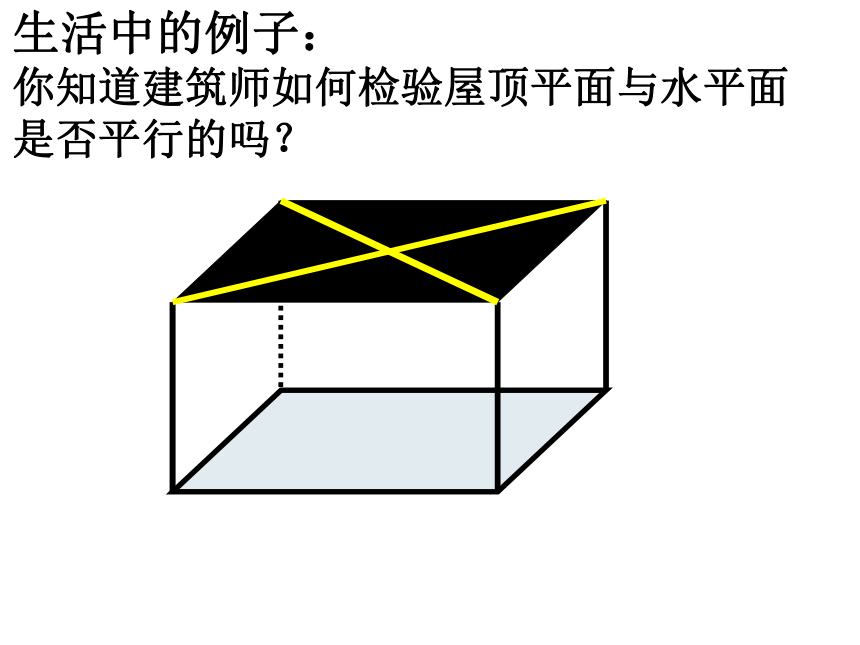
生活中的例子:
你知道建筑师如何检验屋顶平面与水平面
是否平行的吗?
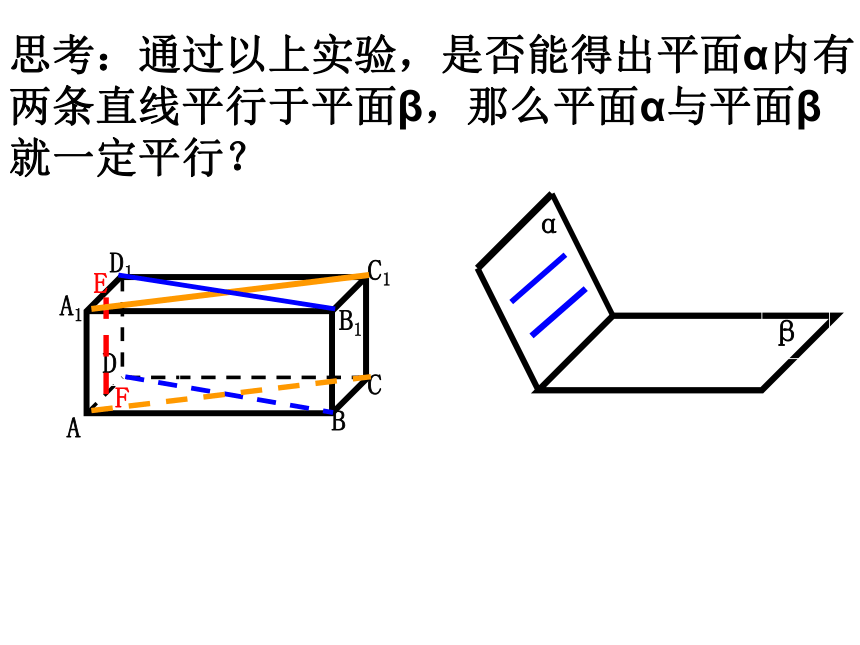
思考:通过以上实验,是否能得出平面α内有
两条直线平行于平面β,那么平面α与平面β
就一定平行?
p
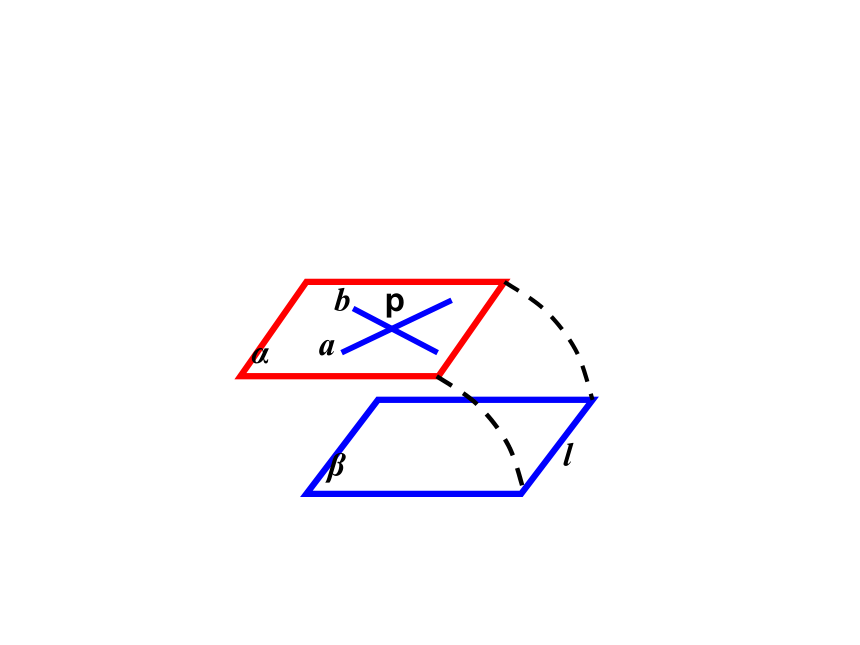
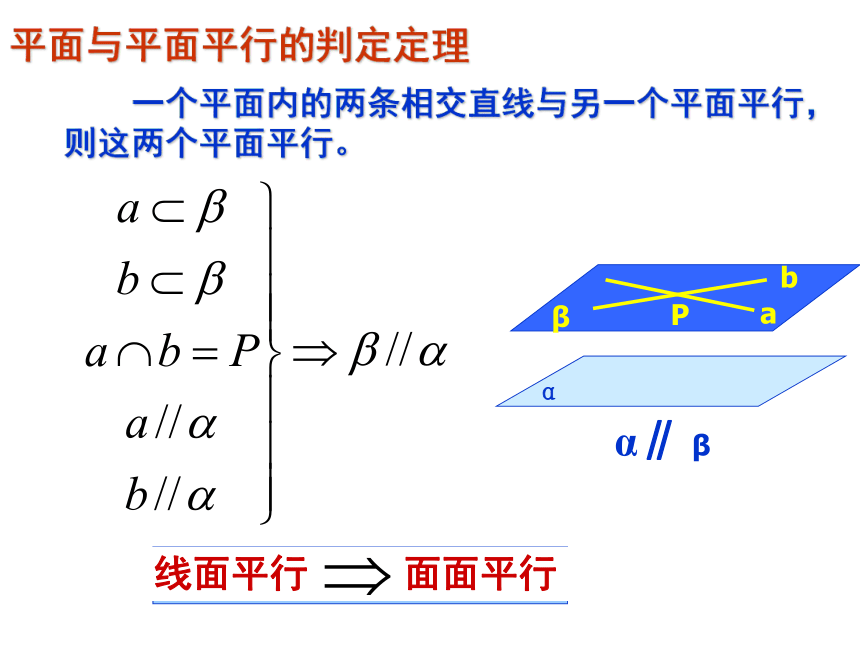
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.
推论:
p
p
p
p
基础尝试性练习
判断下列命题是否正确:
( )1、如果一个平面内有两条直线平行于另一个
平面,那么这两个平面平行;
( ) 2、如果一个平面内有两条不平行的直线都平
行于另一个平面,那么这两个平面平行;
( )3、如果一个平面内有无数条直线分别平行于
另一个平面,那么这两个平面平行;
( )4、如果一个平面内任意一条直线都平行于另
一个平面,那么这两个平面平行.
理论迁移
例1 在正方体ABCD-A′B′C′D′中. 求证:平面AB′D′∥平面BC′D.
已知正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,
求证:平面AMN∥平面EFDB
定理应用
能力训练
∴MN∥B1D1 B1D1∥EF
∴MN∥EF
MN∥平面BDFE
MF∥A1D1, A1D1∥AD∴
MF∥AD
且MF=A1D1
= AD
AM ∥DF
∴ AM∥平面DBEF
∴平面AMN∥平面EFDB
拓展探究
如图,ABCD和ABEF均为正方形,M、N分别是对角线AC、BF上的一点,且AM=FN,如果过MN作一平面平行于平面BCE,应该怎样画线?
定理应用
G
M
N
新知识总结
通过这节课的学习,你觉得掌握了哪些知识和方法?有哪些体会?
平面和平面平行的判定方法:
(A组)P62 习题2.2 A组 第7题;
(B组)如右图,B为△ADC所在平面外一点,
M、N、G分别为△ABC、△ABD、△BCD的重心,
求证:平面GMN∥平面ACD.
作业
以下两组中任选一组做作业:
例2 在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,求证:
平面DEF//平面ABC.
2.2.2平面与平面平行的判定
高一数学备课组
2、空间两平面的位置关系有哪些?
我们来思考:
无
一条公共直线
位置关系
两平面平行
两平面相交
公共点个数
图形语言
符号语言
思考:三角板的两条边所在直线分别与桌
面平行,三角板所在平面与桌面平行吗?
思考:三角板的一条边所
在直线与桌面平行,这个三
角板所在平面与桌面平行吗?
β
β
生活中的例子:
你知道建筑师如何检验屋顶平面与水平面
是否平行的吗?
思考:通过以上实验,是否能得出平面α内有
两条直线平行于平面β,那么平面α与平面β
就一定平行?
p
平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.
推论:
p
p
p
p
基础尝试性练习
判断下列命题是否正确:
( )1、如果一个平面内有两条直线平行于另一个
平面,那么这两个平面平行;
( ) 2、如果一个平面内有两条不平行的直线都平
行于另一个平面,那么这两个平面平行;
( )3、如果一个平面内有无数条直线分别平行于
另一个平面,那么这两个平面平行;
( )4、如果一个平面内任意一条直线都平行于另
一个平面,那么这两个平面平行.
理论迁移
例1 在正方体ABCD-A′B′C′D′中. 求证:平面AB′D′∥平面BC′D.
已知正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点,
求证:平面AMN∥平面EFDB
定理应用
能力训练
∴MN∥B1D1 B1D1∥EF
∴MN∥EF
MN∥平面BDFE
MF∥A1D1, A1D1∥AD∴
MF∥AD
且MF=A1D1
= AD
AM ∥DF
∴ AM∥平面DBEF
∴平面AMN∥平面EFDB
拓展探究
如图,ABCD和ABEF均为正方形,M、N分别是对角线AC、BF上的一点,且AM=FN,如果过MN作一平面平行于平面BCE,应该怎样画线?
定理应用
G
M
N
新知识总结
通过这节课的学习,你觉得掌握了哪些知识和方法?有哪些体会?
平面和平面平行的判定方法:
(A组)P62 习题2.2 A组 第7题;
(B组)如右图,B为△ADC所在平面外一点,
M、N、G分别为△ABC、△ABD、△BCD的重心,
求证:平面GMN∥平面ACD.
作业
以下两组中任选一组做作业:
例2 在三棱锥P-ABC中,点D、E、F分别是△PAB、△PBC、△PAC的重心,求证:
平面DEF//平面ABC.
