人教B版数学必修4 1.1.2 弧度制和弧度制与角度制的换算(共17张ppt)
文档属性
| 名称 | 人教B版数学必修4 1.1.2 弧度制和弧度制与角度制的换算(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 210.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览



文档简介
课件17张PPT。姚明在篮球场上被称为中国移动的长城,在美国NBA 介绍姚明的身高是7英尺5英寸,在中国介绍他的身高为2.26米,这样看来姚明的身高可以用英尺和米来度量。姚明的身高是多少?思考:联系到我们现在学的必修四,角的度量除了用角度外,还有其它的度量方法么?1.1.2 弧度制和
弧度制与角度制的换算高中新课标人教B版必修4
1、理解弧度制的定义
2、熟练掌握角度与弧度之间的换算
3、熟练应用与扇形有关的公式
难点:对弧度制定义的理解
重点:熟练应用与扇形有关的公式
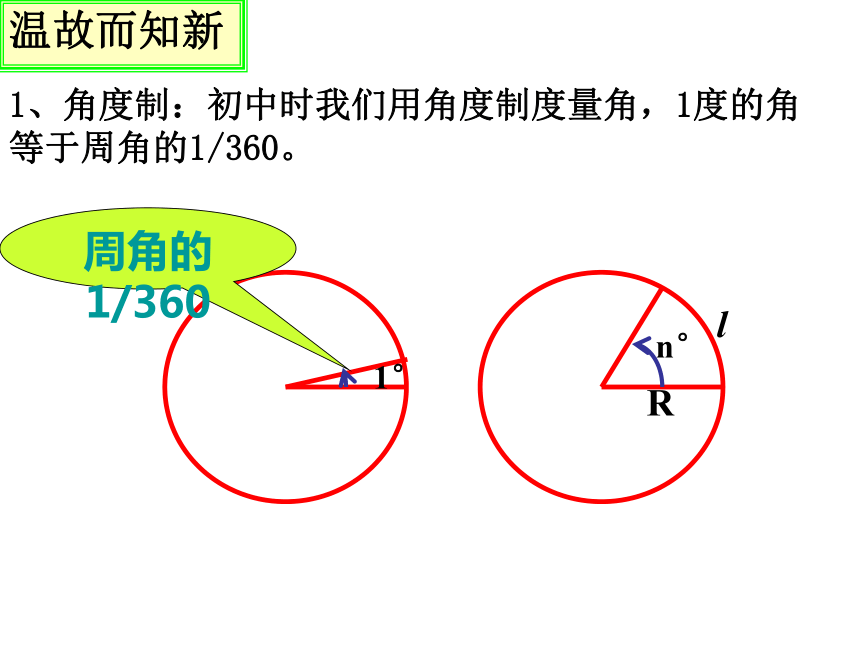
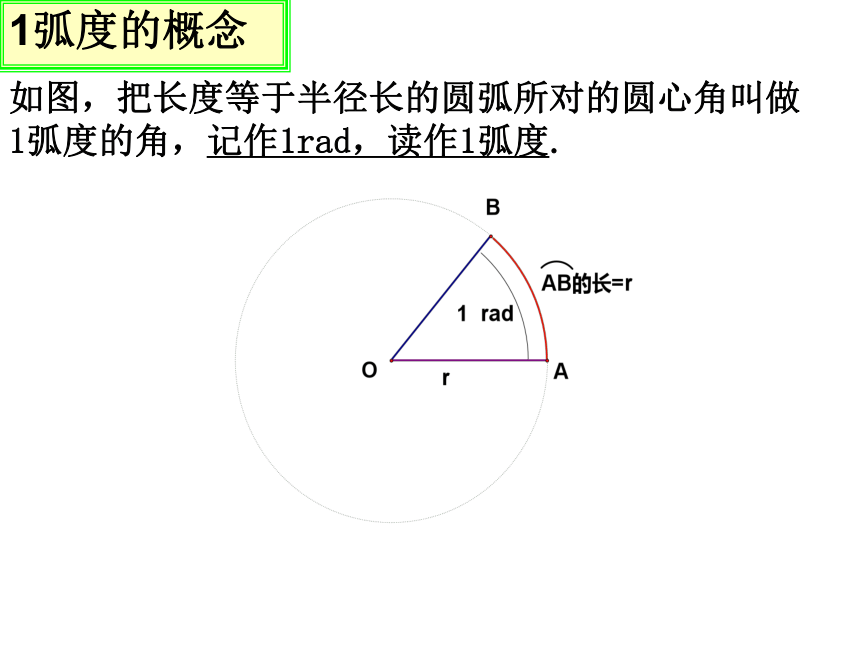
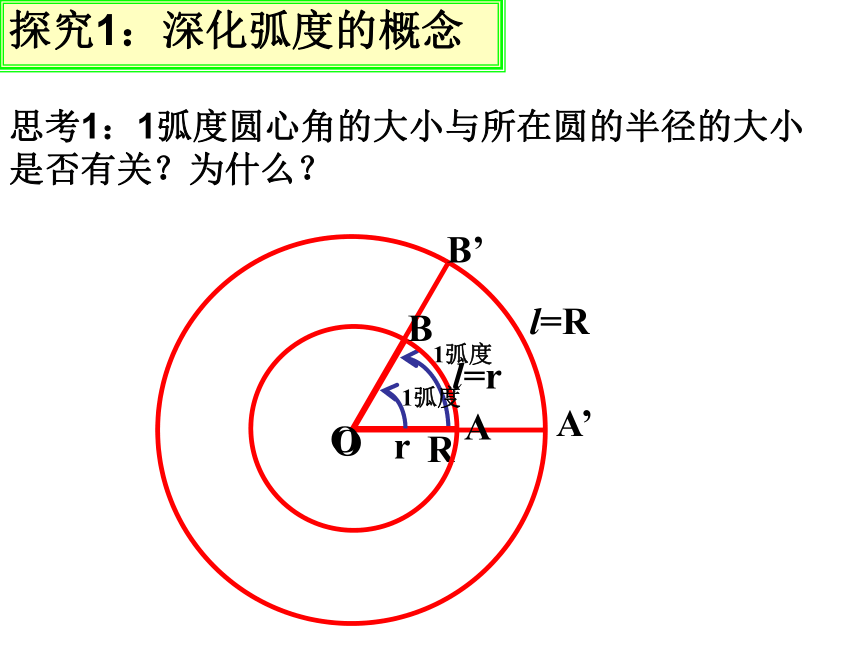
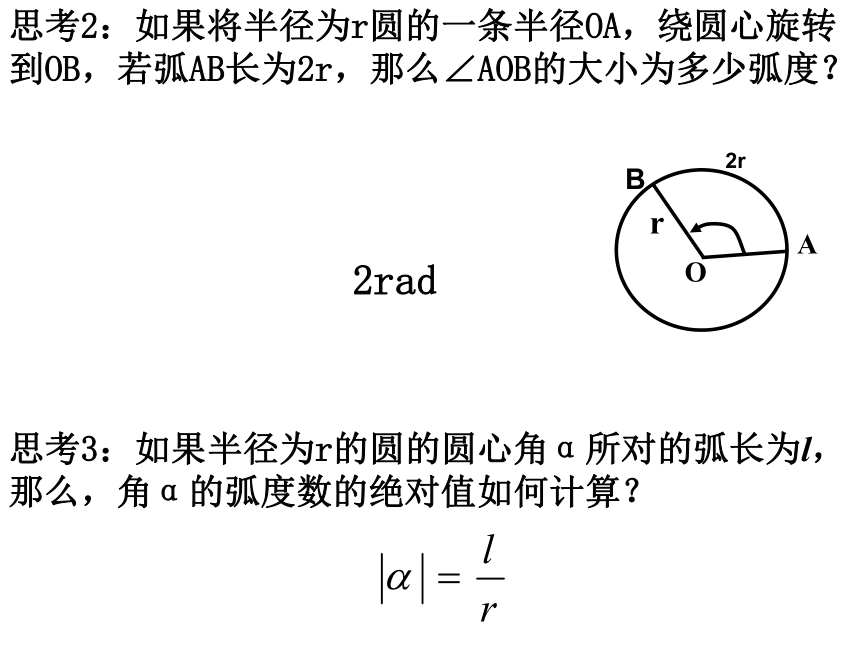
学习目标1、角度制:初中时我们用角度制度量角,1度的角等于周角的1/360。周角的1/360温故而知新如图,把长度等于半径长的圆弧所对的圆心角叫做1弧度的角,记作1rad,读作1弧度. 1弧度的概念思考1:1弧度圆心角的大小与所在圆的半径的大小是否有关?为什么?探究1:深化弧度的概念思考2:如果将半径为r圆的一条半径OA,绕圆心旋转到OB,若弧AB长为2r,那么∠AOB的大小为多少弧度?2radA思考3:如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值如何计算? 2r思考1:一个圆周角以度为单位度量是多少度?以弧度为单位度量是多少弧度?由此可得度与弧度有怎样的换算关系? 思考2:根据上述关系,1°等于多少弧度?1rad等于多少度? 360?=2? rad 180?=? rad 探究2:角度与弧度的换算思考3:根据度与弧度的换算关系,下表中各特殊角对应的数值分别是多少? 思考4:约定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0. 在弧度制下,角的集合与实数集R之间可以建立一个一一对应关系,这个对应关系是如何理解的? 正角
零角
负角正实数
零
负实数十进制思考1:角度制下,扇形的圆心角是n°,则扇形的面积是?思考2:类比思考1,在弧度制下,若扇形的圆心角是 弧度,则扇形的面积是?还有其它的表示方法么?探究3:与扇形有关的公式例题讲解1 把-300?化成弧度
跟踪练习 另解: 1、在半径为R的圆中,240o的圆心角所对的弧长为 ,面积为2R2的扇形的圆心角等于 弧度。所以 α=4.跟踪练习 2、已知扇形的周长为8cm,圆心角为2弧度,求该扇形的面积.解:设扇形的半径为r,弧长为 ,则有跟踪练习 当堂检测(限时5分钟,满分10分)2、 -144o3、-25o十进制小结角的度量角度制弧度制三角函数圆周角度360?六十进制圆周弧度2? 等价换
算区别六十进制十进制
弧度制与角度制的换算高中新课标人教B版必修4
1、理解弧度制的定义
2、熟练掌握角度与弧度之间的换算
3、熟练应用与扇形有关的公式
难点:对弧度制定义的理解
重点:熟练应用与扇形有关的公式
学习目标1、角度制:初中时我们用角度制度量角,1度的角等于周角的1/360。周角的1/360温故而知新如图,把长度等于半径长的圆弧所对的圆心角叫做1弧度的角,记作1rad,读作1弧度. 1弧度的概念思考1:1弧度圆心角的大小与所在圆的半径的大小是否有关?为什么?探究1:深化弧度的概念思考2:如果将半径为r圆的一条半径OA,绕圆心旋转到OB,若弧AB长为2r,那么∠AOB的大小为多少弧度?2radA思考3:如果半径为r的圆的圆心角α所对的弧长为l,那么,角α的弧度数的绝对值如何计算? 2r思考1:一个圆周角以度为单位度量是多少度?以弧度为单位度量是多少弧度?由此可得度与弧度有怎样的换算关系? 思考2:根据上述关系,1°等于多少弧度?1rad等于多少度? 360?=2? rad 180?=? rad 探究2:角度与弧度的换算思考3:根据度与弧度的换算关系,下表中各特殊角对应的数值分别是多少? 思考4:约定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为0. 在弧度制下,角的集合与实数集R之间可以建立一个一一对应关系,这个对应关系是如何理解的? 正角
零角
负角正实数
零
负实数十进制思考1:角度制下,扇形的圆心角是n°,则扇形的面积是?思考2:类比思考1,在弧度制下,若扇形的圆心角是 弧度,则扇形的面积是?还有其它的表示方法么?探究3:与扇形有关的公式例题讲解1 把-300?化成弧度
跟踪练习 另解: 1、在半径为R的圆中,240o的圆心角所对的弧长为 ,面积为2R2的扇形的圆心角等于 弧度。所以 α=4.跟踪练习 2、已知扇形的周长为8cm,圆心角为2弧度,求该扇形的面积.解:设扇形的半径为r,弧长为 ,则有跟踪练习 当堂检测(限时5分钟,满分10分)2、 -144o3、-25o十进制小结角的度量角度制弧度制三角函数圆周角度360?六十进制圆周弧度2? 等价换
算区别六十进制十进制
