人教B版数学必修4 1.2.2 单位圆与三角函数线(共22张ppt)
文档属性
| 名称 | 人教B版数学必修4 1.2.2 单位圆与三角函数线(共22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览






文档简介
课件22张PPT。1.2.2 单位圆与三角函数线(一)复习三角函数的坐标法定义◆课前复习?1、 有向线段的概念:带有方向的线段叫有向线段 ;
有向线段的数值由其长度大小和方向来决定。 如在数轴上,|OA|=3,|OB|=3,OA= ,
OB= ,AB=
-33-6(二)有向线段、单位圆的概念2.单位圆的概念 一般地,我们把半径为1的圆叫做单位圆,设单位圆的圆心与坐标原点重合,则单位圆与x轴的交点分别为
A(1,0),A’(-1,0).
而与y轴的交点分别为
B(0,1),B’(0,-1).(二)有向线段、单位圆的概念
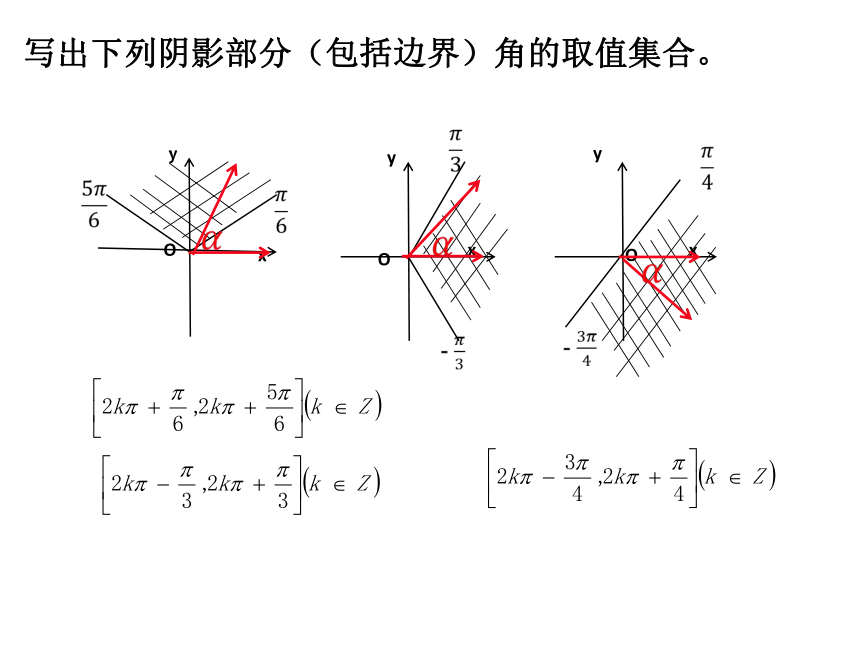
写出下列阴影部分(包括边界)角的取值集合。
?? 前面我们学习了三角函数的坐标法定义,三角函数在各象限内的符号,学习了任意角的三角函数。 由三角函数的定义我们知道,对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的,今天我们再来学习的任意角正弦、余弦、正切的另一种表示方法——◆学习目标
(一)知识与技能目标
1.了解有向线段的概念.
2.会用单位圆中的线段表示三角函数值.
(二)过程与方法目标
理解并掌握利用与单位圆有关的有向线段,将任意角的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来,并能作出三角函数线。
(三)情感态度与价值观目标
根据三角函数的定义导出三角函数线,培养数形结合思维习惯.
◆学习重点、难点
1.教学重点:三角函数线的探究与作法。
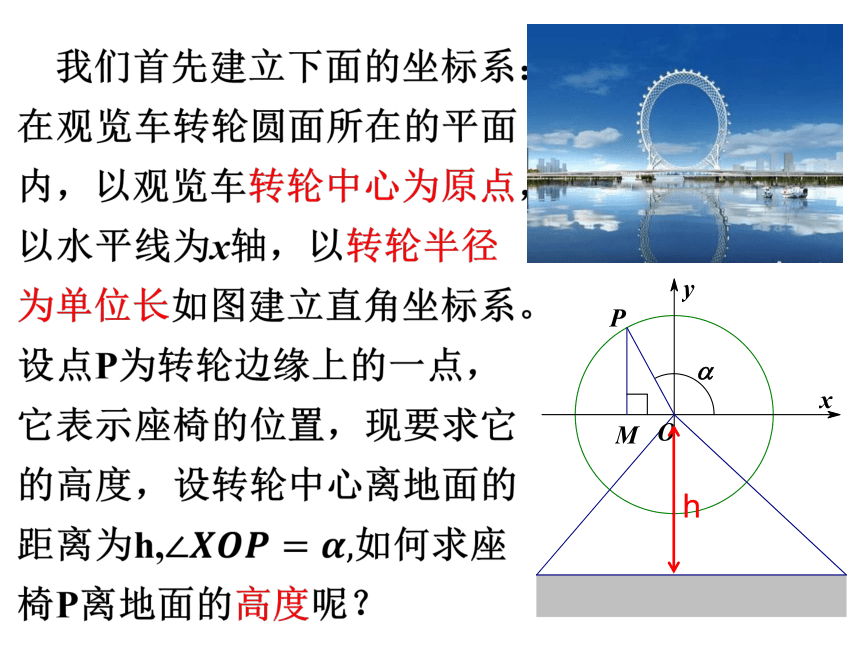
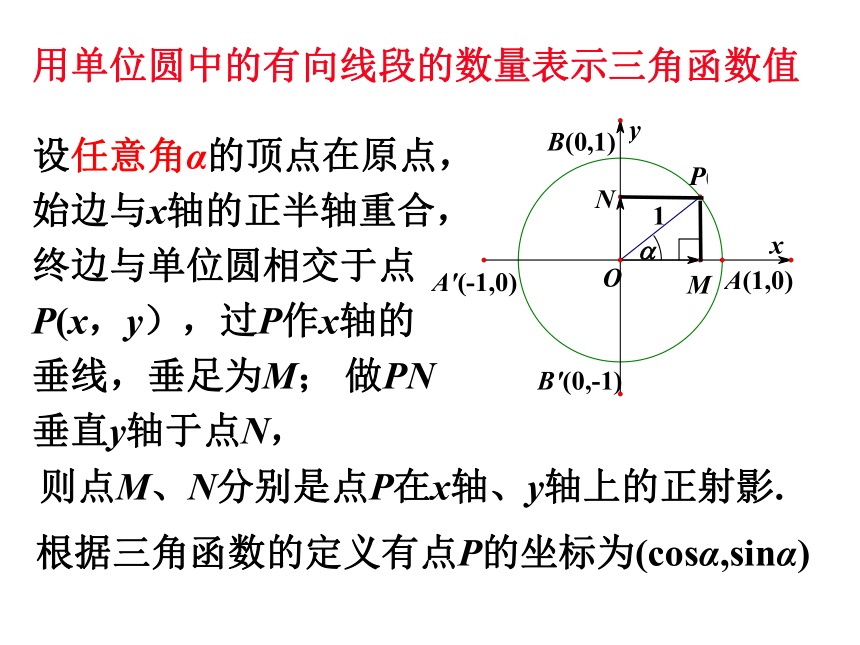
2.教学难点:利用三角函数线比较大小以及求角的大小关系对应?h设任意角α的顶点在原点,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M; 做PN垂直y轴于点N, 则点M、N分别是点P在x轴、y轴上的正射影.用单位圆中的有向线段的数量表示三角函数值根据三角函数的定义有点P的坐标为(cosα,sinα)根据三角函数的定义有点P的坐标为(cosα,sinα)其中cosα=OM,sinα=ON. 这就是说,角α的余弦和
正弦分别等于角α的终边
与单位圆交点的横坐标与
纵坐标. 以A为原点建立y’轴与y轴同向,y’轴与α角的终边(或其反向延长线)相交于点T(或T ’),则tanα=AT(或AT ’)思考:如何确定任意角的正切函数线呢?(四)例题当角的终边在x轴上时,
点P与点M重合,这时正弦线与正切线就变成了一点,数量为零,而余弦值OM=1或-1。
② 当角的终边在y轴上时,
正弦线的数量MP=1或-1,点O与点M重合余弦线变成了一点,它表示的数量为零,正切线不存在。
。 xy(M)α的终边TPMPMATA(Ⅰ)(Ⅱ)(Ⅲ)(Ⅳ)角α的终边在四个象限的情况思考2:?例3.利用三角函数线确定三角不等式的解集 1、解不等式2、 (五)小结1. 给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线。 正切线在过单位圆与x轴正方向的交点的切线上,为有向线段 。课堂小结3、三角函数线的应用:(1)利用三角函数线确定角的终边;
(2)利用三角函数线解三角方程或三角不等式,
用来确定角的集合。当堂检测BTATAh观览车座椅离地面的高度为:作业
第34页习题1-2A:4;
1-2B:5
有向线段的数值由其长度大小和方向来决定。 如在数轴上,|OA|=3,|OB|=3,OA= ,
OB= ,AB=
-33-6(二)有向线段、单位圆的概念2.单位圆的概念 一般地,我们把半径为1的圆叫做单位圆,设单位圆的圆心与坐标原点重合,则单位圆与x轴的交点分别为
A(1,0),A’(-1,0).
而与y轴的交点分别为
B(0,1),B’(0,-1).(二)有向线段、单位圆的概念
写出下列阴影部分(包括边界)角的取值集合。
?? 前面我们学习了三角函数的坐标法定义,三角函数在各象限内的符号,学习了任意角的三角函数。 由三角函数的定义我们知道,对于角α的各种三角函数我们都是用比值来表示的,或者说是用数来表示的,今天我们再来学习的任意角正弦、余弦、正切的另一种表示方法——◆学习目标
(一)知识与技能目标
1.了解有向线段的概念.
2.会用单位圆中的线段表示三角函数值.
(二)过程与方法目标
理解并掌握利用与单位圆有关的有向线段,将任意角的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来,并能作出三角函数线。
(三)情感态度与价值观目标
根据三角函数的定义导出三角函数线,培养数形结合思维习惯.
◆学习重点、难点
1.教学重点:三角函数线的探究与作法。
2.教学难点:利用三角函数线比较大小以及求角的大小关系对应?h设任意角α的顶点在原点,始边与x轴的正半轴重合,终边与单位圆相交于点P(x,y),过P作x轴的垂线,垂足为M; 做PN垂直y轴于点N, 则点M、N分别是点P在x轴、y轴上的正射影.用单位圆中的有向线段的数量表示三角函数值根据三角函数的定义有点P的坐标为(cosα,sinα)根据三角函数的定义有点P的坐标为(cosα,sinα)其中cosα=OM,sinα=ON. 这就是说,角α的余弦和
正弦分别等于角α的终边
与单位圆交点的横坐标与
纵坐标. 以A为原点建立y’轴与y轴同向,y’轴与α角的终边(或其反向延长线)相交于点T(或T ’),则tanα=AT(或AT ’)思考:如何确定任意角的正切函数线呢?(四)例题当角的终边在x轴上时,
点P与点M重合,这时正弦线与正切线就变成了一点,数量为零,而余弦值OM=1或-1。
② 当角的终边在y轴上时,
正弦线的数量MP=1或-1,点O与点M重合余弦线变成了一点,它表示的数量为零,正切线不存在。
。 xy(M)α的终边TPMPMATA(Ⅰ)(Ⅱ)(Ⅲ)(Ⅳ)角α的终边在四个象限的情况思考2:?例3.利用三角函数线确定三角不等式的解集 1、解不等式2、 (五)小结1. 给定任意一个角α,都能在单位圆中作出它的正弦线、余弦线、正切线。 正切线在过单位圆与x轴正方向的交点的切线上,为有向线段 。课堂小结3、三角函数线的应用:(1)利用三角函数线确定角的终边;
(2)利用三角函数线解三角方程或三角不等式,
用来确定角的集合。当堂检测BTATAh观览车座椅离地面的高度为:作业
第34页习题1-2A:4;
1-2B:5
