人教B版数学必修4 1.3.1 正弦型函数的图象与性质(共25张ppt)
文档属性
| 名称 | 人教B版数学必修4 1.3.1 正弦型函数的图象与性质(共25张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 431.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览



文档简介
课件25张PPT。函数y=Asin(ωx+φ)的图象2??oy=sinx3?
2?
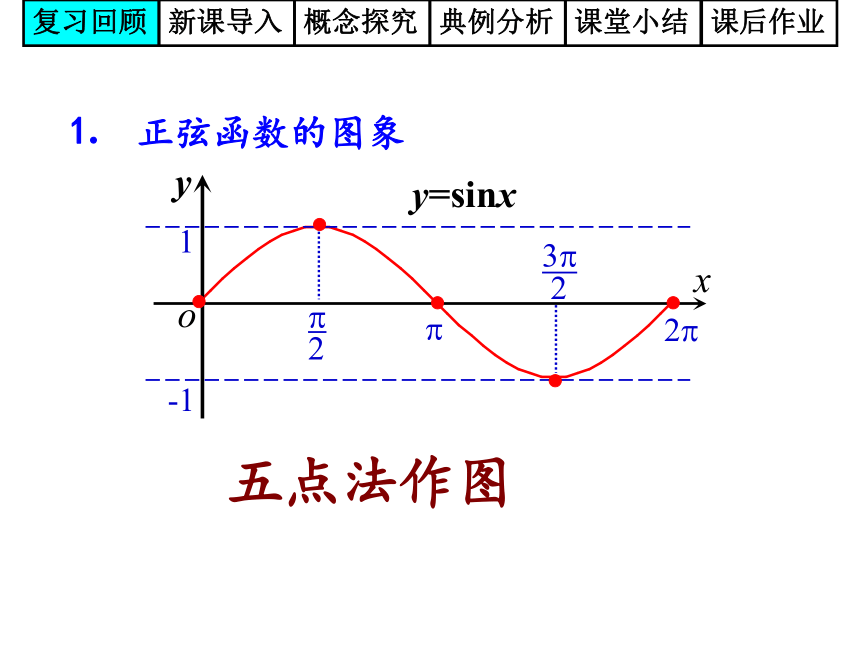
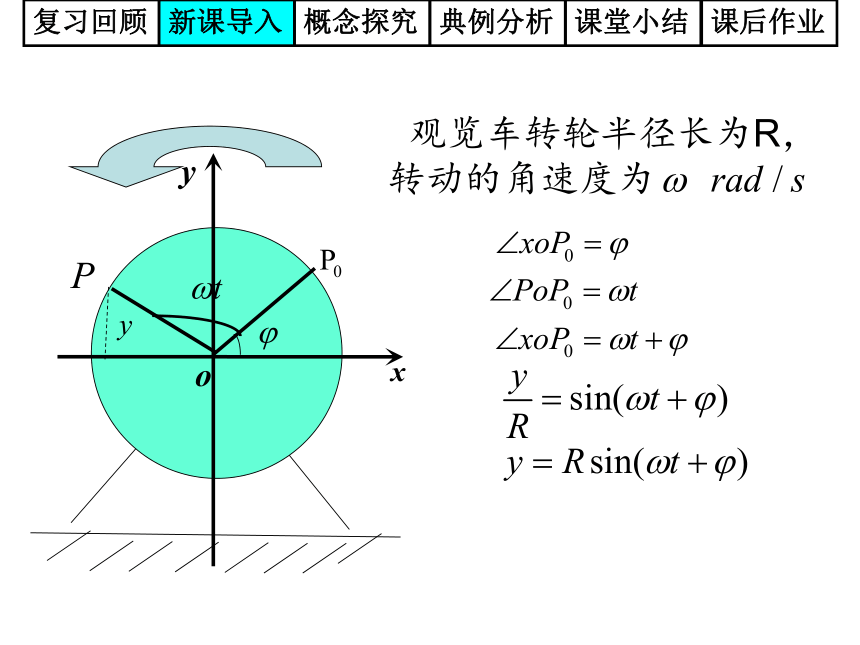
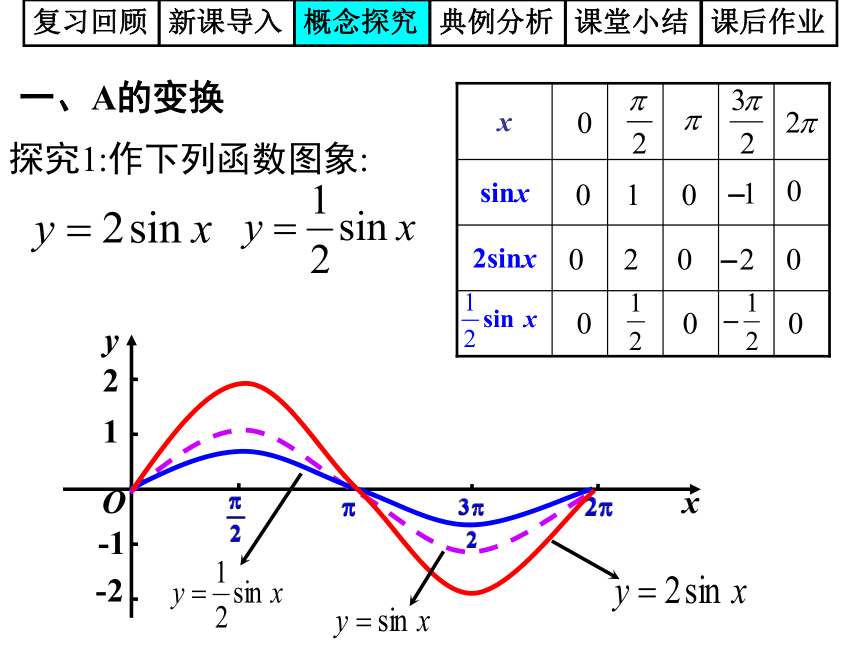
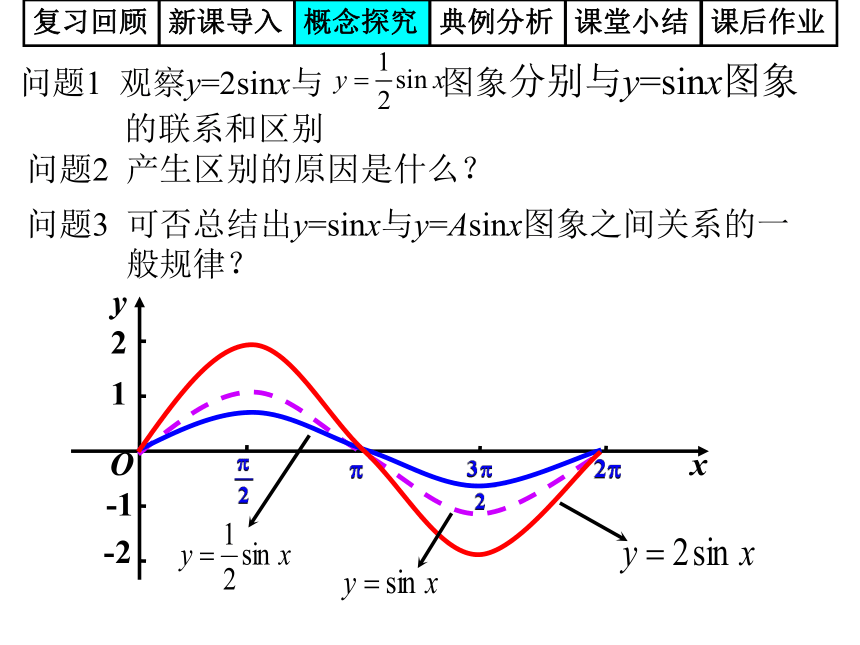
21-1⒈ 正弦函数的图象 五点法作图复习回顾新课导入概念探究典例分析课堂小结课后作业 观览车转轮半径长为R,转动的角速度为复习回顾新课导入概念探究典例分析课堂小结课后作业正弦型函数复习回顾新课导入概念探究典例分析课堂小结课后作业函数y=Asin(ωx+φ)的图象复习回顾新课导入概念探究典例分析课堂小结课后作业思考?和我们熟悉的正弦函数有什么联系?复习回顾新课导入概念探究典例分析课堂小结课后作业一、A的变换探究1:作下列函数图象:复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业问题1 观察y=2sinx与 图象分别与y=sinx图象
的联系和区别问题2 产生区别的原因是什么?问题3 可否总结出y=sinx与y=Asinx图象之间关系的一
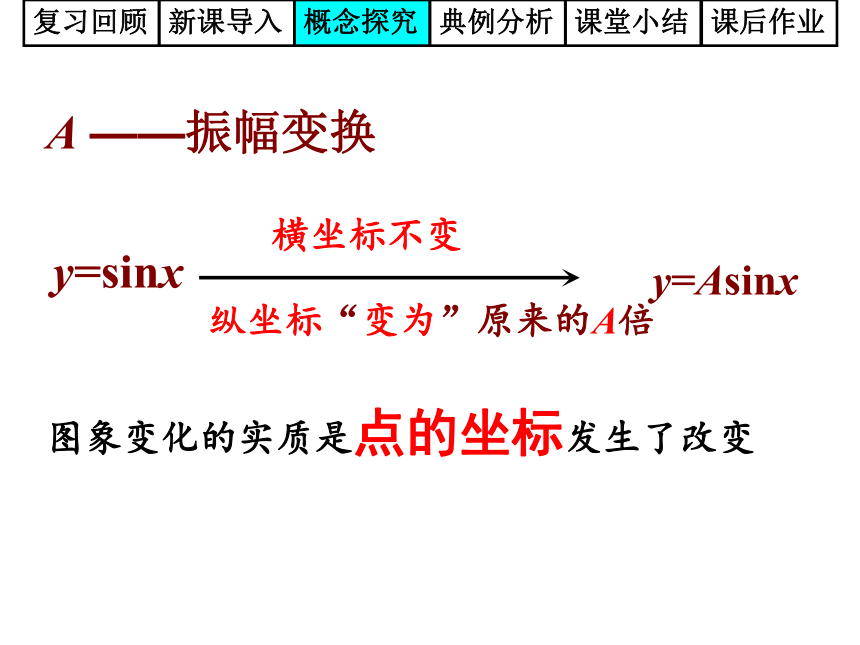
般规律?A ——振幅变换图象变化的实质是点的坐标发生了改变复习回顾新课导入概念探究典例分析课堂小结课后作业二、?的变换探究2:作函数 及 的图象.复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业问题1 观察y=sin2x与 图象分别与y=sinx图象的
联系和区别?问题2 产生区别的原因是什么?问题3 可否总结出y=sinx与y=sin?x图象之间关系的一
般规律?? ——周期变换2??3?4?3?
2复习回顾新课导入概念探究典例分析课堂小结课后作业x9?
45?
4?
42?
35?
3oy12??-1三、?的变换复习回顾新课导入概念探究典例分析课堂小结课后作业? ——相位变换复习回顾新课导入概念探究典例分析课堂小结课后作业典例分析复习回顾新课导入概念探究典例分析课堂小结课后作业例2 利用图像变换简图方法二方法一复习回顾新课导入概念探究典例分析课堂小结课后作业方法1:(按顺序变换)复习回顾新课导入概念探究典例分析课堂小结课后作业方法2:(按顺序变换)复习回顾新课导入概念探究典例分析课堂小结课后作业A1.已知函数复习回顾新课导入概念探究典例分析课堂小结课后作业课堂练习B复习回顾新课导入概念探究典例分析课堂小结课后作业 D复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业利用图像变换思考y=sinxy=sin(x+?)横坐标变为原来的1/?倍y=sin(?x+?)纵坐标变为原来的A倍y=Asin(?x+?)向左?>0 (向右?<0)方法1:(按 顺序变换)平移|?|个单位纵坐标不变横坐标不变复习回顾新课导入概念探究典例分析课堂小结课后作业y=sinxy=Asin(?x+?)小结:y=sinx横坐标变为原来的1/?倍y=sin?x纵坐标变为原来的A倍y=Asin(?x+?)y=sinxy=Asin(?x+?)小结:纵坐标不变横坐标不变方法2:(按 顺序变换)向左?>0 (向右?<0)平移|?|/?个单位复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业得到y=sinx的图象思考:
2?
21-1⒈ 正弦函数的图象 五点法作图复习回顾新课导入概念探究典例分析课堂小结课后作业 观览车转轮半径长为R,转动的角速度为复习回顾新课导入概念探究典例分析课堂小结课后作业正弦型函数复习回顾新课导入概念探究典例分析课堂小结课后作业函数y=Asin(ωx+φ)的图象复习回顾新课导入概念探究典例分析课堂小结课后作业思考?和我们熟悉的正弦函数有什么联系?复习回顾新课导入概念探究典例分析课堂小结课后作业一、A的变换探究1:作下列函数图象:复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业问题1 观察y=2sinx与 图象分别与y=sinx图象
的联系和区别问题2 产生区别的原因是什么?问题3 可否总结出y=sinx与y=Asinx图象之间关系的一
般规律?A ——振幅变换图象变化的实质是点的坐标发生了改变复习回顾新课导入概念探究典例分析课堂小结课后作业二、?的变换探究2:作函数 及 的图象.复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业问题1 观察y=sin2x与 图象分别与y=sinx图象的
联系和区别?问题2 产生区别的原因是什么?问题3 可否总结出y=sinx与y=sin?x图象之间关系的一
般规律?? ——周期变换2??3?4?3?
2复习回顾新课导入概念探究典例分析课堂小结课后作业x9?
45?
4?
42?
35?
3oy12??-1三、?的变换复习回顾新课导入概念探究典例分析课堂小结课后作业? ——相位变换复习回顾新课导入概念探究典例分析课堂小结课后作业典例分析复习回顾新课导入概念探究典例分析课堂小结课后作业例2 利用图像变换简图方法二方法一复习回顾新课导入概念探究典例分析课堂小结课后作业方法1:(按顺序变换)复习回顾新课导入概念探究典例分析课堂小结课后作业方法2:(按顺序变换)复习回顾新课导入概念探究典例分析课堂小结课后作业A1.已知函数复习回顾新课导入概念探究典例分析课堂小结课后作业课堂练习B复习回顾新课导入概念探究典例分析课堂小结课后作业 D复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业利用图像变换思考y=sinxy=sin(x+?)横坐标变为原来的1/?倍y=sin(?x+?)纵坐标变为原来的A倍y=Asin(?x+?)向左?>0 (向右?<0)方法1:(按 顺序变换)平移|?|个单位纵坐标不变横坐标不变复习回顾新课导入概念探究典例分析课堂小结课后作业y=sinxy=Asin(?x+?)小结:y=sinx横坐标变为原来的1/?倍y=sin?x纵坐标变为原来的A倍y=Asin(?x+?)y=sinxy=Asin(?x+?)小结:纵坐标不变横坐标不变方法2:(按 顺序变换)向左?>0 (向右?<0)平移|?|/?个单位复习回顾新课导入概念探究典例分析课堂小结课后作业复习回顾新课导入概念探究典例分析课堂小结课后作业得到y=sinx的图象思考:
