二年级上册数学一课一练-2.1乘法的初步认识 北京版(含答案)
文档属性
| 名称 | 二年级上册数学一课一练-2.1乘法的初步认识 北京版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 89.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-21 21:03:42 | ||
图片预览

文档简介
二年级上册数学一课一练-2.1乘法的初步认识
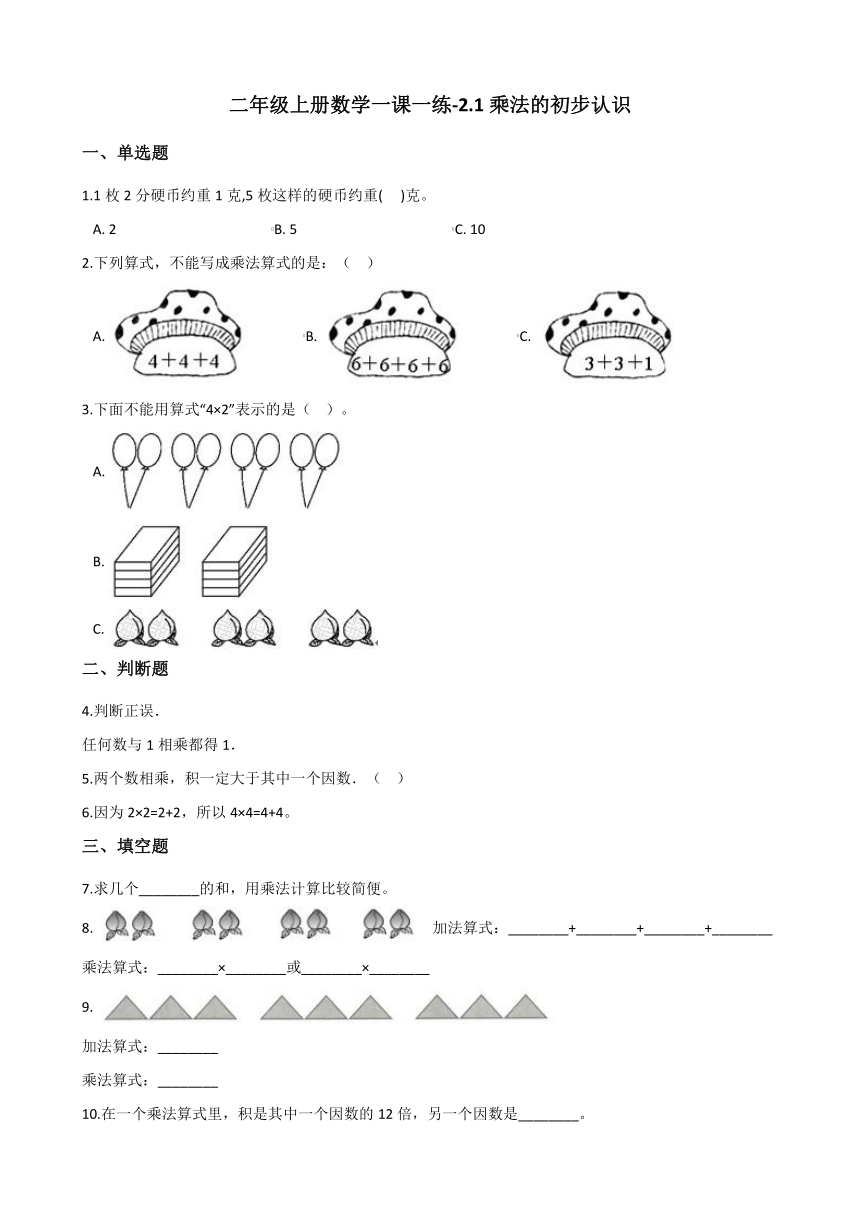
一、单选题
1.1枚2分硬币约重1克,5枚这样的硬币约重(??? )克。
A.?2?????????????????????????????????????????????B.?5?????????????????????????????????????????????C.?10
2.下列算式,不能写成乘法算式的是:(?? )
A.????????????????B.????????????????C.?
3.下面不能用算式“4×2”表示的是(?? )。
A.? B.? C.?
二、判断题
4.判断正误. 任何数与1相乘都得1.
5.两个数相乘,积一定大于其中一个因数.(?? )
6.因为2×2=2+2,所以4×4=4+4。
三、填空题
7.求几个________的和,用乘法计算比较简便。
8.加法算式:________+________+________+________ 乘法算式:________×________或________×________
9.
加法算式:________
乘法算式:________
10.在一个乘法算式里,积是其中一个因数的12倍,另一个因数是________。
四、解答题
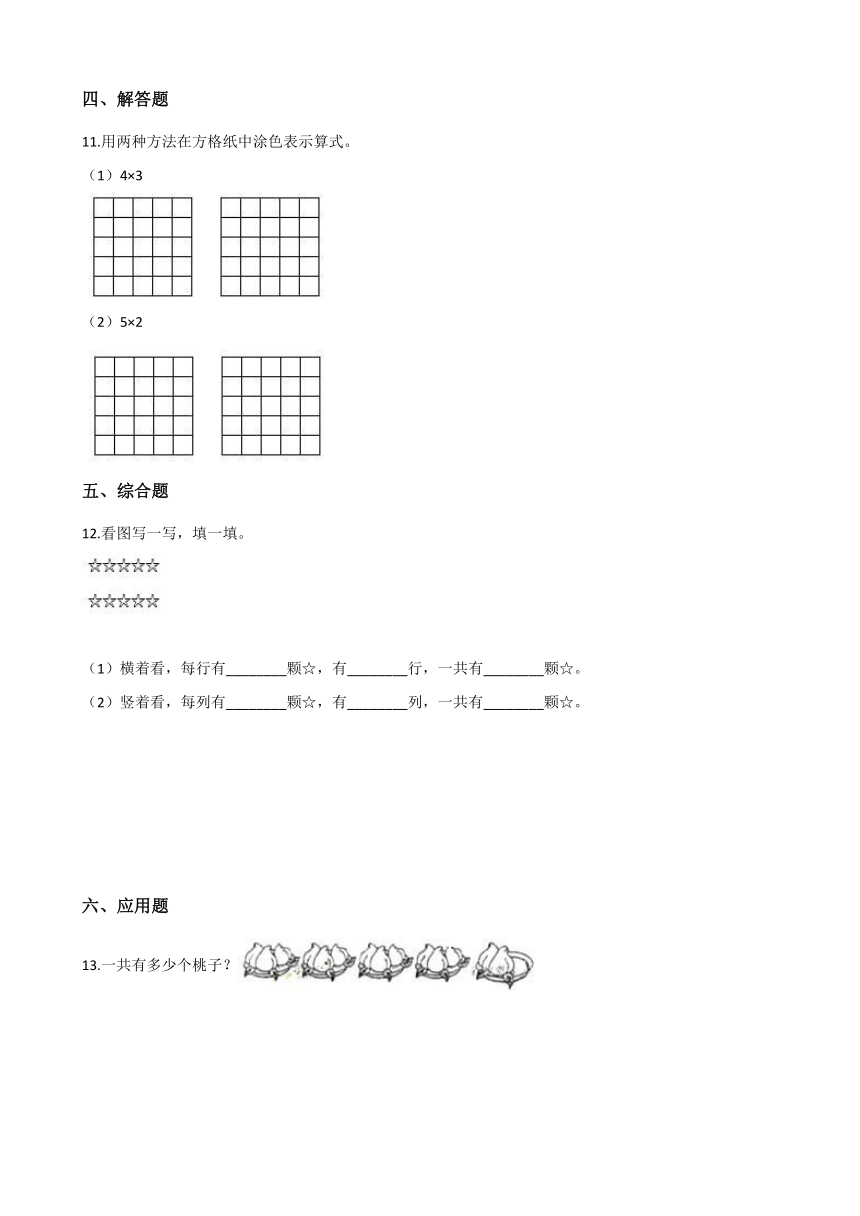
11.用两种方法在方格纸中涂色表示算式。
(1)4×3
(2)5×2
五、综合题
12.看图写一写,填一填。
(1)横着看,每行有________颗☆,有________行,一共有________颗☆。
(2)竖着看,每列有________颗☆,有________列,一共有________颗☆。
六、应用题
13.一共有多少个桃子???
参考答案
一、单选题
1.【答案】 B
【解析】【解答】1×5=5(克) 故答案为:B.
【分析】根据乘法的意义,求5枚这样的硬币重多少克,就是求5个1克是多少,用乘法计算.
2.【答案】 C
【解析】求几个相同加数的和,可以用乘法计算,可以改写成乘法算式.
4+4+4=4×3
6+6+6+6=4×6
3+3+1,因为几个加数不完全相同,所以不能改写成乘法算式.选C.
3.【答案】 C
【解析】【解答】解:A、表示4个2的和,能表示; B、表示2个4的和,能表示; C、表示3个2的和,乘法算式是2×3,不能表示。 故答案为:C。 【分析】乘法是求几个相同加数和的简便运算,“4×2”表示2个4的和,也表示4个2的和。
二、判断题
4.【答案】错误
【解析】【解答】任何数与1相乘都得原数,例如:0×1=0,原题说法错误. 故答案为:错误. 【分析】任何数与1相乘,积还是原数,例如0×1=0,12×1=12,据此判断.
5.【答案】 错误
【解析】【解答】例如:1×1=1,积等于两个因数,本题说法错误。 故答案为:错误。 【分析】一个数乘大于1的数,积大于这个数,乘小于1的数,积小于这个数,乘以1,积等于这个数。
6.【答案】 错误
【解析】【解答】2×2=2+2,4×4=4+4+4+4,原题说法错误. 故答案为:错误. 【分析】根据乘法的意义:求几个相同加数和的简便运算,用乘法计算,据此判断.
三、填空题
7.【答案】相同的数
【解析】【解答】根据定义填空求几个相同的数的和,用乘法计算比较简便, 【分析】根据题意填空。
8.【答案】2;2;2;2;2;4;4;2
【解析】【解答】解:加法算式:2+2+2+2;乘法算式:2×4或4×2 故答案为:2,2,2,2;2,4;4,2【分析】把每堆的个数相加写出加法算式,根据乘法的意义写出乘法算式,乘法是求几个相同加数和的简便运算。
9.【答案】 3+3+3=9;3×3=9
【解析】【解答】 加法算式:3+3+3=9; 乘法算式:3×3=9. 故答案为:3+3+3=9;3×3=9.
【分析】观察图可知,一组三角形有3个,一共有3组,要求一共有几个三角形,用加法计算时,将相同的加数相加; 用乘法计算时,用相同的加数与相同加数的个数相乘即可.
10.【答案】 12
【解析】【解答】 在一个乘法算式里,积是其中一个因数的12倍,另一个因数是12. 故答案为:12. 【分析】在乘法算式中,一个因数×另一个因数=积,根据条件“积是其中一个因数的12倍”可知:一个因数×12=积,据此可以得到另一个因数是几.
四、解答题
11.【答案】 (1) (2)
【解析】【分析】(1)4×3表示4个3相加是多少,每行涂3个正方形,涂4行;还可以表示3个4相加是多少,每行涂4个正方形,涂3行,据此作图; (2)5×2表示5个2相加是多少,每行涂2个正方形,涂5行;还可以表示2个5相加是多少,每行涂5个正方形,涂2行,据此作图.
五、综合题
12.【答案】 (1)5;2;10 (2)2;5;10
【解析】【解答】解:(1)横着看,每行有5颗☆,有2行,一共有5×2=10颗☆;(2)竖着看,每列有2颗☆,有5列,一共有2×5=10颗☆。 故答案为:(1)5;2;10;(2)2;5;10。 【分析】(1)横着看,一共有☆的颗数=每行有☆的颗数×行数,或一共有☆的颗数=行数×每行有☆的颗数,据此代入数据作答即可; (2)竖着看,一共有☆的颗数=每列有☆的颗数×列数,或一共有☆的颗数=列数×每列有☆的颗数,据此代入数据作答即可。
六、应用题
13.【答案】解:3×4+2=14(个)或3×5 - 1=14(个)答:一共有14个桃子。
【解析】【分析】用乘法计算出前4盘桃子的总数,再加上最后一盘的个数即可;或者把每盘都按照3个计算,再减去多算的一个桃子。
一、单选题
1.1枚2分硬币约重1克,5枚这样的硬币约重(??? )克。
A.?2?????????????????????????????????????????????B.?5?????????????????????????????????????????????C.?10
2.下列算式,不能写成乘法算式的是:(?? )
A.????????????????B.????????????????C.?
3.下面不能用算式“4×2”表示的是(?? )。
A.? B.? C.?
二、判断题
4.判断正误. 任何数与1相乘都得1.
5.两个数相乘,积一定大于其中一个因数.(?? )
6.因为2×2=2+2,所以4×4=4+4。
三、填空题
7.求几个________的和,用乘法计算比较简便。
8.加法算式:________+________+________+________ 乘法算式:________×________或________×________
9.
加法算式:________
乘法算式:________
10.在一个乘法算式里,积是其中一个因数的12倍,另一个因数是________。
四、解答题
11.用两种方法在方格纸中涂色表示算式。
(1)4×3
(2)5×2
五、综合题
12.看图写一写,填一填。
(1)横着看,每行有________颗☆,有________行,一共有________颗☆。
(2)竖着看,每列有________颗☆,有________列,一共有________颗☆。
六、应用题
13.一共有多少个桃子???
参考答案
一、单选题
1.【答案】 B
【解析】【解答】1×5=5(克) 故答案为:B.
【分析】根据乘法的意义,求5枚这样的硬币重多少克,就是求5个1克是多少,用乘法计算.
2.【答案】 C
【解析】求几个相同加数的和,可以用乘法计算,可以改写成乘法算式.
4+4+4=4×3
6+6+6+6=4×6
3+3+1,因为几个加数不完全相同,所以不能改写成乘法算式.选C.
3.【答案】 C
【解析】【解答】解:A、表示4个2的和,能表示; B、表示2个4的和,能表示; C、表示3个2的和,乘法算式是2×3,不能表示。 故答案为:C。 【分析】乘法是求几个相同加数和的简便运算,“4×2”表示2个4的和,也表示4个2的和。
二、判断题
4.【答案】错误
【解析】【解答】任何数与1相乘都得原数,例如:0×1=0,原题说法错误. 故答案为:错误. 【分析】任何数与1相乘,积还是原数,例如0×1=0,12×1=12,据此判断.
5.【答案】 错误
【解析】【解答】例如:1×1=1,积等于两个因数,本题说法错误。 故答案为:错误。 【分析】一个数乘大于1的数,积大于这个数,乘小于1的数,积小于这个数,乘以1,积等于这个数。
6.【答案】 错误
【解析】【解答】2×2=2+2,4×4=4+4+4+4,原题说法错误. 故答案为:错误. 【分析】根据乘法的意义:求几个相同加数和的简便运算,用乘法计算,据此判断.
三、填空题
7.【答案】相同的数
【解析】【解答】根据定义填空求几个相同的数的和,用乘法计算比较简便, 【分析】根据题意填空。
8.【答案】2;2;2;2;2;4;4;2
【解析】【解答】解:加法算式:2+2+2+2;乘法算式:2×4或4×2 故答案为:2,2,2,2;2,4;4,2【分析】把每堆的个数相加写出加法算式,根据乘法的意义写出乘法算式,乘法是求几个相同加数和的简便运算。
9.【答案】 3+3+3=9;3×3=9
【解析】【解答】 加法算式:3+3+3=9; 乘法算式:3×3=9. 故答案为:3+3+3=9;3×3=9.
【分析】观察图可知,一组三角形有3个,一共有3组,要求一共有几个三角形,用加法计算时,将相同的加数相加; 用乘法计算时,用相同的加数与相同加数的个数相乘即可.
10.【答案】 12
【解析】【解答】 在一个乘法算式里,积是其中一个因数的12倍,另一个因数是12. 故答案为:12. 【分析】在乘法算式中,一个因数×另一个因数=积,根据条件“积是其中一个因数的12倍”可知:一个因数×12=积,据此可以得到另一个因数是几.
四、解答题
11.【答案】 (1) (2)
【解析】【分析】(1)4×3表示4个3相加是多少,每行涂3个正方形,涂4行;还可以表示3个4相加是多少,每行涂4个正方形,涂3行,据此作图; (2)5×2表示5个2相加是多少,每行涂2个正方形,涂5行;还可以表示2个5相加是多少,每行涂5个正方形,涂2行,据此作图.
五、综合题
12.【答案】 (1)5;2;10 (2)2;5;10
【解析】【解答】解:(1)横着看,每行有5颗☆,有2行,一共有5×2=10颗☆;(2)竖着看,每列有2颗☆,有5列,一共有2×5=10颗☆。 故答案为:(1)5;2;10;(2)2;5;10。 【分析】(1)横着看,一共有☆的颗数=每行有☆的颗数×行数,或一共有☆的颗数=行数×每行有☆的颗数,据此代入数据作答即可; (2)竖着看,一共有☆的颗数=每列有☆的颗数×列数,或一共有☆的颗数=列数×每列有☆的颗数,据此代入数据作答即可。
六、应用题
13.【答案】解:3×4+2=14(个)或3×5 - 1=14(个)答:一共有14个桃子。
【解析】【分析】用乘法计算出前4盘桃子的总数,再加上最后一盘的个数即可;或者把每盘都按照3个计算,再减去多算的一个桃子。
