沪科版八年级上数学14.2全等三角形的判定(一)课件(25张ppt)
文档属性
| 名称 | 沪科版八年级上数学14.2全等三角形的判定(一)课件(25张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 919.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-21 10:25:52 | ||
图片预览




文档简介
(共25张PPT)
14.2三角形全等判定(1)
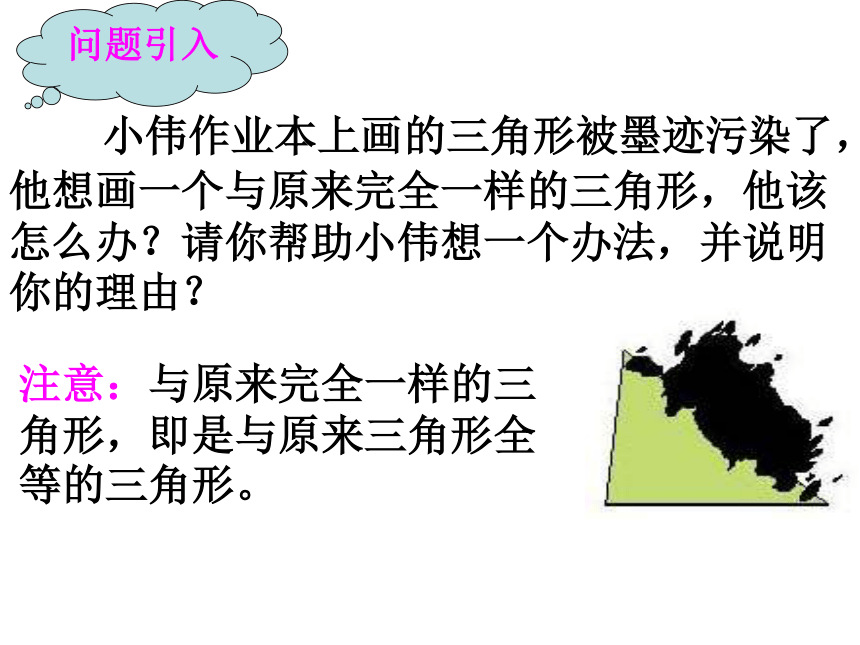
小伟作业本上画的三角形被墨迹污染了,他想画一个与原来完全一样的三角形,他该怎么办?请你帮助小伟想一个办法,并说明你的理由?
注意:与原来完全一样的三角形,即是与原来三角形全等的三角形。
问题引入
想一想:
要画一个三角形与小伟画的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
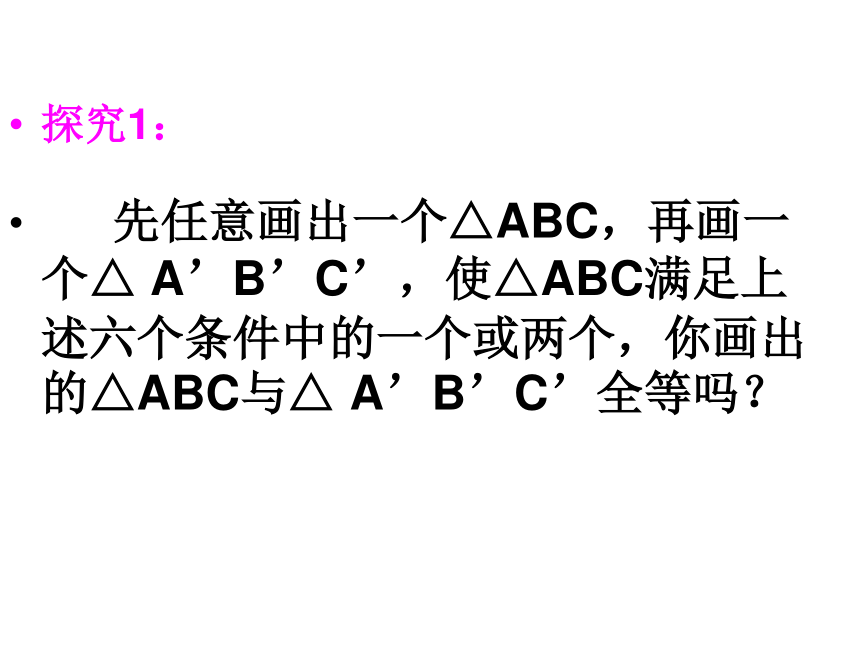
探究1:
先任意画出一个△ABC,再画一个△ A’B’C’,使△ABC满足上述六个条件中的一个或两个,你画出的△ABC与△ A’B’C’全等吗?
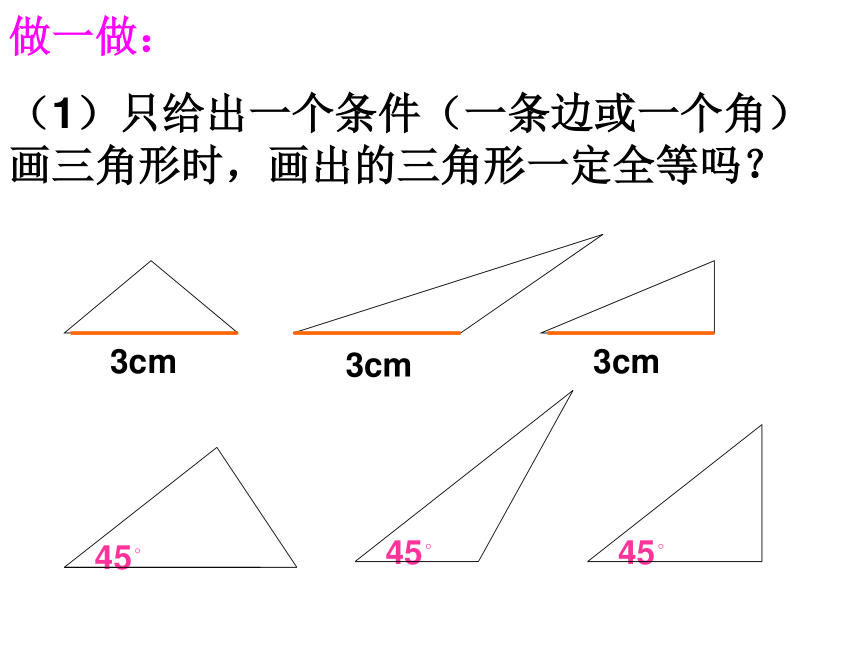
做一做:
(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
1)三角形的一个内角为30°,一条边为3cm;
2) 三角形的两个内角分别为30°和45°;
3)三角形的两条边分别为4cm和6cm.
按下面的条件画三角形,画完后小组内交流,看所画的三角形是否全等。(其它条件不确定)
(2)给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?
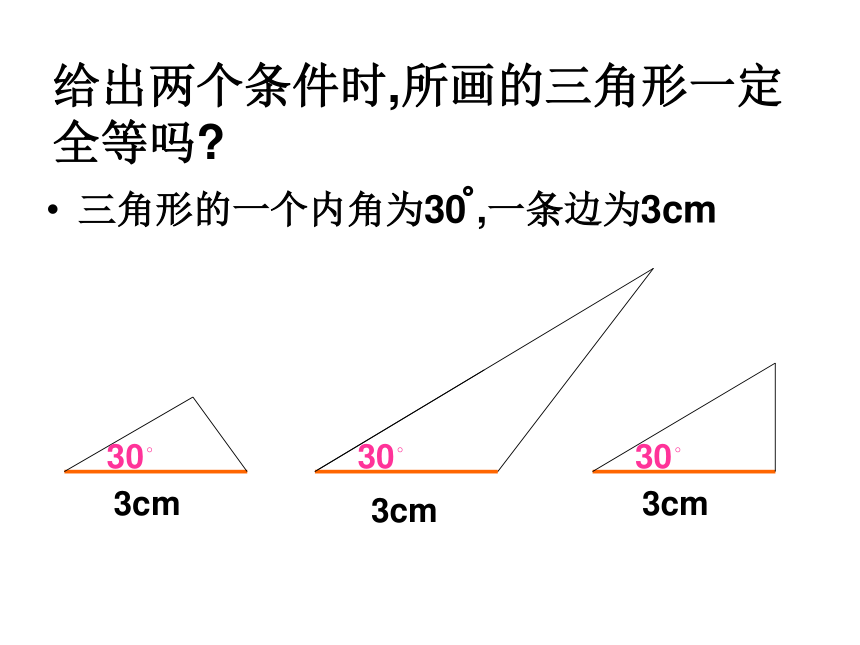
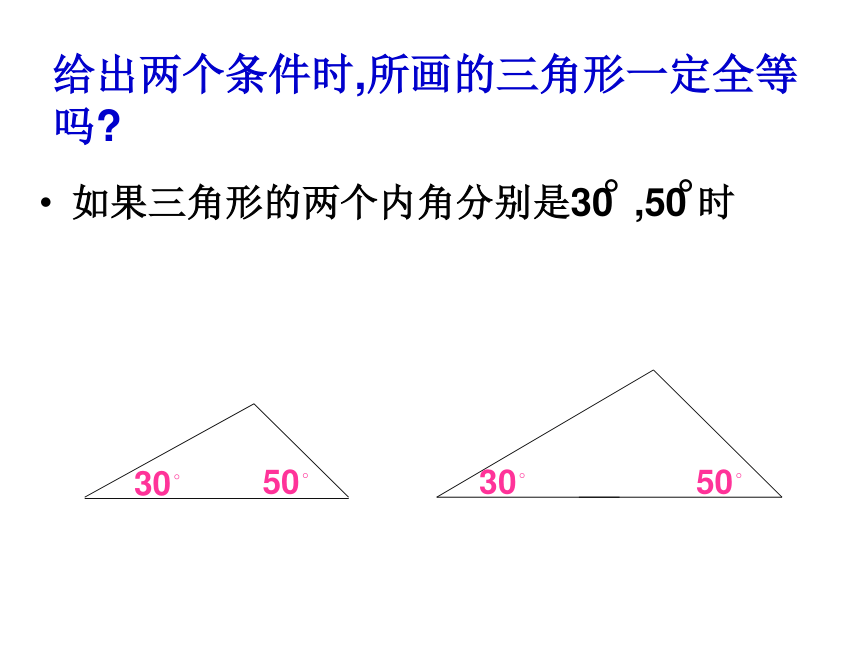
给出两个条件时,所画的三角形一定全等吗?
三角形的一个内角为30 ,一条边为3cm
30?
给出两个条件时,所画的三角形一定全等吗?
如果三角形的两个内角分别是30 ,50 时
30?
30?
50?
50?
给出两个条件时,所画的三角形一定全等吗?
如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
只给两个条件作出三角形,不能保证所画出的三角形一定全等。
(3)给出三个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?
(1)三边相等
(2) 三角相等
(3)两边一角(两边和它们的夹角;两边和其中一边的对角)
(4)两角一边(两角和它们的夹边;两角和其中一角的对边)
我们今天专题研究有两条边和它们的夹角对应相等的
两个三角形是否全等?
做一做:
已知:△ABC
求作:△DEF,DE=AB,∠E=∠B,EF=BC
将所作的△DEF与△ABC叠一叠,看看它们是否完全重合?由此你能得到什么结论?
A
B
C
全等三角形判定方法一(基本事实):
两边和它们的夹角对应相等的两个三角形全等。简记为“边角边”或“SAS”(S表示边,A表示角)。
A
B
D
E
C
第2题
B
A
D
C
2
1
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC?
∠ACB=∠DCE
BC=EC
△ACB≌△DCE(SAS)
AB=DE(全等三角形的对应边相等)
E
C
B
A
D
想一想:
如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。
范例学习
例:已知:如图,AD∥BC AD=BC
求证:
证明:∵AD∥BC(已知)
∴∠DAC=∠BCA(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC(已知)
∠DAC=∠BCA(已证)
AC=CA(公共边)
∴△ADC≌△CBA(SAS)
△ADC≌△CBA
准备条件
指出范围
列举条件
得出结论
例题讲解1:
如图,已知AD∥ BC,AD=BC.你能说明△ABC与△CDA全等吗?你能说明AB=CD,AB∥CD吗?为什么?
A
B
C
D
例2(2007金华):如图, A,E,B,D在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC和ΔDEF, (1)求证: ΔABC≌ΔDEF;
(1)证明:∵AC∥DF(已知) ∴∠A=∠D (两直线平行,内错角相等)
∴ΔABC≌ΔDEF(SAS)
在ΔABC和ΔDEF中
∵BE=EB(公共边)
又∵ AC∥ DB(已知) ∠DBE=∠CEB (两直线平行,内错角相等)
例3 (2006湖北黄冈):如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE
证明:∵AC=2DB,AE=EC (已知) ∴DB=EC
DB=EC
∠DBE=∠CEB
BE=EB
∴ ΔDBE≌ΔCEB(SAS) ∴ BC=DE (全等三角形的对应边相等)
4:如图,已知△ABC中,BE和CD分别为 ∠ABC和∠ABC的平分线,且BD = CE,∠1 = ∠2。说明BE = CD的理由。
解:∵∠DBC = 2∠1,∠ECB = 2∠2
(角平分线的定义)
∠1 = ∠2∴∠DBC = ∠ECB
在△DBC和△ECB中
BD = CE(已知)
∠DBC = ∠ECB
BC = CB(公共边)
∴ △DBC≌△ECB(SAS)
∴BE = CD(全等三角形的对应边相等)
大显身手 : 1.小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
证明:在△EDH和△FDH中,
ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)
∴ △EDH≌△FDH(SAS)
∴EH=FH(全等三角形的对应边相等)
∵
B
C
D
E
A
2.如图,已知AB=AC,AD=AE。
求证:∠B=∠C
C
E
A
B
A
D
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
∵
F
E
D
C
B
A
3.如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?
解:全等。∵BD=EC(已知) ∴BD-CD=EC-CD。即BC=ED
在△ABC与△FED中
∴△ABC≌△FED(SAS)
AC∥FD吗?为什么?
∴∠1=∠2( )
∴∠3=∠4( )
∴AC∥FD(内错角相等,两直线平行
4
3
2
1
小结:
1.今天我们经历了画图验证两个三角形全等的过程,探索出两个三角形全等的方法之一“两边和它们的夹角对应相等的两个三角形全等”,我们可以利用它来判别两个三角形是否全等。
2.我们可以通过证明三角形全等的方法来证明线段相等或角相等。
3.证明两个三角形全等的思路:首先分析条件,观察已经具备了什么条件,然后以已具备的条件为基础,根据全等三角形的判定方法,来确定还需要证明哪些边或角对应相等,再设法证明这些边和角相等。
再 见
祝同学们学习进步
14.2三角形全等判定(1)
小伟作业本上画的三角形被墨迹污染了,他想画一个与原来完全一样的三角形,他该怎么办?请你帮助小伟想一个办法,并说明你的理由?
注意:与原来完全一样的三角形,即是与原来三角形全等的三角形。
问题引入
想一想:
要画一个三角形与小伟画的三角形全等。需要几个与边或角的大小有关的条件?只知道一个条件(一角或一边)行吗?两个条件呢?三个条件呢?
让我们一起来探索三角形全等的条件
探究1:
先任意画出一个△ABC,再画一个△ A’B’C’,使△ABC满足上述六个条件中的一个或两个,你画出的△ABC与△ A’B’C’全等吗?
做一做:
(1)只给出一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?
1)三角形的一个内角为30°,一条边为3cm;
2) 三角形的两个内角分别为30°和45°;
3)三角形的两条边分别为4cm和6cm.
按下面的条件画三角形,画完后小组内交流,看所画的三角形是否全等。(其它条件不确定)
(2)给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?
给出两个条件时,所画的三角形一定全等吗?
三角形的一个内角为30 ,一条边为3cm
30?
给出两个条件时,所画的三角形一定全等吗?
如果三角形的两个内角分别是30 ,50 时
30?
30?
50?
50?
给出两个条件时,所画的三角形一定全等吗?
如果三角形的两边分别为4cm,6cm 时
6cm
6cm
4cm
4cm
只给两个条件作出三角形,不能保证所画出的三角形一定全等。
(3)给出三个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?
(1)三边相等
(2) 三角相等
(3)两边一角(两边和它们的夹角;两边和其中一边的对角)
(4)两角一边(两角和它们的夹边;两角和其中一角的对边)
我们今天专题研究有两条边和它们的夹角对应相等的
两个三角形是否全等?
做一做:
已知:△ABC
求作:△DEF,DE=AB,∠E=∠B,EF=BC
将所作的△DEF与△ABC叠一叠,看看它们是否完全重合?由此你能得到什么结论?
A
B
C
全等三角形判定方法一(基本事实):
两边和它们的夹角对应相等的两个三角形全等。简记为“边角边”或“SAS”(S表示边,A表示角)。
A
B
D
E
C
第2题
B
A
D
C
2
1
小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结ED,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。
AC=DC?
∠ACB=∠DCE
BC=EC
△ACB≌△DCE(SAS)
AB=DE(全等三角形的对应边相等)
E
C
B
A
D
想一想:
如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。
范例学习
例:已知:如图,AD∥BC AD=BC
求证:
证明:∵AD∥BC(已知)
∴∠DAC=∠BCA(两直线平行,内错角相等)
在△ADC和△CBA中,
AD=BC(已知)
∠DAC=∠BCA(已证)
AC=CA(公共边)
∴△ADC≌△CBA(SAS)
△ADC≌△CBA
准备条件
指出范围
列举条件
得出结论
例题讲解1:
如图,已知AD∥ BC,AD=BC.你能说明△ABC与△CDA全等吗?你能说明AB=CD,AB∥CD吗?为什么?
A
B
C
D
例2(2007金华):如图, A,E,B,D在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC和ΔDEF, (1)求证: ΔABC≌ΔDEF;
(1)证明:∵AC∥DF(已知) ∴∠A=∠D (两直线平行,内错角相等)
∴ΔABC≌ΔDEF(SAS)
在ΔABC和ΔDEF中
∵BE=EB(公共边)
又∵ AC∥ DB(已知) ∠DBE=∠CEB (两直线平行,内错角相等)
例3 (2006湖北黄冈):如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE
证明:∵AC=2DB,AE=EC (已知) ∴DB=EC
DB=EC
∠DBE=∠CEB
BE=EB
∴ ΔDBE≌ΔCEB(SAS) ∴ BC=DE (全等三角形的对应边相等)
4:如图,已知△ABC中,BE和CD分别为 ∠ABC和∠ABC的平分线,且BD = CE,∠1 = ∠2。说明BE = CD的理由。
解:∵∠DBC = 2∠1,∠ECB = 2∠2
(角平分线的定义)
∠1 = ∠2∴∠DBC = ∠ECB
在△DBC和△ECB中
BD = CE(已知)
∠DBC = ∠ECB
BC = CB(公共边)
∴ △DBC≌△ECB(SAS)
∴BE = CD(全等三角形的对应边相等)
大显身手 : 1.小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,将上述条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流。
证明:在△EDH和△FDH中,
ED=FD(已知)
∠EDH=∠FDH(已知)
DH=DH(公共边)
∴ △EDH≌△FDH(SAS)
∴EH=FH(全等三角形的对应边相等)
∵
B
C
D
E
A
2.如图,已知AB=AC,AD=AE。
求证:∠B=∠C
C
E
A
B
A
D
证明:在△ABD和△ACE中
∴△ABD≌△ACE(SAS)
∴∠B=∠C(全等三角形
对应角相等)
∵
F
E
D
C
B
A
3.如图,∠B=∠E,AB=EF,BD=EC,那么△ABC与 △FED全等吗?为什么?
解:全等。∵BD=EC(已知) ∴BD-CD=EC-CD。即BC=ED
在△ABC与△FED中
∴△ABC≌△FED(SAS)
AC∥FD吗?为什么?
∴∠1=∠2( )
∴∠3=∠4( )
∴AC∥FD(内错角相等,两直线平行
4
3
2
1
小结:
1.今天我们经历了画图验证两个三角形全等的过程,探索出两个三角形全等的方法之一“两边和它们的夹角对应相等的两个三角形全等”,我们可以利用它来判别两个三角形是否全等。
2.我们可以通过证明三角形全等的方法来证明线段相等或角相等。
3.证明两个三角形全等的思路:首先分析条件,观察已经具备了什么条件,然后以已具备的条件为基础,根据全等三角形的判定方法,来确定还需要证明哪些边或角对应相等,再设法证明这些边和角相等。
再 见
祝同学们学习进步
