人教版八年级数学上册第十三章 轴对称13.1轴对称同步练习(2份 含答案)
文档属性
| 名称 | 人教版八年级数学上册第十三章 轴对称13.1轴对称同步练习(2份 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-21 00:00:00 | ||
图片预览

文档简介
13.1轴对称(1)
一.选择
1.下列图形中,是轴对称图形的是 ( )
A B C D
2.如图13 -1-1所示的五角星是轴对称图形,它的对称轴共有 ( )
A.1条 B.3条 C.5条 D.无数条
3.如图13 -1-2.在△ABC中,BA=BC,∠ABC= 120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC= 24,则△BMN的周长是( )
A.36 B.24 C.18 D.16
4.如图13 -1-3,在△ABC中,AB =AC= 20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35 cm,则BC的长为 ( )
A.5 cm B.10 cm C.15 cm D.17.5 cm
5.如图13 -1-4,在暑假期间,某学校对其校内的高中楼(图中的点A),临建楼(图中的点日)和图书馆(图中的点C)进行装修,装修工人小明需要放置一批装修物资,使得装修物资到点A.点召和点C的距离相等,则装修物资应该放置在 ( )
AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在∠A、∠B两内角平分线的交点处
D.在AC、BC两边垂直平分线的交点处
6.如图13 -1-6,△ABC与△DEF关于直线MN成轴对称,则以下结论中不一定正确的是 ( )
A.A、D的连线被MN垂直平分 B.AB∥DF C.AB =DE D.∠B= ∠E
7.下列说法正确的是 ( )
A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形
B.任何一个图形都有对称轴,有的图形不止一条对称轴
C.平面上两个大小、形状完全一样的图形一定关于某直线对称
D.如果△ABC和△EFG成轴对称,那么它们的面积一定相等
二、填空
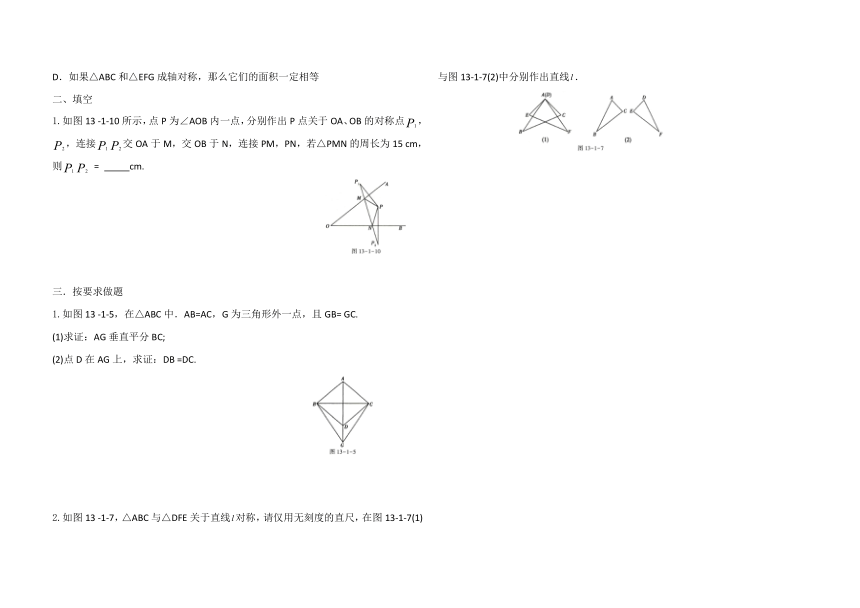
1.如图13 -1-10所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点,,连接交OA于M,交OB于N,连接PM,PN,若△PMN的周长为15 cm,则 = cm.
三.按要求做题
1.如图13 -1-5,在△ABC中.AB=AC,G为三角形外一点,且GB= GC.
(1)求证:AG垂直平分BC;
(2)点D在AG上,求证:DB =DC.
2.如图13 -1-7,△ABC与△DFE关于直线对称,请仅用无刻度的直尺,在图13-1-7(1)与图13-1-7(2)中分别作出直线.
13.1轴对称(2)
一.选择
1.图13 -1-8中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是 ( )
(1) B(2) C.(3) D.(4)
2.如图13 -1-9,在四边形ABCD中,边AB与AD关于AC对称,则下面结论正确的是 ( )
①CA平分∠BCD; ②AC平分∠BAD; ③BD⊥AC; ④BD平分AC.
①② B.①②③ C.②③④ D.①②③④
3.图书馆的标志是浓缩了图书馆文化的符号,下列图书馆标志中,不是轴对称图形的是 ( )
A B C D
4.如图13 -1-11,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3 cm,△ADC的周长为9 cm,则△ABC的周长是( )
A.10 cm B.12 cm C.15 cm D.17 cm
5.下列图形中,不是轴对称图形的是 ( )
A B C D
6.图13 -1-14是由“○”和“□”组成的轴对称图形,该图形的对称轴是直线 ( )
B. C. D.
7.如图13 -1- 15,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为 ( )
A.12 B.13 C.14 D.15
二、填空
1.如图13 -1-12,直线m是多边形ABCDE的对称轴,其中∠A= 120°,∠B= 110°,那么∠BCD的度数为 .
2.如图13 -1- 13,直线AD是△ABC的一条对称轴,AC=8 cm,DC=4 cm,则△ABC的周长为 cm.
3.如图13 -1 - 16,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是 .
三、按要求做题
1.请你用3种方法,将四块如图13 -1-17所示的小正方形纸板拼成一个大的正方形,并且使拼咸的大正方形是至少有两条对称轴的轴对称图形.
2.如图13 -1-18.已知△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A"B"C"关于直线EF对称.
(1)画出直线EF;
(2)若直线MN与EF相交于点O,试探究∠BOB"与直线MN、EF所夹角α的数量关系.
13.1轴对称(1)答案:
1.D选项A,B.C中的图形沿着某条直线折叠,直线两旁的部
分不能重合,所以选项A,B,C中的图形都不是轴对称图形,
故选D.
2.C五角星的对称轴共有5条,故选C.
3.B∵直线ME为线段AB的垂直平分线,
∴MA= MB,又直线NF为线段BC的垂直平分线,
∴NB =NC,∴△BMN的周长=BM+MN+BN =AM+MN+NC=AC= 24,故选B.
4.C∵DE垂直平分AB.∴AD=BD.
又∵△DBC的周长=BC+BD+CD=35 cm,
∴BC+AD+CD= 35 cm.
∵AC=AD+DC=20 cm,
∴BC= 35-20= 15 cm.故选C.
D
作AC、BC两边的垂直平分线,它们的交点是P,由线段的
垂直平分线的性质,知PA =PB =PC.故选D.
B
△ABC与△DEF关于直线MN成轴对稼,所以A、D的
连线被MN垂直平分,故结论正确;由已知条件无法判定
AB与DF平行,故结论不一定正确;△ABC与△DEF关于
直线MN成轴对称,则△ABC≌△DEF,所以AB= DE,结论正
确:△ABC与△DEF关于直线MN成轴对称,则△ABC≌
△DEF,所以∠B= ∠E,结论正确.故选B.
D
A.如果图形甲和图形乙关于直线MN对称,则图形甲与
图形乙成轴对称,但图形甲不一定是轴对称图形,故A错误;
有些图形没有对称轴,故B错误;平面上两个大小、形状
完全一样的图形是全等形,但它们不一定成轴对称,故C错
误;如果△ABC和△EFC成轴对称,那么它们全等,故它们
的面积一定相等,故D正确.故选D.
二.
1.答案15
解析∵P点关于OA、OB的对称点是、,
∴PM =M,PN =N,
7.APMIV的躜长=PM+MN+PN=P、M+MN+N=,
∵△PMN的周长是15 cm.
∴= 15 Cm.故答案为15.
三
1.证明(1)∵GB=GC,AB=AC,
∴点G,点A在BC的垂直平分线上,
又∵两点确定一条直线.∴AG垂直平分BC.
(2)∵AG垂直平分BG,点D在AG上,
∴DB =DC.
2.解析如图(1),过BC,EF的交点交点和点A作直线,该直
线就是所求作的直线;如图(2),过BC,FE的延长线的交点
和AC,DE的延长线的交点作直线,该直线就是所求作的直
线.
13.1轴对称(2)答案:
一.
A 根据轴对称的性质可知,序号(1)对应的三角形与△ABC
的对应点所连的线段被一条直线(对称轴)垂直平分,故选A.
B ∵边AB与AD关于AC对称,
∴AC垂直平分BD.
∴CA平分∠BCD.AC乎分∠BAD,BD⊥AC.无法判断BD是否
平分AC.综上所述,结论正确的是①②③.
A
A中图形不是轴对称图形;B中图形是轴对称图形;C中
图形是轴对称图形;D中图形是轴对称图形.故选A.
C
∵△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE
=3 cm.∴BD =AD.AB= 2AE=6 cm.
∵△ADC的周长为9 cm.
∴ AC+AD+CD=AC+BD+CD =AC+BC=9 cm,
∴△ABC的周长为AB+AC+BC= 15 cm.故选C.
C
根据轴对称图形的概念,可知选项C中的图形不是轴对
称图形,故选C.
6.C该图形的对称轴是直线,故选C.
7. A
∵D为BC的中点,且BC=6,
∴BD=BC=3,由折叠性质知NA=ND,
则∠DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=9+3=12.故选A.
二
1.答案80°
解析∵直线m是多边形ABCDE的对称轴,∠A= 120°,∠B
=110°,∴ ∠E= ∠A= 120°,∠D=∠B=110°,
∴∠BCD= 540°-120°×2-110°x2= 80°.故答案为80°.
2.答案24
解析∵直线AD是△ABC的一条对称轴,
∴BD= CD=4 cm,AB=AC=8 cm,∴BC=BD+CD=8 cm,
∴△ABC的周长=AB+AC+BC= 24 cm.
3.答案16
解析∵DE是AB的垂直平分线,
∴AE=BE.
∵AC=10.曰C=6.
∴△BCE的周长=BC+BE+CE
=BC+AE+CE=BC+AC=6+10=16.
故答案为16.
三.
1.解析如图所示.
2.解析(1)如图,连接B'B",画线段B'B"的垂直平分线EF.则
直线EF即为所求.
(2)连接BO,B'O.B"O.
因为△ABC和△A'B'C'关于直线MN对称,
所以∠BOM=∠B'OM.
因为△A'B'C'和△A'B"C"关于直线EF对称,
所以∠B'OE= ∠B"OE.
所以∠BOB"= ∠BOM+∠B'OM+∠B'OE+∠B"OE=2( ∠B'OM
+∠B'OE)=2∠MOE.即∠BOB"= 2α.
一.选择
1.下列图形中,是轴对称图形的是 ( )
A B C D
2.如图13 -1-1所示的五角星是轴对称图形,它的对称轴共有 ( )
A.1条 B.3条 C.5条 D.无数条
3.如图13 -1-2.在△ABC中,BA=BC,∠ABC= 120°,AB的垂直平分线交AC于点M,交AB于点E,BC的垂直平分线交AC于点N,交BC于点F,连接BM,BN,若AC= 24,则△BMN的周长是( )
A.36 B.24 C.18 D.16
4.如图13 -1-3,在△ABC中,AB =AC= 20 cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35 cm,则BC的长为 ( )
A.5 cm B.10 cm C.15 cm D.17.5 cm
5.如图13 -1-4,在暑假期间,某学校对其校内的高中楼(图中的点A),临建楼(图中的点日)和图书馆(图中的点C)进行装修,装修工人小明需要放置一批装修物资,使得装修物资到点A.点召和点C的距离相等,则装修物资应该放置在 ( )
AC、BC两边高线的交点处
B.在AC、BC两边中线的交点处
C.在∠A、∠B两内角平分线的交点处
D.在AC、BC两边垂直平分线的交点处
6.如图13 -1-6,△ABC与△DEF关于直线MN成轴对称,则以下结论中不一定正确的是 ( )
A.A、D的连线被MN垂直平分 B.AB∥DF C.AB =DE D.∠B= ∠E
7.下列说法正确的是 ( )
A.如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形
B.任何一个图形都有对称轴,有的图形不止一条对称轴
C.平面上两个大小、形状完全一样的图形一定关于某直线对称
D.如果△ABC和△EFG成轴对称,那么它们的面积一定相等
二、填空
1.如图13 -1-10所示,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点,,连接交OA于M,交OB于N,连接PM,PN,若△PMN的周长为15 cm,则 = cm.
三.按要求做题
1.如图13 -1-5,在△ABC中.AB=AC,G为三角形外一点,且GB= GC.
(1)求证:AG垂直平分BC;
(2)点D在AG上,求证:DB =DC.
2.如图13 -1-7,△ABC与△DFE关于直线对称,请仅用无刻度的直尺,在图13-1-7(1)与图13-1-7(2)中分别作出直线.
13.1轴对称(2)
一.选择
1.图13 -1-8中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是 ( )
(1) B(2) C.(3) D.(4)
2.如图13 -1-9,在四边形ABCD中,边AB与AD关于AC对称,则下面结论正确的是 ( )
①CA平分∠BCD; ②AC平分∠BAD; ③BD⊥AC; ④BD平分AC.
①② B.①②③ C.②③④ D.①②③④
3.图书馆的标志是浓缩了图书馆文化的符号,下列图书馆标志中,不是轴对称图形的是 ( )
A B C D
4.如图13 -1-11,△ABC中边AB的垂直平分线分别交BC,AB于点D,E,AE=3 cm,△ADC的周长为9 cm,则△ABC的周长是( )
A.10 cm B.12 cm C.15 cm D.17 cm
5.下列图形中,不是轴对称图形的是 ( )
A B C D
6.图13 -1-14是由“○”和“□”组成的轴对称图形,该图形的对称轴是直线 ( )
B. C. D.
7.如图13 -1- 15,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为 ( )
A.12 B.13 C.14 D.15
二、填空
1.如图13 -1-12,直线m是多边形ABCDE的对称轴,其中∠A= 120°,∠B= 110°,那么∠BCD的度数为 .
2.如图13 -1- 13,直线AD是△ABC的一条对称轴,AC=8 cm,DC=4 cm,则△ABC的周长为 cm.
3.如图13 -1 - 16,在△ABC中,AC=10,BC=6,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是 .
三、按要求做题
1.请你用3种方法,将四块如图13 -1-17所示的小正方形纸板拼成一个大的正方形,并且使拼咸的大正方形是至少有两条对称轴的轴对称图形.
2.如图13 -1-18.已知△ABC和△A'B'C'关于直线MN对称,△A'B'C'和△A"B"C"关于直线EF对称.
(1)画出直线EF;
(2)若直线MN与EF相交于点O,试探究∠BOB"与直线MN、EF所夹角α的数量关系.
13.1轴对称(1)答案:
1.D选项A,B.C中的图形沿着某条直线折叠,直线两旁的部
分不能重合,所以选项A,B,C中的图形都不是轴对称图形,
故选D.
2.C五角星的对称轴共有5条,故选C.
3.B∵直线ME为线段AB的垂直平分线,
∴MA= MB,又直线NF为线段BC的垂直平分线,
∴NB =NC,∴△BMN的周长=BM+MN+BN =AM+MN+NC=AC= 24,故选B.
4.C∵DE垂直平分AB.∴AD=BD.
又∵△DBC的周长=BC+BD+CD=35 cm,
∴BC+AD+CD= 35 cm.
∵AC=AD+DC=20 cm,
∴BC= 35-20= 15 cm.故选C.
D
作AC、BC两边的垂直平分线,它们的交点是P,由线段的
垂直平分线的性质,知PA =PB =PC.故选D.
B
△ABC与△DEF关于直线MN成轴对稼,所以A、D的
连线被MN垂直平分,故结论正确;由已知条件无法判定
AB与DF平行,故结论不一定正确;△ABC与△DEF关于
直线MN成轴对称,则△ABC≌△DEF,所以AB= DE,结论正
确:△ABC与△DEF关于直线MN成轴对称,则△ABC≌
△DEF,所以∠B= ∠E,结论正确.故选B.
D
A.如果图形甲和图形乙关于直线MN对称,则图形甲与
图形乙成轴对称,但图形甲不一定是轴对称图形,故A错误;
有些图形没有对称轴,故B错误;平面上两个大小、形状
完全一样的图形是全等形,但它们不一定成轴对称,故C错
误;如果△ABC和△EFC成轴对称,那么它们全等,故它们
的面积一定相等,故D正确.故选D.
二.
1.答案15
解析∵P点关于OA、OB的对称点是、,
∴PM =M,PN =N,
7.APMIV的躜长=PM+MN+PN=P、M+MN+N=,
∵△PMN的周长是15 cm.
∴= 15 Cm.故答案为15.
三
1.证明(1)∵GB=GC,AB=AC,
∴点G,点A在BC的垂直平分线上,
又∵两点确定一条直线.∴AG垂直平分BC.
(2)∵AG垂直平分BG,点D在AG上,
∴DB =DC.
2.解析如图(1),过BC,EF的交点交点和点A作直线,该直
线就是所求作的直线;如图(2),过BC,FE的延长线的交点
和AC,DE的延长线的交点作直线,该直线就是所求作的直
线.
13.1轴对称(2)答案:
一.
A 根据轴对称的性质可知,序号(1)对应的三角形与△ABC
的对应点所连的线段被一条直线(对称轴)垂直平分,故选A.
B ∵边AB与AD关于AC对称,
∴AC垂直平分BD.
∴CA平分∠BCD.AC乎分∠BAD,BD⊥AC.无法判断BD是否
平分AC.综上所述,结论正确的是①②③.
A
A中图形不是轴对称图形;B中图形是轴对称图形;C中
图形是轴对称图形;D中图形是轴对称图形.故选A.
C
∵△ABC中,边AB的中垂线分别交BC、AB于点D、E,AE
=3 cm.∴BD =AD.AB= 2AE=6 cm.
∵△ADC的周长为9 cm.
∴ AC+AD+CD=AC+BD+CD =AC+BC=9 cm,
∴△ABC的周长为AB+AC+BC= 15 cm.故选C.
C
根据轴对称图形的概念,可知选项C中的图形不是轴对
称图形,故选C.
6.C该图形的对称轴是直线,故选C.
7. A
∵D为BC的中点,且BC=6,
∴BD=BC=3,由折叠性质知NA=ND,
则∠DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=9+3=12.故选A.
二
1.答案80°
解析∵直线m是多边形ABCDE的对称轴,∠A= 120°,∠B
=110°,∴ ∠E= ∠A= 120°,∠D=∠B=110°,
∴∠BCD= 540°-120°×2-110°x2= 80°.故答案为80°.
2.答案24
解析∵直线AD是△ABC的一条对称轴,
∴BD= CD=4 cm,AB=AC=8 cm,∴BC=BD+CD=8 cm,
∴△ABC的周长=AB+AC+BC= 24 cm.
3.答案16
解析∵DE是AB的垂直平分线,
∴AE=BE.
∵AC=10.曰C=6.
∴△BCE的周长=BC+BE+CE
=BC+AE+CE=BC+AC=6+10=16.
故答案为16.
三.
1.解析如图所示.
2.解析(1)如图,连接B'B",画线段B'B"的垂直平分线EF.则
直线EF即为所求.
(2)连接BO,B'O.B"O.
因为△ABC和△A'B'C'关于直线MN对称,
所以∠BOM=∠B'OM.
因为△A'B'C'和△A'B"C"关于直线EF对称,
所以∠B'OE= ∠B"OE.
所以∠BOB"= ∠BOM+∠B'OM+∠B'OE+∠B"OE=2( ∠B'OM
+∠B'OE)=2∠MOE.即∠BOB"= 2α.
