第五章 圆单元测试题A(含答案)
图片预览

文档简介
鲁教版五四制数学九年级第五单元测试题(A)
时间:60分钟 满分:100分
一、选择题(30分)
1.(眉山中考)如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连接BC,若∠P=36°,则∠B等于( )
A.27° B.32° C.36° D.54°
2.(聊城中考)如图,在⊙O中,弦BC与半径OA相交于点D,连接AB,OC。若∠OAB=60°,∠ADC=85°,则∠OCB的度数是( )
A.25° B.27.5° C.30° D.35°
3.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
4.(衢州中考)如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的侧面积为15πcm2,则sin∠ABC的值为( )
A. B. C. D.
5.如图,在Rt△ABC中,∠C=90°,∠B=30°,B=4cm,以点C为圆心,2cm长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
6.(烟台中考)如图,四边形ABCD内接于⊙O,点I是ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56° B.62° C.68° D.78°
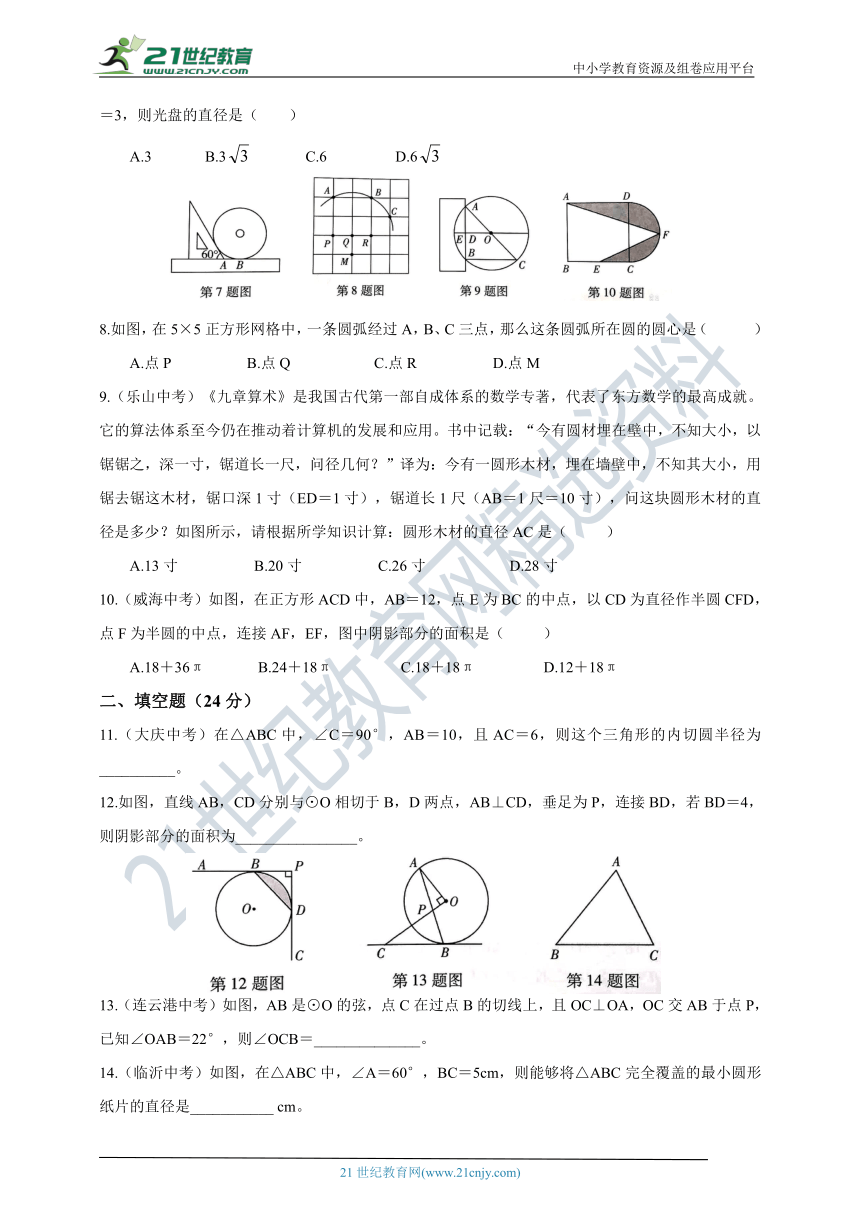
7.(深圳中考)如图,一把直尺、60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是( )
A.3 B.3 C.6 D.6
8.如图,在5×5正方形网格中,一条圆弧经过A,B、C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
9.(乐山中考)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就。它的算法体系至今仍在推动着计算机的发展和应用。书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:今有一圆形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆形木材的直径是多少?如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
10.(威海中考)如图,在正方形ACD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
二、填空题(24分)
11.(大庆中考)在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为__________。
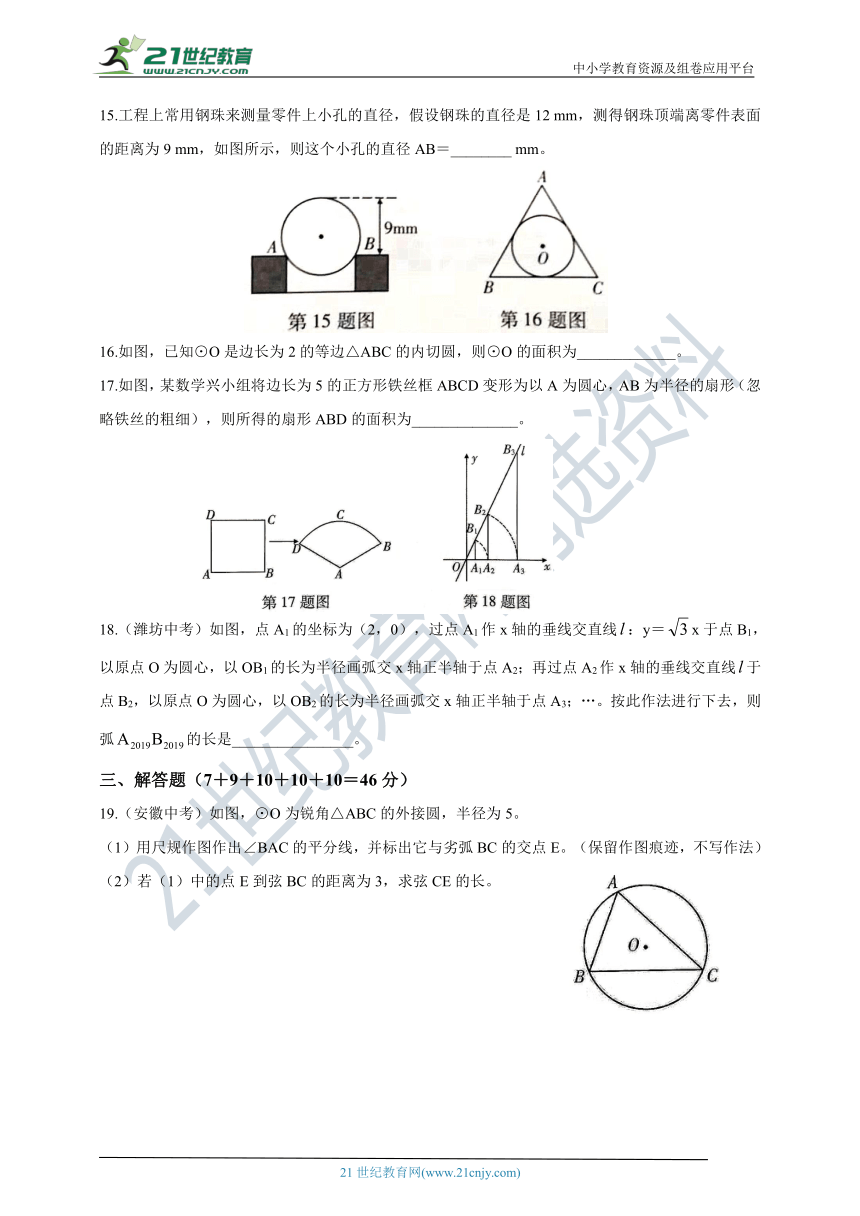
12.如图,直线AB,CD分别与⊙O相切于B,D两点,AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为________________。
13.(连云港中考)如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=______________。
14.(临沂中考)如图,在△ABC中,∠A=60°,BC=5cm,则能够将△ABC完全覆盖的最小圆形纸片的直径是___________ cm。
15.工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是12 mm,测得钢珠顶端离零件表面的距离为9 mm,如图所示,则这个小孔的直径AB=________ mm。
16.如图,已知⊙O是边长为2的等边△ABC的内切圆,则⊙O的面积为_____________。
17.如图,某数学兴小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为______________。
18.(潍坊中考)如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线:y=x于点B1,以原点O为圆心,以OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;…。按此作法进行下去,则弧的长是________________。
三、解答题(7+9+10+10+10=46分)
19.(安徽中考)如图,⊙O为锐角△ABC的外接圆,半径为5。
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E。(保留作图痕迹,不写作法)(2)若(1)中的点E到弦BC的距离为3,求弦CE的长。
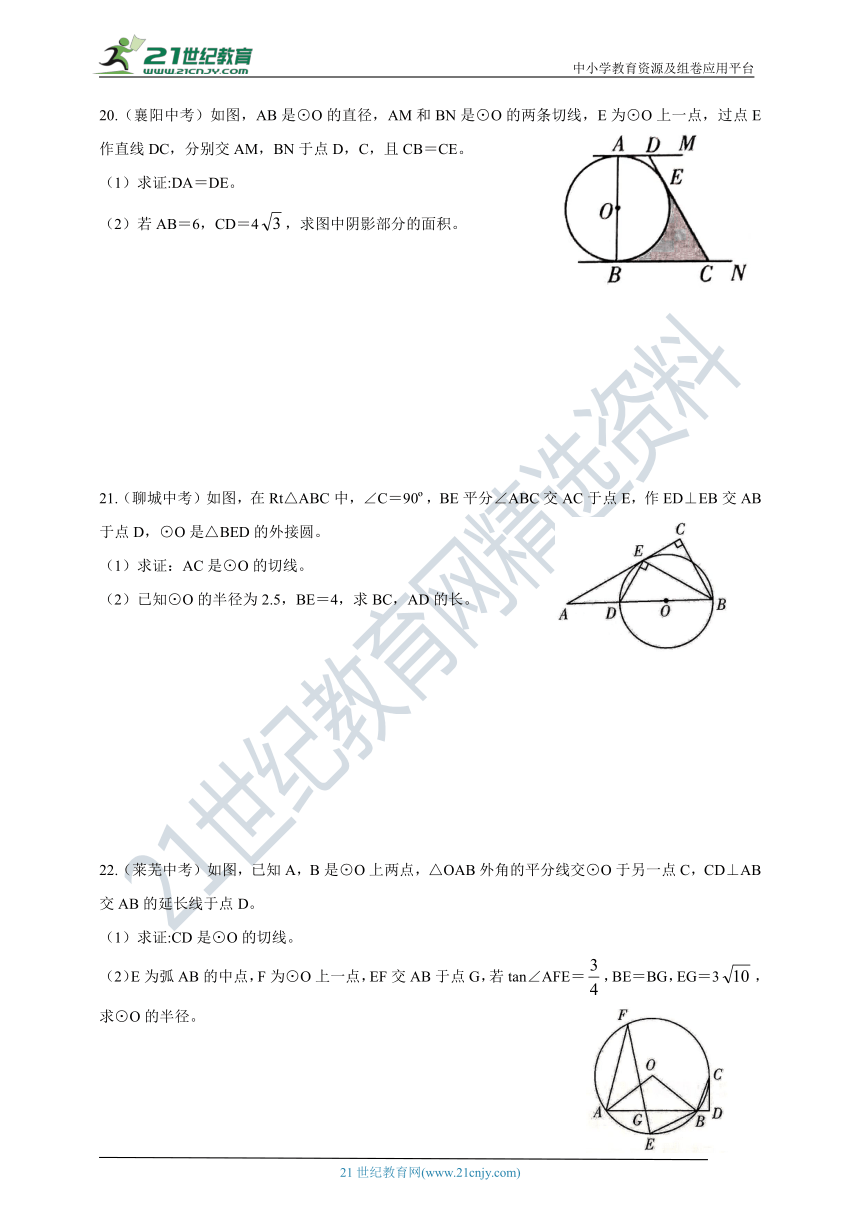
20.(襄阳中考)如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC,分别交AM,BN于点D,C,且CB=CE。
(1)求证:DA=DE。
(2)若AB=6,CD=4,求图中阴影部分的面积。
21.(聊城中考)如图,在Rt△ABC中,∠C=90o,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆。
(1)求证:AC是⊙O的切线。
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长。
22.(莱芜中考)如图,已知A,B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于点D。
(1)求证:CD是⊙O的切线。
(2)E为弧AB的中点,F为⊙O上一点,EF交AB于点G,若tan∠AFE=,BE=BG,EG=3,求⊙O的半径。
23.(威海中考)已知,AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F。
(1)如图①,若DE∥AB,求证:CF=EF。
(2)如图②,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由。
参考答案及解析
一、1. A 2.D 3.B 4.C 5. B 6.C 7. D 8.B 9.C 10. C
二、11.2 12.2π-4 13.440 14. 15.6 16.
17. 25 18.
三、19.解:(1)如图,AE即为所作。
(2)连接OE交BC于点F,连接DC。∵AE平分 ∠BAC,∴∠BAE=∠CAE。
∵弧BE=弧CE,∴DE ⊥BC,∴EF=3,∴OF=5-3=2。
在Rt△OCF中,CF=。在Rt△CEF中,CE=。
20.(1)证明:如图,连接OE,BE。∵OB=OE, ∴∠OBE=∠OEB。∵BC=EC,∴∠CBE=∠CEB,∴∠OBC=∠OEC。∵BC为⊙O的切线,∴∠OEC =∠OBC=90o。∵OE为⊙O的半径,∴CD为⊙O的切线。∵AD切⊙O于点A,∴DA=DE。
(2)解:如图,连接OC,过点D作DF⊥BC于点F,则四边形ABFD是矩形,∴ AD= BF,DF=AB=6,∴DC=EC+DE=BC+AD=4. ∵FC=,∴BC-AD =2,∴BC=3。在R t△OBC中, tan ∠BOC =,∴∠BOC=60o,在△OEC与△OBC中, . ∵,∴△OEC≌△OBC(SSS),∴∠ BOE=2 ∠BOC= 120o。
∴S阴影部分=S四边形BCEO-S扇形OBE=2 ×BC.OB-。
21. (1)证明:如图,连接OE. ∵OB=OE,∴∠OBE=∠OEB。∵ BE平分∠ABC, ∠OBE=∠ EBC,. ∴∠OEB =∠EBC,∴OE∥BC。又∵∠C=90o,∴∠OEA= 90o,即AC⊥OE。又∵DE是⊙O的半径,∴ AC是⊙O的切线。
(2)解:在△BCE与△BED中.∵∠C=∠BED=90o,∠EBC=∠DBE,∴△BCE∽△BED。
∴,即BC=。∵BE=4,BD是⊙O的直径,即BD=5,∴BC=。
又∵ OE∥BC。∴。∵AO=AD +2.5, AB=AD+5,
∴,解得AD=。
22. (1)证明:如图,连接OC,∵BC平分∠OBD,∴∠OBC= ∠CBD。
∵ OB=OC,∴∠OBC= ∠OCB,∴∠OCB= ∠CBD,∴OC∥AD。又∵CD⊥AB,∴OC⊥CD,. ∴CD是⊙O的切线。
(2)解:如图,连接OE交AB于点H。∵E为弧AB的中点,∴OE⊥AB。∴∠ABE=∠AFE,
∴tan∠ABE=tan ∠AFE=,∴ 在 Rt△BEH 中,tan∠HBE=,设EH=3x,则BH=4x,BE=5x,∴BC=BE=5x,∴GH= x。在Rt△EHC中,由勾股定理得x2+(3x)2=(3)2,解得x=3,∴EH=9,BH=12.设⊙O的半径为r,则OH=r-9.在Rt△OHB中,由勾股定理得(r-9)2+122=r2,解得r=,即⊙O的半径为。
23.(1)证明:如图①,连接OD,OE。∵AB=2,∴OA=OD=OE=OB=1。∵DE=1,∴OD=OE=DE,∴△ODE是等边三角形,∴∠ODE=∠OED=60°。∵DE∥AB,∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,∴△AOD和△BOE是等边三角形,∴∠OAD=∠OBE=60°。 ∵DE∥AB,∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,∴△CDE是等边三角形。∵DF是⊙O的切线,∴OD⊥DF,∴∠EDF=90°-60°=30°,∴∠DFE=90°,∴DF⊥CE,∴CF=EF。
(2)解:相等。理由:如图②,点E运动至与点B重合时,BC是⊙O的切线,∵⊙O的切线DF交BC于点F,∴BF=DF,∴∠BDF=∠DBF。∵AB是⊙O的直径,∴∠ADB=∠BDC=90°,∴∠FDC=∠C,∴DF=CF,∴BF=CF。
时间:60分钟 满分:100分
一、选择题(30分)
1.(眉山中考)如图所示,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C,连接BC,若∠P=36°,则∠B等于( )
A.27° B.32° C.36° D.54°
2.(聊城中考)如图,在⊙O中,弦BC与半径OA相交于点D,连接AB,OC。若∠OAB=60°,∠ADC=85°,则∠OCB的度数是( )
A.25° B.27.5° C.30° D.35°
3.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF等于( )
A.12.5° B.15° C.20° D.22.5°
4.(衢州中考)如图,AB是圆锥的母线,BC为底面直径,已知BC=6cm,圆锥的侧面积为15πcm2,则sin∠ABC的值为( )
A. B. C. D.
5.如图,在Rt△ABC中,∠C=90°,∠B=30°,B=4cm,以点C为圆心,2cm长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
6.(烟台中考)如图,四边形ABCD内接于⊙O,点I是ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56° B.62° C.68° D.78°
7.(深圳中考)如图,一把直尺、60°的直角三角板和光盘如图摆放,A为60°角与直尺交点,AB=3,则光盘的直径是( )
A.3 B.3 C.6 D.6
8.如图,在5×5正方形网格中,一条圆弧经过A,B、C三点,那么这条圆弧所在圆的圆心是( )
A.点P B.点Q C.点R D.点M
9.(乐山中考)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就。它的算法体系至今仍在推动着计算机的发展和应用。书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:今有一圆形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆形木材的直径是多少?如图所示,请根据所学知识计算:圆形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
10.(威海中考)如图,在正方形ACD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
二、填空题(24分)
11.(大庆中考)在△ABC中,∠C=90°,AB=10,且AC=6,则这个三角形的内切圆半径为__________。
12.如图,直线AB,CD分别与⊙O相切于B,D两点,AB⊥CD,垂足为P,连接BD,若BD=4,则阴影部分的面积为________________。
13.(连云港中考)如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=______________。
14.(临沂中考)如图,在△ABC中,∠A=60°,BC=5cm,则能够将△ABC完全覆盖的最小圆形纸片的直径是___________ cm。
15.工程上常用钢珠来测量零件上小孔的直径,假设钢珠的直径是12 mm,测得钢珠顶端离零件表面的距离为9 mm,如图所示,则这个小孔的直径AB=________ mm。
16.如图,已知⊙O是边长为2的等边△ABC的内切圆,则⊙O的面积为_____________。
17.如图,某数学兴小组将边长为5的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形ABD的面积为______________。
18.(潍坊中考)如图,点A1的坐标为(2,0),过点A1作x轴的垂线交直线:y=x于点B1,以原点O为圆心,以OB1的长为半径画弧交x轴正半轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,以OB2的长为半径画弧交x轴正半轴于点A3;…。按此作法进行下去,则弧的长是________________。
三、解答题(7+9+10+10+10=46分)
19.(安徽中考)如图,⊙O为锐角△ABC的外接圆,半径为5。
(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧BC的交点E。(保留作图痕迹,不写作法)(2)若(1)中的点E到弦BC的距离为3,求弦CE的长。
20.(襄阳中考)如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC,分别交AM,BN于点D,C,且CB=CE。
(1)求证:DA=DE。
(2)若AB=6,CD=4,求图中阴影部分的面积。
21.(聊城中考)如图,在Rt△ABC中,∠C=90o,BE平分∠ABC交AC于点E,作ED⊥EB交AB于点D,⊙O是△BED的外接圆。
(1)求证:AC是⊙O的切线。
(2)已知⊙O的半径为2.5,BE=4,求BC,AD的长。
22.(莱芜中考)如图,已知A,B是⊙O上两点,△OAB外角的平分线交⊙O于另一点C,CD⊥AB交AB的延长线于点D。
(1)求证:CD是⊙O的切线。
(2)E为弧AB的中点,F为⊙O上一点,EF交AB于点G,若tan∠AFE=,BE=BG,EG=3,求⊙O的半径。
23.(威海中考)已知,AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F。
(1)如图①,若DE∥AB,求证:CF=EF。
(2)如图②,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由。
参考答案及解析
一、1. A 2.D 3.B 4.C 5. B 6.C 7. D 8.B 9.C 10. C
二、11.2 12.2π-4 13.440 14. 15.6 16.
17. 25 18.
三、19.解:(1)如图,AE即为所作。
(2)连接OE交BC于点F,连接DC。∵AE平分 ∠BAC,∴∠BAE=∠CAE。
∵弧BE=弧CE,∴DE ⊥BC,∴EF=3,∴OF=5-3=2。
在Rt△OCF中,CF=。在Rt△CEF中,CE=。
20.(1)证明:如图,连接OE,BE。∵OB=OE, ∴∠OBE=∠OEB。∵BC=EC,∴∠CBE=∠CEB,∴∠OBC=∠OEC。∵BC为⊙O的切线,∴∠OEC =∠OBC=90o。∵OE为⊙O的半径,∴CD为⊙O的切线。∵AD切⊙O于点A,∴DA=DE。
(2)解:如图,连接OC,过点D作DF⊥BC于点F,则四边形ABFD是矩形,∴ AD= BF,DF=AB=6,∴DC=EC+DE=BC+AD=4. ∵FC=,∴BC-AD =2,∴BC=3。在R t△OBC中, tan ∠BOC =,∴∠BOC=60o,在△OEC与△OBC中, . ∵,∴△OEC≌△OBC(SSS),∴∠ BOE=2 ∠BOC= 120o。
∴S阴影部分=S四边形BCEO-S扇形OBE=2 ×BC.OB-。
21. (1)证明:如图,连接OE. ∵OB=OE,∴∠OBE=∠OEB。∵ BE平分∠ABC, ∠OBE=∠ EBC,. ∴∠OEB =∠EBC,∴OE∥BC。又∵∠C=90o,∴∠OEA= 90o,即AC⊥OE。又∵DE是⊙O的半径,∴ AC是⊙O的切线。
(2)解:在△BCE与△BED中.∵∠C=∠BED=90o,∠EBC=∠DBE,∴△BCE∽△BED。
∴,即BC=。∵BE=4,BD是⊙O的直径,即BD=5,∴BC=。
又∵ OE∥BC。∴。∵AO=AD +2.5, AB=AD+5,
∴,解得AD=。
22. (1)证明:如图,连接OC,∵BC平分∠OBD,∴∠OBC= ∠CBD。
∵ OB=OC,∴∠OBC= ∠OCB,∴∠OCB= ∠CBD,∴OC∥AD。又∵CD⊥AB,∴OC⊥CD,. ∴CD是⊙O的切线。
(2)解:如图,连接OE交AB于点H。∵E为弧AB的中点,∴OE⊥AB。∴∠ABE=∠AFE,
∴tan∠ABE=tan ∠AFE=,∴ 在 Rt△BEH 中,tan∠HBE=,设EH=3x,则BH=4x,BE=5x,∴BC=BE=5x,∴GH= x。在Rt△EHC中,由勾股定理得x2+(3x)2=(3)2,解得x=3,∴EH=9,BH=12.设⊙O的半径为r,则OH=r-9.在Rt△OHB中,由勾股定理得(r-9)2+122=r2,解得r=,即⊙O的半径为。
23.(1)证明:如图①,连接OD,OE。∵AB=2,∴OA=OD=OE=OB=1。∵DE=1,∴OD=OE=DE,∴△ODE是等边三角形,∴∠ODE=∠OED=60°。∵DE∥AB,∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,∴△AOD和△BOE是等边三角形,∴∠OAD=∠OBE=60°。 ∵DE∥AB,∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,∴△CDE是等边三角形。∵DF是⊙O的切线,∴OD⊥DF,∴∠EDF=90°-60°=30°,∴∠DFE=90°,∴DF⊥CE,∴CF=EF。
(2)解:相等。理由:如图②,点E运动至与点B重合时,BC是⊙O的切线,∵⊙O的切线DF交BC于点F,∴BF=DF,∴∠BDF=∠DBF。∵AB是⊙O的直径,∴∠ADB=∠BDC=90°,∴∠FDC=∠C,∴DF=CF,∴BF=CF。
