六年级上册数学一课一练-4.2问题解决(含答案)
文档属性
| 名称 | 六年级上册数学一课一练-4.2问题解决(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 59.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-21 21:50:43 | ||
图片预览


文档简介
六年级上册数学一课一练-4.2问题解决
一、单选题
1.10克糖放入100克水中。糖与糖水的质量比是(?? )。
A.?1:10?????????????????????????????????????????B.?10:1?????????????????????????????????????????C.?1:11
2.从甲盐库取出 的盐运到乙盐库,这时两个盐库所存的盐的质量相等,原来甲盐库和乙盐库的存盐质量的比是多少?(??? )
A.?5:3????????????????????????????????????????B.?4:5????????????????????????????????????????C.?6:5????????????????????????????????????????D.?5:4
3.比例尺是(? )
A.?一个比例???????????????????????????????????B.?一个比???????????????????????????????????C.?一个方程
4.在一个圆里面做一个最大的正方形,正方形和圆的面积比是(? )。
A.?4:π???????????????????????????????????B.?2:π???????????????????????????????????C.?π:2???????????????????????????????????D.?π:4
二、判断题
5.判断,正确的填“正确”,错误的填“错误”.明和哥哥去年的年龄比是5∶8,今年他们的年龄比不变。
6.甲数比乙数少 ,甲数和乙数的比是5:2.。
7.一块长方形菜地有984平方米,计划按3:5种茄子和西红柿,茄子要种369平方米。
三、填空题
8.种植50棵树,成活了47棵.成活棵树与总棵树的比是________∶________,化成后项是100的比是________∶________.
9.甲、乙两人每天加工零件个数的比是3:4,两人合作15天后,甲、乙两人各自加工零件的个数比是________。
10.鸡只数的 等于鸭只数的 ,则鸡只数与鸭只数的比是________∶________.
11.六(1)班人数在40到50之间,如果男生和女生的人数比是6∶5,这个班有________人.
四、解答题
12.我们共植树800棵,没有成活的有12棵。写出植树总棵数与活了的棵数的比,并化简。
五、综合题
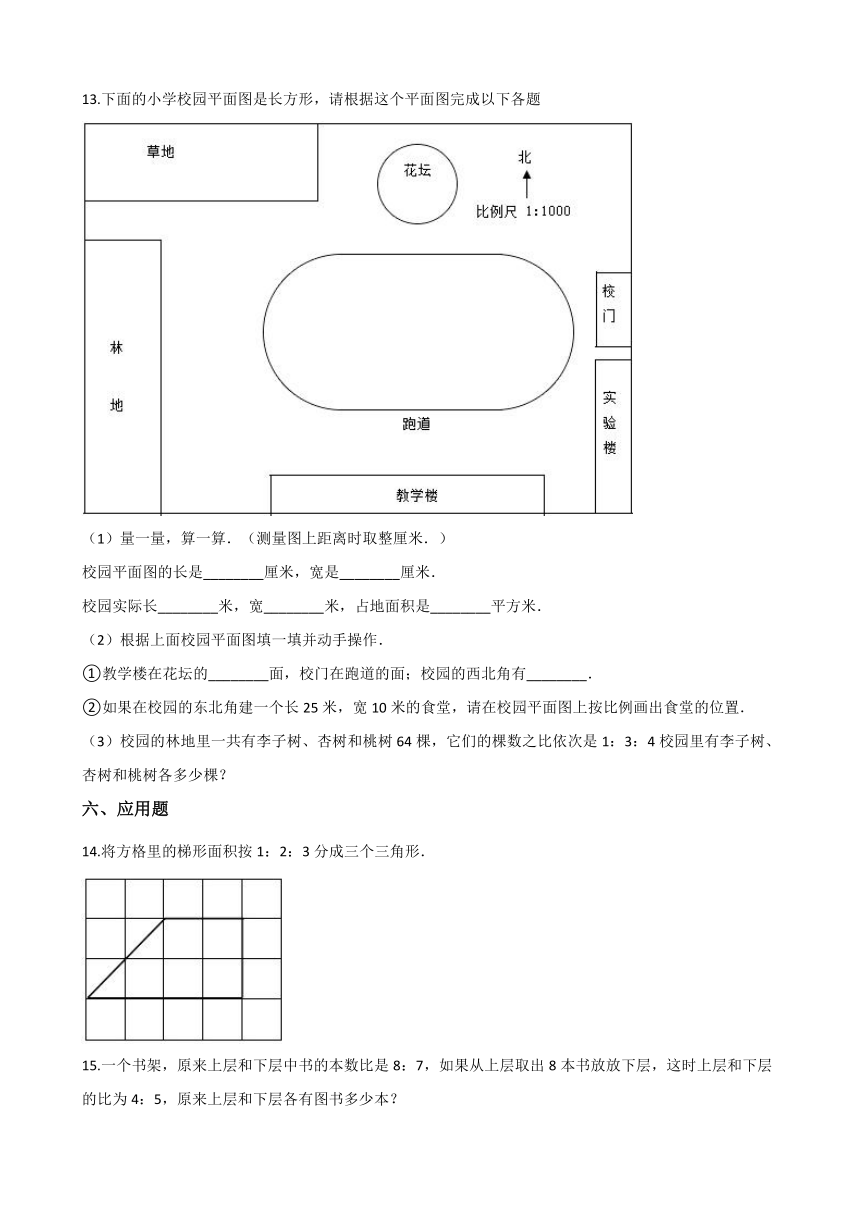
13.下面的小学校园平面图是长方形,请根据这个平面图完成以下各题
(1)量一量,算一算.(测量图上距离时取整厘米.)
校园平面图的长是________厘米,宽是________厘米.
校园实际长________米,宽________米,占地面积是________平方米.
(2)根据上面校园平面图填一填并动手操作.
①教学楼在花坛的________面,校门在跑道的面;校园的西北角有________.
②如果在校园的东北角建一个长25米,宽10米的食堂,请在校园平面图上按比例画出食堂的位置.
(3)校园的林地里一共有李子树、杏树和桃树64棵,它们的棵数之比依次是1:3:4校园里有李子树、杏树和桃树各多少棵?
六、应用题
14.将方格里的梯形面积按1:2:3分成三个三角形.
15.一个书架,原来上层和下层中书的本数比是8:7,如果从上层取出8本书放放下层,这时上层和下层的比为4:5,原来上层和下层各有图书多少本?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】糖:糖水=10:(10+100)=10:110=(10÷10):(110÷10)=1:11 故答案为:C.
【分析】根据题意可知,先求出糖水的质量,用糖的质量+水的质量=糖水的质量,然后用糖的质量:糖水的质量,按照化简整数比的方法:比的前项和后项同时除以前项和后项的最大公因数,可以化简比,据此解答.
2.【答案】 A
【解析】【解答】1:(1--)=5:3. 故答案为:A
【分析】,把甲盐库盐的质量看做单位“1,”根据题意可知,A乙盐库的盐的质量是甲盐库演的质量的(1--), 根据球两个数的比的方法即可得到答案。
3.【答案】 B
【解析】【解答】比例尺是图上距离与实际距离的比,所以比例尺以一个比。
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
故选:B
4.【答案】 B
【解析】【解答】解:假设圆的半径是1,则正方形和圆的面积比是: (1×1÷2×4):(π×12)=2:π 故答案为:B
【分析】画出正方形内的两条对角线,把这个正方形平均分成了4个等腰直角三角形,每个三角形直角边的长度与圆的半径相等,四个三角形的面积之和就是正方形的面积,假设圆的半径是1,写出正方形的面积与圆的面积比后化成最简整数比即可.
二、判断题
5.【答案】 错误
【解析】【解答】设他们去年年龄分别是:5岁、8岁
则今年的年龄比为:6:9≠5:8
所以错误
6.【答案】 错误
【解析】【解答】 ,因此本题是错误的,故本题的答案是错误 。
【分析】通过审题,根据甲数比乙数少 ,可以把乙数看成单位“1”,则甲数就是 ,然后根据比的意义列式即可解答.
7.【答案】 正确
【解析】【解答】解:984÷(3+5)=123(平方米),123×3=369(平方米)。 ?故答案为:正确。
【分析】总数÷总份数=每份数。再用每份数乘对应的份数得到对应的结果。
三、填空题
8.【答案】47;50;94;100
【解析】【解答】成活棵数与总棵数的比是:47:50,化成后项是100的比是:47:50=(47×2):(50×2)=94:100. 故答案为:47;50;94;100 【分析】写出成活棵数与总棵数的比,不要把前项与后项写反了;把比的前项和后项同时乘2即可化成后项是100的比.
9.【答案】3:4
【解析】【解答】解:合作15天后,甲、乙两人各自加工零件的个数比是3:4。 故答案为:3:4 【分析】由于两人工作的时间是相同的,那么两人加工的零件的个数比与每天加工零件的个数比是相同的。
10.【答案】 7;5
【解析】【解答】鸡的只数与鸭只数的比是:. 故答案为:7;5
【分析】等量关系:鸡的只数×=鸭的只数×, 根据等量关系写出只数比并化成最简整数比;也可以把假设鸡的只数是7,则鸭的只数是5,再写出比.
11.【答案】 44
【解析】【解答】6+5=11,则人数可能是11人、11×2=22(人),11×3=33(人),11×4=44(人)……,因为人数在40到50之间,那么这个班有44人. 故答案为:44
【分析】先算出男生和女生人数的份数和,那么总人数一定是份数和的倍数,找出40到50之间份数和的倍数即可判断出总人数.
四、解答题
12.【答案】解:800-12=788(棵),800:788=200:197
【解析】【分析】用植树总数减去没有成活的棵数求出成活的棵数,写出总棵数与成活的棵数比,把前项和后项同时除以4即可化成最简整数比。
五、综合题
13.【答案】 (1)12 ;8 ;120 ;80 ;9600
(2)南|东|草地 ;25米=2500厘米,10米=1000厘米,
则2500× =2.5厘米,1000× =1厘米,
所以食堂的位置如下图所示:
(3)解:64× =8(棵),
64× =24(棵),
64﹣8﹣24=32(棵);
答:校园里有李子树8棵、杏树24棵和桃树32棵.
【解析】【解答】解:(1)量得校园平面图的长是12厘米,宽是8厘米.
12÷ =12000(厘米)=120(米),
8÷ =8000(厘米)=80(米),
120×80=9600(平方米);
答:校园实际长120米,宽80米,占地面积是9600平方米.
(2)①教学楼在花坛的南面,校门在跑道的东面;校园的西北角有草地.
②25米=2500厘米,10米=1000厘米,
则2500× =2.5厘米,1000× =1厘米,
所以食堂的位置如下图所示:
【分析】(1)用直尺即可直接测量所需要的数据;再据“实际距离=图上距离÷比例尺”即可分别求出长和宽的实际长度,进而利用长方形的面积公式即可求解;(2)依据地图上的方向辨别方法,即“上北下南,左西右东”以及图上标注的其他信息,即可解答;先依据“图上距离=实际距离×比例尺”分别求出食堂的图上距离,进而完成画图;(3)果树的棵数比已知,于是可以求出总份数,进而利用按比例分配的方法即可得解.此题是一道综合性的题目,涉及到了比例尺的应用,地图上的方向辨别方法,以及按比例分配的方法,要求学生要细心审题,仔细作答.
六、应用题
14.【答案】 解:根据题干分析,可将这个梯形划分为如图所示的三个三角形,使它们的面积之比为1:2:3,
.
【解析】【分析】根据高一定时,三角形的面积与底成正比的关系,把三角形的高定为梯形的高,底按照1:2:3进行划分即可解答.此题考查了高一定时,三角形的面积与高成正比关系的灵活应用.
15.【答案】解:8÷( ﹣ ) =8÷( ﹣ ), =8÷ , =90(本); 则原来上层有书:90× =48(本); 下层有书:90× =42(本). 答:原来上层有书48本,下层有书42本.
【解析】【分析】在这一过程中,不变量是上下两层书的总本数,原来上层和下层中书的本数比是8:7,则原来上层书本数占总本数的 ,从上层取出8本书放放下层,这时上层和下层的比为4:5,则此时上层书的本数占总本数的 ,由此可得总本数为:8÷( ﹣ ),求出总本数后即能求出原来上层和下层各有图书多少本.根据前后上下两层本数比的变化求出前后两层本数占总本数分率的变化是完成本题的关健.
一、单选题
1.10克糖放入100克水中。糖与糖水的质量比是(?? )。
A.?1:10?????????????????????????????????????????B.?10:1?????????????????????????????????????????C.?1:11
2.从甲盐库取出 的盐运到乙盐库,这时两个盐库所存的盐的质量相等,原来甲盐库和乙盐库的存盐质量的比是多少?(??? )
A.?5:3????????????????????????????????????????B.?4:5????????????????????????????????????????C.?6:5????????????????????????????????????????D.?5:4
3.比例尺是(? )
A.?一个比例???????????????????????????????????B.?一个比???????????????????????????????????C.?一个方程
4.在一个圆里面做一个最大的正方形,正方形和圆的面积比是(? )。
A.?4:π???????????????????????????????????B.?2:π???????????????????????????????????C.?π:2???????????????????????????????????D.?π:4
二、判断题
5.判断,正确的填“正确”,错误的填“错误”.明和哥哥去年的年龄比是5∶8,今年他们的年龄比不变。
6.甲数比乙数少 ,甲数和乙数的比是5:2.。
7.一块长方形菜地有984平方米,计划按3:5种茄子和西红柿,茄子要种369平方米。
三、填空题
8.种植50棵树,成活了47棵.成活棵树与总棵树的比是________∶________,化成后项是100的比是________∶________.
9.甲、乙两人每天加工零件个数的比是3:4,两人合作15天后,甲、乙两人各自加工零件的个数比是________。
10.鸡只数的 等于鸭只数的 ,则鸡只数与鸭只数的比是________∶________.
11.六(1)班人数在40到50之间,如果男生和女生的人数比是6∶5,这个班有________人.
四、解答题
12.我们共植树800棵,没有成活的有12棵。写出植树总棵数与活了的棵数的比,并化简。
五、综合题
13.下面的小学校园平面图是长方形,请根据这个平面图完成以下各题
(1)量一量,算一算.(测量图上距离时取整厘米.)
校园平面图的长是________厘米,宽是________厘米.
校园实际长________米,宽________米,占地面积是________平方米.
(2)根据上面校园平面图填一填并动手操作.
①教学楼在花坛的________面,校门在跑道的面;校园的西北角有________.
②如果在校园的东北角建一个长25米,宽10米的食堂,请在校园平面图上按比例画出食堂的位置.
(3)校园的林地里一共有李子树、杏树和桃树64棵,它们的棵数之比依次是1:3:4校园里有李子树、杏树和桃树各多少棵?
六、应用题
14.将方格里的梯形面积按1:2:3分成三个三角形.
15.一个书架,原来上层和下层中书的本数比是8:7,如果从上层取出8本书放放下层,这时上层和下层的比为4:5,原来上层和下层各有图书多少本?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】糖:糖水=10:(10+100)=10:110=(10÷10):(110÷10)=1:11 故答案为:C.
【分析】根据题意可知,先求出糖水的质量,用糖的质量+水的质量=糖水的质量,然后用糖的质量:糖水的质量,按照化简整数比的方法:比的前项和后项同时除以前项和后项的最大公因数,可以化简比,据此解答.
2.【答案】 A
【解析】【解答】1:(1--)=5:3. 故答案为:A
【分析】,把甲盐库盐的质量看做单位“1,”根据题意可知,A乙盐库的盐的质量是甲盐库演的质量的(1--), 根据球两个数的比的方法即可得到答案。
3.【答案】 B
【解析】【解答】比例尺是图上距离与实际距离的比,所以比例尺以一个比。
【分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
故选:B
4.【答案】 B
【解析】【解答】解:假设圆的半径是1,则正方形和圆的面积比是: (1×1÷2×4):(π×12)=2:π 故答案为:B
【分析】画出正方形内的两条对角线,把这个正方形平均分成了4个等腰直角三角形,每个三角形直角边的长度与圆的半径相等,四个三角形的面积之和就是正方形的面积,假设圆的半径是1,写出正方形的面积与圆的面积比后化成最简整数比即可.
二、判断题
5.【答案】 错误
【解析】【解答】设他们去年年龄分别是:5岁、8岁
则今年的年龄比为:6:9≠5:8
所以错误
6.【答案】 错误
【解析】【解答】 ,因此本题是错误的,故本题的答案是错误 。
【分析】通过审题,根据甲数比乙数少 ,可以把乙数看成单位“1”,则甲数就是 ,然后根据比的意义列式即可解答.
7.【答案】 正确
【解析】【解答】解:984÷(3+5)=123(平方米),123×3=369(平方米)。 ?故答案为:正确。
【分析】总数÷总份数=每份数。再用每份数乘对应的份数得到对应的结果。
三、填空题
8.【答案】47;50;94;100
【解析】【解答】成活棵数与总棵数的比是:47:50,化成后项是100的比是:47:50=(47×2):(50×2)=94:100. 故答案为:47;50;94;100 【分析】写出成活棵数与总棵数的比,不要把前项与后项写反了;把比的前项和后项同时乘2即可化成后项是100的比.
9.【答案】3:4
【解析】【解答】解:合作15天后,甲、乙两人各自加工零件的个数比是3:4。 故答案为:3:4 【分析】由于两人工作的时间是相同的,那么两人加工的零件的个数比与每天加工零件的个数比是相同的。
10.【答案】 7;5
【解析】【解答】鸡的只数与鸭只数的比是:. 故答案为:7;5
【分析】等量关系:鸡的只数×=鸭的只数×, 根据等量关系写出只数比并化成最简整数比;也可以把假设鸡的只数是7,则鸭的只数是5,再写出比.
11.【答案】 44
【解析】【解答】6+5=11,则人数可能是11人、11×2=22(人),11×3=33(人),11×4=44(人)……,因为人数在40到50之间,那么这个班有44人. 故答案为:44
【分析】先算出男生和女生人数的份数和,那么总人数一定是份数和的倍数,找出40到50之间份数和的倍数即可判断出总人数.
四、解答题
12.【答案】解:800-12=788(棵),800:788=200:197
【解析】【分析】用植树总数减去没有成活的棵数求出成活的棵数,写出总棵数与成活的棵数比,把前项和后项同时除以4即可化成最简整数比。
五、综合题
13.【答案】 (1)12 ;8 ;120 ;80 ;9600
(2)南|东|草地 ;25米=2500厘米,10米=1000厘米,
则2500× =2.5厘米,1000× =1厘米,
所以食堂的位置如下图所示:
(3)解:64× =8(棵),
64× =24(棵),
64﹣8﹣24=32(棵);
答:校园里有李子树8棵、杏树24棵和桃树32棵.
【解析】【解答】解:(1)量得校园平面图的长是12厘米,宽是8厘米.
12÷ =12000(厘米)=120(米),
8÷ =8000(厘米)=80(米),
120×80=9600(平方米);
答:校园实际长120米,宽80米,占地面积是9600平方米.
(2)①教学楼在花坛的南面,校门在跑道的东面;校园的西北角有草地.
②25米=2500厘米,10米=1000厘米,
则2500× =2.5厘米,1000× =1厘米,
所以食堂的位置如下图所示:
【分析】(1)用直尺即可直接测量所需要的数据;再据“实际距离=图上距离÷比例尺”即可分别求出长和宽的实际长度,进而利用长方形的面积公式即可求解;(2)依据地图上的方向辨别方法,即“上北下南,左西右东”以及图上标注的其他信息,即可解答;先依据“图上距离=实际距离×比例尺”分别求出食堂的图上距离,进而完成画图;(3)果树的棵数比已知,于是可以求出总份数,进而利用按比例分配的方法即可得解.此题是一道综合性的题目,涉及到了比例尺的应用,地图上的方向辨别方法,以及按比例分配的方法,要求学生要细心审题,仔细作答.
六、应用题
14.【答案】 解:根据题干分析,可将这个梯形划分为如图所示的三个三角形,使它们的面积之比为1:2:3,
.
【解析】【分析】根据高一定时,三角形的面积与底成正比的关系,把三角形的高定为梯形的高,底按照1:2:3进行划分即可解答.此题考查了高一定时,三角形的面积与高成正比关系的灵活应用.
15.【答案】解:8÷( ﹣ ) =8÷( ﹣ ), =8÷ , =90(本); 则原来上层有书:90× =48(本); 下层有书:90× =42(本). 答:原来上层有书48本,下层有书42本.
【解析】【分析】在这一过程中,不变量是上下两层书的总本数,原来上层和下层中书的本数比是8:7,则原来上层书本数占总本数的 ,从上层取出8本书放放下层,这时上层和下层的比为4:5,则此时上层书的本数占总本数的 ,由此可得总本数为:8÷( ﹣ ),求出总本数后即能求出原来上层和下层各有图书多少本.根据前后上下两层本数比的变化求出前后两层本数占总本数分率的变化是完成本题的关健.
