冀教版数学六年级下册4.2《圆柱的表面积》一课一练(含答案)
文档属性
| 名称 | 冀教版数学六年级下册4.2《圆柱的表面积》一课一练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 92.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 08:00:40 | ||
图片预览

文档简介
《圆柱的表面积》习题
一、选择。
(1)圆柱底面半径扩大到原来3倍,高不变,圆柱侧面积扩大到原来( )倍。
A.3 B.9 C.6
(2)一个圆柱的高是12.56 cm,它的侧面展开后是一个正方形,这个圆柱的底面直径是( )cm。
A.12.56 B.4 C.2
(3)圆柱的底面半径不变,高缩小为原来的,圆柱的侧面积( )。
A.缩小为原来的 B.缩小为原来的 C.不变
(4)一个圆柱的侧面展开后是正方形,这个圆柱的高和底面直径的比是( )
A.π∶1 B.1∶π C.1∶1
二、认真判断。
1.一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体。 ( )
2.圆柱只有从上底面圆心到下底面圆心一条高。( )
3.圆柱体的表面积=底面积×2+底面积×高。( )
4.把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底那么制作的圆柱的高、侧面积、表面积一定相等。 ( )
5.侧面积相等的两个圆柱体,表面积也相等。( )
三、求下面圆柱的侧面积。
(1)底面周长为2.5 dm,高1.2 dm。
(2)底面直径为6 cm,高15 cm。
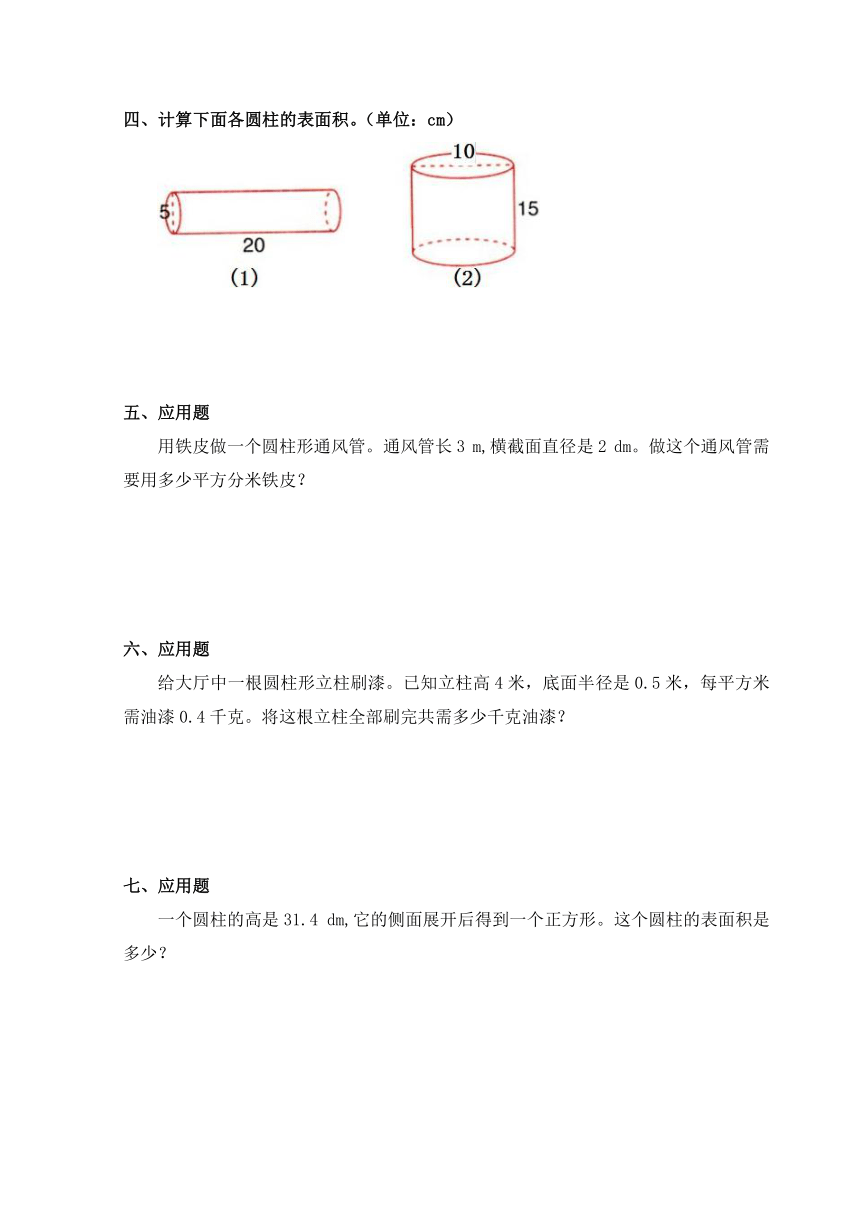
四、计算下面各圆柱的表面积。(单位:cm)
五、应用题
用铁皮做一个圆柱形通风管。通风管长3 m,横截面直径是2 dm。做这个通风管需要用多少平方分米铁皮?
六、应用题
给大厅中一根圆柱形立柱刷漆。已知立柱高4米,底面半径是0.5米,每平方米需油漆0.4千克。将这根立柱全部刷完共需多少千克油漆?
七、应用题
一个圆柱的高是31.4 dm,它的侧面展开后得到一个正方形。这个圆柱的表面积是多少?
八、应用题
如图,一个圆柱体被截去5 cm后,圆柱的表面积减少了31.4 cm2。求原来圆柱体的表面积是多少平方厘米?
(单位:cm)
九、应用题
下面是一张长方形纸板,按图示剪下阴影部分刚好能做成一个圆柱体。求做成的圆柱体的表面积。
十、应用题
如下图,高都是10厘米,底面半径分别是3厘米、6厘米的两个圆柱组成了一个几何体。求这个物体的表面积。
答案
一、(1)A (2)B (3)A (4)A
二、1.× 2.× 3.× 4.× 5.×
三、(1)2.5×1.2=3(dm2)
(2)3.14×6×15=282.6(cm2)
四、(1)侧面面积:3.14×5×20=314(cm2)
底面面积:2×3.14×(5÷2)2=39.25(cm2)
表面积:314+39.25=353.25(cm2)
(2)侧面面积:3.14×10×15=471(cm2)
底面面积:2×3.14×(10÷2)2=157(cm2)
表面积:471+157=628(cm2)
五、3m=30dm
3.14×2×30=188.4(平方分米)
六、2×3.14×0.5×4×0.4=5.024(千克)
七、31.4×31.4+3.14×(31.4÷3.14÷2)2×2=1142.96(dm2)
(分析:此圆柱的侧面展开的长方形的宽为圆柱的高即:31.4 dm,又因为是正方形,所以长也是31.4 dm,侧面展开面积可求,同时底面的周长也可知是31.4 dm,从而本可解。)
八、3.14×(31.4÷5÷3.14÷2)2×2+31.4÷5×20=131.88(平方厘米)
(分析:此题关键在于明白少的31.4 平方厘米是截去部分圆柱的侧面面积,与上底面面积无关。)
九、圆柱的底面直径:41.12÷(3.14+1+1)=8(cm)
圆柱的底面周长:41.12-8×2=25.12(cm)
圆柱的表面积:25.12×8+3.14×()2×2=301.44(cm2)
(分析:侧面展开图的长方形的长等于3.14个直径,而两个底面分别为一个直径,所以,本题中41.12 cm为(3.14+1+1)个直径,从而本题可解.)
十、物体表面积=大圆柱的表面积+小圆柱的侧面积=3.14×6×2×10+3.14×62×2+3.14×3×2×10=791.28(平方厘米)
(分析:本题关键在于两个圆柱的接合面面积不能加到表面积中,简易做法是:将小圆柱的上底面下移到大圆柱上,从面变为大圆柱的表面积与小圆柱侧面面积的和。)
一、选择。
(1)圆柱底面半径扩大到原来3倍,高不变,圆柱侧面积扩大到原来( )倍。
A.3 B.9 C.6
(2)一个圆柱的高是12.56 cm,它的侧面展开后是一个正方形,这个圆柱的底面直径是( )cm。
A.12.56 B.4 C.2
(3)圆柱的底面半径不变,高缩小为原来的,圆柱的侧面积( )。
A.缩小为原来的 B.缩小为原来的 C.不变
(4)一个圆柱的侧面展开后是正方形,这个圆柱的高和底面直径的比是( )
A.π∶1 B.1∶π C.1∶1
二、认真判断。
1.一个物体上、下两个面是相等的圆面,那么,它一定是圆柱形物体。 ( )
2.圆柱只有从上底面圆心到下底面圆心一条高。( )
3.圆柱体的表面积=底面积×2+底面积×高。( )
4.把两张相同的长方形纸,分别卷成两个形状不同的圆柱筒,并装上两个底那么制作的圆柱的高、侧面积、表面积一定相等。 ( )
5.侧面积相等的两个圆柱体,表面积也相等。( )
三、求下面圆柱的侧面积。
(1)底面周长为2.5 dm,高1.2 dm。
(2)底面直径为6 cm,高15 cm。
四、计算下面各圆柱的表面积。(单位:cm)
五、应用题
用铁皮做一个圆柱形通风管。通风管长3 m,横截面直径是2 dm。做这个通风管需要用多少平方分米铁皮?
六、应用题
给大厅中一根圆柱形立柱刷漆。已知立柱高4米,底面半径是0.5米,每平方米需油漆0.4千克。将这根立柱全部刷完共需多少千克油漆?
七、应用题
一个圆柱的高是31.4 dm,它的侧面展开后得到一个正方形。这个圆柱的表面积是多少?
八、应用题
如图,一个圆柱体被截去5 cm后,圆柱的表面积减少了31.4 cm2。求原来圆柱体的表面积是多少平方厘米?
(单位:cm)
九、应用题
下面是一张长方形纸板,按图示剪下阴影部分刚好能做成一个圆柱体。求做成的圆柱体的表面积。
十、应用题
如下图,高都是10厘米,底面半径分别是3厘米、6厘米的两个圆柱组成了一个几何体。求这个物体的表面积。
答案
一、(1)A (2)B (3)A (4)A
二、1.× 2.× 3.× 4.× 5.×
三、(1)2.5×1.2=3(dm2)
(2)3.14×6×15=282.6(cm2)
四、(1)侧面面积:3.14×5×20=314(cm2)
底面面积:2×3.14×(5÷2)2=39.25(cm2)
表面积:314+39.25=353.25(cm2)
(2)侧面面积:3.14×10×15=471(cm2)
底面面积:2×3.14×(10÷2)2=157(cm2)
表面积:471+157=628(cm2)
五、3m=30dm
3.14×2×30=188.4(平方分米)
六、2×3.14×0.5×4×0.4=5.024(千克)
七、31.4×31.4+3.14×(31.4÷3.14÷2)2×2=1142.96(dm2)
(分析:此圆柱的侧面展开的长方形的宽为圆柱的高即:31.4 dm,又因为是正方形,所以长也是31.4 dm,侧面展开面积可求,同时底面的周长也可知是31.4 dm,从而本可解。)
八、3.14×(31.4÷5÷3.14÷2)2×2+31.4÷5×20=131.88(平方厘米)
(分析:此题关键在于明白少的31.4 平方厘米是截去部分圆柱的侧面面积,与上底面面积无关。)
九、圆柱的底面直径:41.12÷(3.14+1+1)=8(cm)
圆柱的底面周长:41.12-8×2=25.12(cm)
圆柱的表面积:25.12×8+3.14×()2×2=301.44(cm2)
(分析:侧面展开图的长方形的长等于3.14个直径,而两个底面分别为一个直径,所以,本题中41.12 cm为(3.14+1+1)个直径,从而本题可解.)
十、物体表面积=大圆柱的表面积+小圆柱的侧面积=3.14×6×2×10+3.14×62×2+3.14×3×2×10=791.28(平方厘米)
(分析:本题关键在于两个圆柱的接合面面积不能加到表面积中,简易做法是:将小圆柱的上底面下移到大圆柱上,从面变为大圆柱的表面积与小圆柱侧面面积的和。)
