3.1.2导数的概念

项目 内容
课题 导数的概念（共 1 课时） 修改与创新
教学 目标 1．了解瞬时速度、瞬时变化率的概念； 2．理解导数的概念，知道瞬时变化率就是导数，体会导数的思想及其内涵；3．会求函数在某点的导数
教学重、难点 教学重点：瞬时速度、瞬时变化率的概念、导数的概念； 教学难点：导数的概念．
教学 准备 多媒体课件
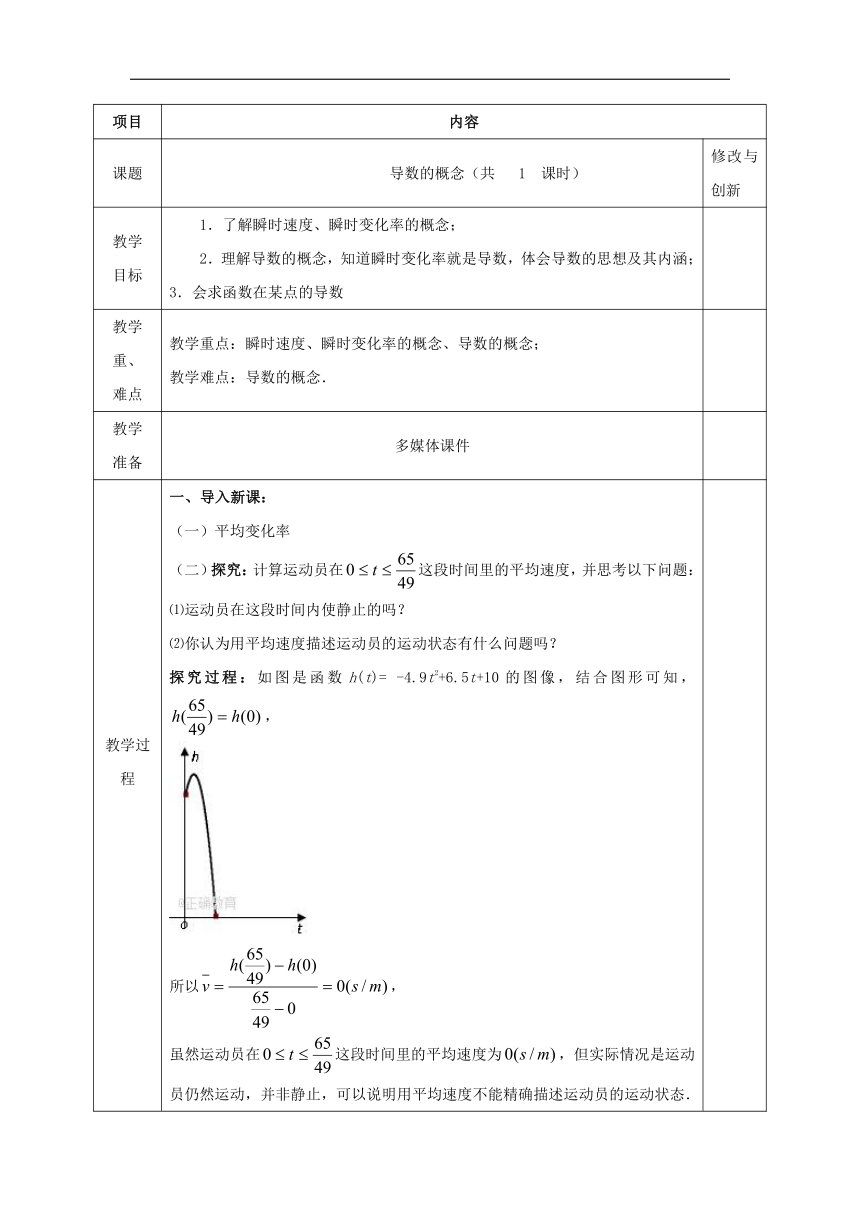
教学过程 一、导入新课：（一）平均变化率 （二）探究：计算运动员在这段时间里的平均速度，并思考以下问题：⑴运动员在这段时间内使静止的吗？ ⑵你认为用平均速度描述运动员的运动状态有什么问题吗？探究过程：如图是函数h(t)= -4.9t2+6.5t+10的图像，结合图形可知，， 所以， 虽然运动员在这段时间里的平均速度为，但实际情况是运动员仍然运动，并非静止，可以说明用平均速度不能精确描述运动员的运动状态．二、讲授新课：1．瞬时速度我们把物体在某一时刻的速度称为瞬时速度。运动员的平均速度不能反映他在某一时刻的瞬时速度，那么，如何求运动员的瞬时速度呢？比如，时的瞬时速度是多少？考察附近的情况： 思考：当趋近于0时，平均速度有什么样的变化趋势？ 结论：当趋近于0时，即无论从小于2的一边，还是从大于2的一边趋近于2时，平均速度都趋近于一个确定的值． 从物理的角度看，时间间隔无限变小时，平均速度就无限趋近于史的瞬时速度，因此，运动员在时的瞬时速度是 为了表述方便，我们用 表示“当，趋近于0时，平均速度趋近于定值”小结：局部以匀速代替变速，以平均速度代替瞬时速度，然后通过取极限，从瞬时速度的近似值过渡到瞬时速度的精确值。2 导数的概念从函数y=f(x)在x=x0处的瞬时变化率是:我们称它为函数在出的导数，记作或，即 说明：（1）导数即为函数y=f(x)在x=x0处的瞬时变化率 （2），当时，，所以三．典例分析 例1．（1）求函数y=3x2在x=1处的导数.分析：先求Δf=Δy=f(１＋Δx)-f(１)=6Δx+(Δx)2　　再求再求解：法一 定义法（略） 法二：（2）求函数f(x)=在附近的平均变化率，并求出在该点处的导数． 解： 例2．（课本例1）将原油精炼为汽油、柴油、塑胶等各种不同产品，需要对原油进行冷却和加热，如果第时，原油的温度（单位：）为，计算第时和第时，原油温度的瞬时变化率，并说明它们的意义． 解：在第时和第时，原油温度的瞬时变化率就是和 根据导数定义， 所以 同理可得:在第时和第时，原油温度的瞬时变化率分别为和5，说明在附近，原油温度大约以的速率下降，在第附近，原油温度大约以的速率上升． 注：一般地，反映了原油温度在时刻附近的变化情况．四．课堂练习1．质点运动规律为，求质点在的瞬时速度为． 2．求曲线y=f(x)=x3在时的导数．3．例2中，计算第时和第时，原油温度的瞬时变化率，并说明它们的意义． 课堂小结：1．瞬时速度、瞬时变化率的概念2．导数的概念 布置作业： P.80 A组,3,4
板书设计 §3.1.2导数的概念1．瞬时速度2 导数的概念例1．（1）求函数y=3x2在x=1处的导数.例2．（课本例1）练习1．质点运动规律为，求质点在的瞬时速度为． 2．求曲线y=f(x)=x3在时的导数．3．例2中，计算第时和第时，原油温度的瞬时变化率，并说明它们的意义．
教学反思 用平均速度和瞬时速度、平均膨胀率和瞬时膨胀率的关系，说明瞬时变化率的概念，以帮助学生理解瞬时变化率的意义，并由此给出导数的概念。 练习让学生自己独立完成，教师必要时给与指导。