人教版五上第7单元第1课时《不封闭路线的植树问题》(含答案及解析)
文档属性
| 名称 | 人教版五上第7单元第1课时《不封闭路线的植树问题》(含答案及解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 28.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-24 00:00:00 | ||
图片预览


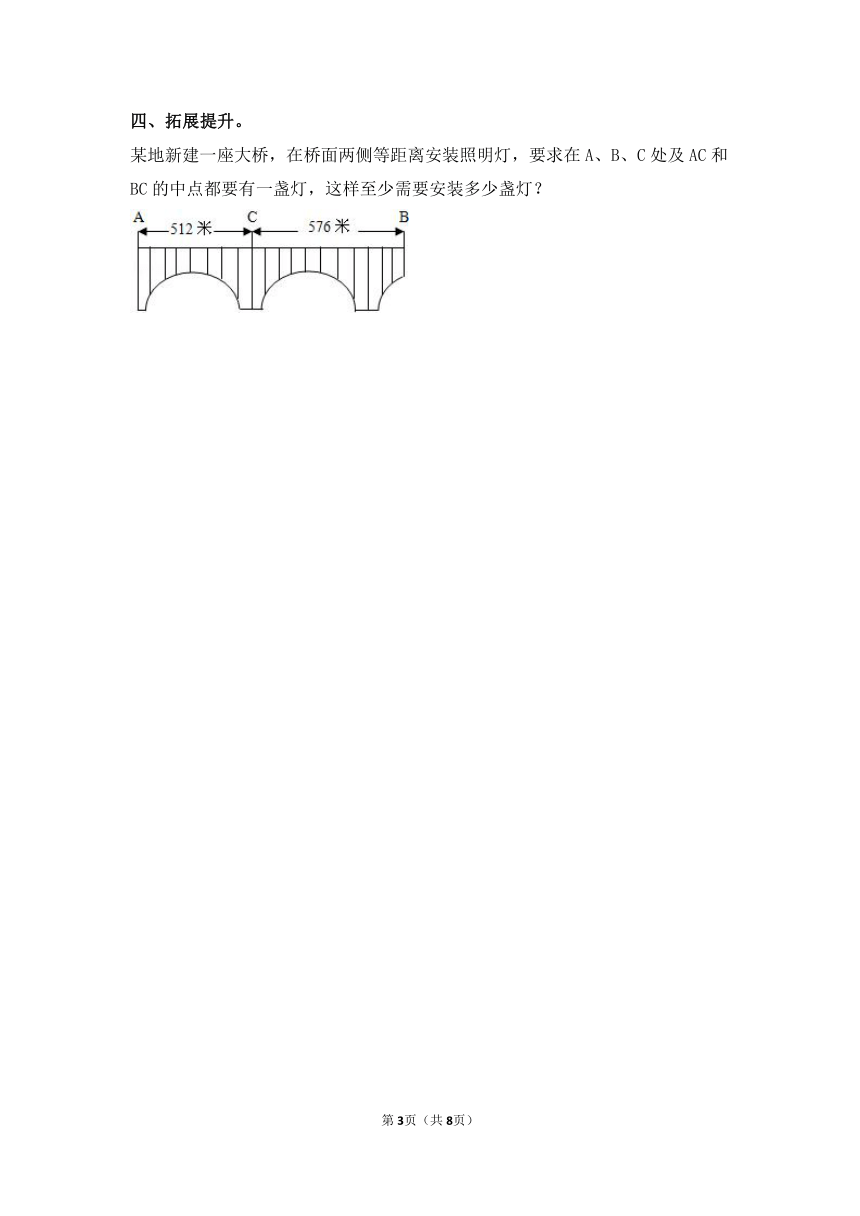

文档简介
第7单元第1课时《不封闭路线的植树问题》同步练习
一、单选题。
1、晶晶从一楼上到三楼走了36个台阶.她家住五楼,她到家一共要走( )级台阶.
A.48 B.60 C.72
2、为美化校园,学校在走道两旁每隔5米栽一棵风景树,学校走道大约2千米,那么一共栽( ).
A.800棵 B.402棵 C.802棵
3、一根木料,锯成三段需要6分钟.如果锯成10段需要( )分钟.
A.27 B.30 C.20
4、一条30米长的直道两边,每隔3米插一面彩旗.如果每边的两端都要插,一共需要( )面彩旗.
A.22 B.20 C.11
5、一只大钟敲三下要用3秒,这只大钟敲七下要用( )秒.
A.7 B.9 C.10 D.14
6、在100米的路段上植树,要保证至少有两棵树之间的距离小于10米,至少要种( )棵树.
A.9 B.10 C.11 D.12
7、在路边安装电线杆,每两根电线杆之间相距10米,从第一根到最后一根电线杆一共长100米,一共安装了多少?( )
A.9根 B.10根 C.11根
8、一条30米长的直道一边,每隔2米放了一盆花,一共要放16盆花.正确的放法是( ).
A.两端都放 B.只放一端 C.两端都不放
二、填空题。
1、每两根电杆间的距离是50米,小强从第一根电杆跑到第9根电杆,
共跑了 米.
2、在长90米的跑道一侧插10面彩旗(两端都插),每相邻两面彩旗之间
相距 米.
3、马路一边有一些电线杆,每两根电线杆中间有一个广告牌,已知广告牌有20个,那么电线杆 根.
4、同学们在全长100米的小路一边植树,每隔5米栽一棵(两端都栽).一共需要 棵树苗.
5、一座大楼共28层,每两层间楼梯阶数都相同.已知甲上楼的速度比乙快一倍,当甲到达第13层时,乙在第 层.
三、解答题。
1、社区要在300米的道路两侧安装路灯,每隔10米安装一盏(两端都安),一共需要多少盏路灯?
2、学校要在操场旁种一排树,每隔8米种1棵.
(1)从第1棵到第15棵相隔多少米?
(2)一共种了29棵树,这个操场有多长?
3、亮亮参加冬季长跑比赛,从出发开始每隔500米设一个服务站(出发点也有一个),当多多看到第5个服务站时,他跑了多少米?
4、园林工人沿公路一侧植树,每隔6米种一棵,一共种了36棵.从第1棵到最后一棵的距离有多远?
四、拓展提升。
某地新建一座大桥,在桥面两侧等距离安装照明灯,要求在A、B、C处及AC和BC的中点都要有一盏灯,这样至少需要安装多少盏灯?
参考答案
一、单选题。
1、
【答案】C
【解析】根据“从一楼到三楼走了36个台阶,”知道走了(3﹣1)个间隔是36个台阶,由此求出走1个间隔的台阶数;要求“住五楼一共要走的台阶数”,即求(5﹣1)个间隔数的台阶数,由此用间隔数乘1个间隔数的台阶数即可.
36÷(3﹣1)×(5﹣1)
=36÷2×4
=18×4
=72(级)
2、
【答案】 C
【解析】用2千米除以5米求出2千米里面有几个5米,即有几个间隔数,再加1就是学校在一旁植树的棵数,最后乘2就是一共植树的棵数.
2千米=2000米,
=(2000÷5+1)×2
=(400+1)×2
=401×2
=802(棵)
3、
【答案】A
【解析】锯3段,需要锯2次,由此先求出锯1次需要的时间是6÷2=3分钟,若锯成10段,则需要锯9次,由此利用乘法的意义即可答案.
6÷(3﹣1)×(10﹣1)
=6÷2×9
=27(分钟)
4、
【答案】A
【解析】根据植树问题中的两端都要栽:棵数=间隔数+1,来列式解答.
(30÷3+1)×2,
=11×2,
=22(面)
5、
【答案】B
【解析】敲响3下,经历了3﹣1=2个时间间隔,由此可以求出1个时间间隔是3÷2=1.5秒,那么敲响7下,经历了7﹣1=6个时间间隔,再乘以6即可.
3÷(3﹣1)×(7﹣1)
=3÷2×6
=9(秒)
6、
【答案】D
【解析】两端都要栽时,间隔数=植树棵数﹣1,假设相邻两棵树之间的距离是10米,则需要植树100÷10+1=11,因为要保证至少有两棵树之间的距离小于10米,所以至少需要种11+1=12棵树.
100÷10+1+1
=10+1+1
=12(棵)
7、
【答案】C
【解析】每两根电线杆之间相距10米,从第一根到最后一根电线杆共长100米,也就是把100米平均分成10米长的若干小段,电线杆安在各分点上,因为两端都要安装电线杆,电线杆的数量等于段数加1.
100÷10+1
=10+1
=11(根)
8、
【答案】 A
【解析】盆的间隔数是:30÷2=15(个),因为16﹣15=1(盆),所以两端都放;据此答案.
二、填空题。
1、
【答案】400
【解析】由“从第一根电杆跑到第9根电杆,”得出小强是跑了9﹣1个间隔,由此用间隔数乘每两个间隔的距离求出小强跑的米数.
50×(9﹣1),
=50×8,
=400(米)
2、
【答案】10
【解析】因为长90米的跑道一侧插上10面彩旗(两端都插),说明是一个开放性的图形植树的问题,由此知道间隔数=彩旗的面数﹣1,所以用90除以间隔数就是每相邻两面彩旗之间相距的米数.
90÷(10﹣1),
=90÷9,
=10(米)
3、
【答案】 21
【解析】已知广告牌有20个,相当于20个间隔,那么电线杆有20+1=21(根);据此答案.
4、
【答案】21
【解析】植树问题中,两端都要栽时,植树棵数=间隔数+1,由此先用100÷5求得间隔数,再加上1即可.
100÷5+1
=20+1
=21(棵)
5、
【答案】 7
【解析】甲从1层上到13层,走的楼梯间隔数是:13﹣1=12个,那么乙走12÷2=6个,乙到达6+1=7(层);据此答案.
三、解答题。
1、
【解析】先求出300米里面有几个10,即有几个间隔,两端都安,由此得出一侧安装路灯的盏数,进而求出两侧安装路灯的盏数.
【答案】解:300÷10+1
=30+1
=31(盏)
31×2=62(盏)
答:一共需要62盏路灯.
2、
【解析】(1)从第1棵树到第15棵树,间隔数是15﹣1=14个,然后用间距乘间隔数即可;
(2)一共种了29棵树,间隔数是29﹣1=28个,然后用间距乘间隔数即可求出这个操场有多长.
【答案】解:(1)8×(15﹣1)
=8×14
=112(米)
答:从第1棵到第15棵相隔112米.
(2)8×(29﹣1)
=8×28
=224(米)
答:这个操场长224米.
3、
【解析】因为从起点开始设服务站,所以当亮亮跑到第5个服务站时,实际上跑了(5﹣1)个间隔的距离,由此根据整数乘法的意义,用间距500乘间隔数4答案即可.
【答案】解:500×(5﹣1)
=500×4
=2000(米)
答:他跑了2000米.
4、
【解析】根据题干,此题属于两端都要栽的情况:间隔数=植树棵数﹣1,由此可以求出从第1棵到最后一棵之间有36﹣1=35个间隔,再乘以6即可解决问题.
【答案】解:(36﹣1)×6
=35×6
=210(米)
答:从第1棵到最后一棵的距离是210米.
四、拓展提升。
【解析】要在A、B、C处及AC和BC的中点都要有一盏灯,这五个点到桥头的距离必须是灯距的倍数;AC的中间距是512÷2=256米;BC的中间距是576÷2=288米;要求至少需要安装多少盏灯,就必须使灯距最大,也就是求256和288的最大公约数,然后用(512+576)除以最大公约数再加1,即是每边的盏数,然后再乘2即可求出两边一共安装的盏数.
【答案】解:512÷2=256(米),
576÷2=288(米);
256=2×2×2×2×2×2×2×2,
288=2×2×2×2×2×3×3,
256和288的最大公约数是:2×2×2×2×2=32,
所以灯距最大是32米;
(512+576)÷32+1,
=34+1,
=35(盏);
35×2=70(盏);
答:至少需要安装70盏灯.
第1页(共8页)
一、单选题。
1、晶晶从一楼上到三楼走了36个台阶.她家住五楼,她到家一共要走( )级台阶.
A.48 B.60 C.72
2、为美化校园,学校在走道两旁每隔5米栽一棵风景树,学校走道大约2千米,那么一共栽( ).
A.800棵 B.402棵 C.802棵
3、一根木料,锯成三段需要6分钟.如果锯成10段需要( )分钟.
A.27 B.30 C.20
4、一条30米长的直道两边,每隔3米插一面彩旗.如果每边的两端都要插,一共需要( )面彩旗.
A.22 B.20 C.11
5、一只大钟敲三下要用3秒,这只大钟敲七下要用( )秒.
A.7 B.9 C.10 D.14
6、在100米的路段上植树,要保证至少有两棵树之间的距离小于10米,至少要种( )棵树.
A.9 B.10 C.11 D.12
7、在路边安装电线杆,每两根电线杆之间相距10米,从第一根到最后一根电线杆一共长100米,一共安装了多少?( )
A.9根 B.10根 C.11根
8、一条30米长的直道一边,每隔2米放了一盆花,一共要放16盆花.正确的放法是( ).
A.两端都放 B.只放一端 C.两端都不放
二、填空题。
1、每两根电杆间的距离是50米,小强从第一根电杆跑到第9根电杆,
共跑了 米.
2、在长90米的跑道一侧插10面彩旗(两端都插),每相邻两面彩旗之间
相距 米.
3、马路一边有一些电线杆,每两根电线杆中间有一个广告牌,已知广告牌有20个,那么电线杆 根.
4、同学们在全长100米的小路一边植树,每隔5米栽一棵(两端都栽).一共需要 棵树苗.
5、一座大楼共28层,每两层间楼梯阶数都相同.已知甲上楼的速度比乙快一倍,当甲到达第13层时,乙在第 层.
三、解答题。
1、社区要在300米的道路两侧安装路灯,每隔10米安装一盏(两端都安),一共需要多少盏路灯?
2、学校要在操场旁种一排树,每隔8米种1棵.
(1)从第1棵到第15棵相隔多少米?
(2)一共种了29棵树,这个操场有多长?
3、亮亮参加冬季长跑比赛,从出发开始每隔500米设一个服务站(出发点也有一个),当多多看到第5个服务站时,他跑了多少米?
4、园林工人沿公路一侧植树,每隔6米种一棵,一共种了36棵.从第1棵到最后一棵的距离有多远?
四、拓展提升。
某地新建一座大桥,在桥面两侧等距离安装照明灯,要求在A、B、C处及AC和BC的中点都要有一盏灯,这样至少需要安装多少盏灯?
参考答案
一、单选题。
1、
【答案】C
【解析】根据“从一楼到三楼走了36个台阶,”知道走了(3﹣1)个间隔是36个台阶,由此求出走1个间隔的台阶数;要求“住五楼一共要走的台阶数”,即求(5﹣1)个间隔数的台阶数,由此用间隔数乘1个间隔数的台阶数即可.
36÷(3﹣1)×(5﹣1)
=36÷2×4
=18×4
=72(级)
2、
【答案】 C
【解析】用2千米除以5米求出2千米里面有几个5米,即有几个间隔数,再加1就是学校在一旁植树的棵数,最后乘2就是一共植树的棵数.
2千米=2000米,
=(2000÷5+1)×2
=(400+1)×2
=401×2
=802(棵)
3、
【答案】A
【解析】锯3段,需要锯2次,由此先求出锯1次需要的时间是6÷2=3分钟,若锯成10段,则需要锯9次,由此利用乘法的意义即可答案.
6÷(3﹣1)×(10﹣1)
=6÷2×9
=27(分钟)
4、
【答案】A
【解析】根据植树问题中的两端都要栽:棵数=间隔数+1,来列式解答.
(30÷3+1)×2,
=11×2,
=22(面)
5、
【答案】B
【解析】敲响3下,经历了3﹣1=2个时间间隔,由此可以求出1个时间间隔是3÷2=1.5秒,那么敲响7下,经历了7﹣1=6个时间间隔,再乘以6即可.
3÷(3﹣1)×(7﹣1)
=3÷2×6
=9(秒)
6、
【答案】D
【解析】两端都要栽时,间隔数=植树棵数﹣1,假设相邻两棵树之间的距离是10米,则需要植树100÷10+1=11,因为要保证至少有两棵树之间的距离小于10米,所以至少需要种11+1=12棵树.
100÷10+1+1
=10+1+1
=12(棵)
7、
【答案】C
【解析】每两根电线杆之间相距10米,从第一根到最后一根电线杆共长100米,也就是把100米平均分成10米长的若干小段,电线杆安在各分点上,因为两端都要安装电线杆,电线杆的数量等于段数加1.
100÷10+1
=10+1
=11(根)
8、
【答案】 A
【解析】盆的间隔数是:30÷2=15(个),因为16﹣15=1(盆),所以两端都放;据此答案.
二、填空题。
1、
【答案】400
【解析】由“从第一根电杆跑到第9根电杆,”得出小强是跑了9﹣1个间隔,由此用间隔数乘每两个间隔的距离求出小强跑的米数.
50×(9﹣1),
=50×8,
=400(米)
2、
【答案】10
【解析】因为长90米的跑道一侧插上10面彩旗(两端都插),说明是一个开放性的图形植树的问题,由此知道间隔数=彩旗的面数﹣1,所以用90除以间隔数就是每相邻两面彩旗之间相距的米数.
90÷(10﹣1),
=90÷9,
=10(米)
3、
【答案】 21
【解析】已知广告牌有20个,相当于20个间隔,那么电线杆有20+1=21(根);据此答案.
4、
【答案】21
【解析】植树问题中,两端都要栽时,植树棵数=间隔数+1,由此先用100÷5求得间隔数,再加上1即可.
100÷5+1
=20+1
=21(棵)
5、
【答案】 7
【解析】甲从1层上到13层,走的楼梯间隔数是:13﹣1=12个,那么乙走12÷2=6个,乙到达6+1=7(层);据此答案.
三、解答题。
1、
【解析】先求出300米里面有几个10,即有几个间隔,两端都安,由此得出一侧安装路灯的盏数,进而求出两侧安装路灯的盏数.
【答案】解:300÷10+1
=30+1
=31(盏)
31×2=62(盏)
答:一共需要62盏路灯.
2、
【解析】(1)从第1棵树到第15棵树,间隔数是15﹣1=14个,然后用间距乘间隔数即可;
(2)一共种了29棵树,间隔数是29﹣1=28个,然后用间距乘间隔数即可求出这个操场有多长.
【答案】解:(1)8×(15﹣1)
=8×14
=112(米)
答:从第1棵到第15棵相隔112米.
(2)8×(29﹣1)
=8×28
=224(米)
答:这个操场长224米.
3、
【解析】因为从起点开始设服务站,所以当亮亮跑到第5个服务站时,实际上跑了(5﹣1)个间隔的距离,由此根据整数乘法的意义,用间距500乘间隔数4答案即可.
【答案】解:500×(5﹣1)
=500×4
=2000(米)
答:他跑了2000米.
4、
【解析】根据题干,此题属于两端都要栽的情况:间隔数=植树棵数﹣1,由此可以求出从第1棵到最后一棵之间有36﹣1=35个间隔,再乘以6即可解决问题.
【答案】解:(36﹣1)×6
=35×6
=210(米)
答:从第1棵到最后一棵的距离是210米.
四、拓展提升。
【解析】要在A、B、C处及AC和BC的中点都要有一盏灯,这五个点到桥头的距离必须是灯距的倍数;AC的中间距是512÷2=256米;BC的中间距是576÷2=288米;要求至少需要安装多少盏灯,就必须使灯距最大,也就是求256和288的最大公约数,然后用(512+576)除以最大公约数再加1,即是每边的盏数,然后再乘2即可求出两边一共安装的盏数.
【答案】解:512÷2=256(米),
576÷2=288(米);
256=2×2×2×2×2×2×2×2,
288=2×2×2×2×2×3×3,
256和288的最大公约数是:2×2×2×2×2=32,
所以灯距最大是32米;
(512+576)÷32+1,
=34+1,
=35(盏);
35×2=70(盏);
答:至少需要安装70盏灯.
第1页(共8页)
