人教版九年级数学 上册22.1.4用函数观点看一元二次方程 教案(表格式)
文档属性
| 名称 | 人教版九年级数学 上册22.1.4用函数观点看一元二次方程 教案(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 41.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-22 00:00:00 | ||
图片预览


文档简介
九年级上数学
集体备课教学案 (25)
主备人: 备课组长:
课 题 22.1.4 用函数观点看一元二次方程 课 时 1
执教者 课 型 单一
时 间 教 具 投影仪
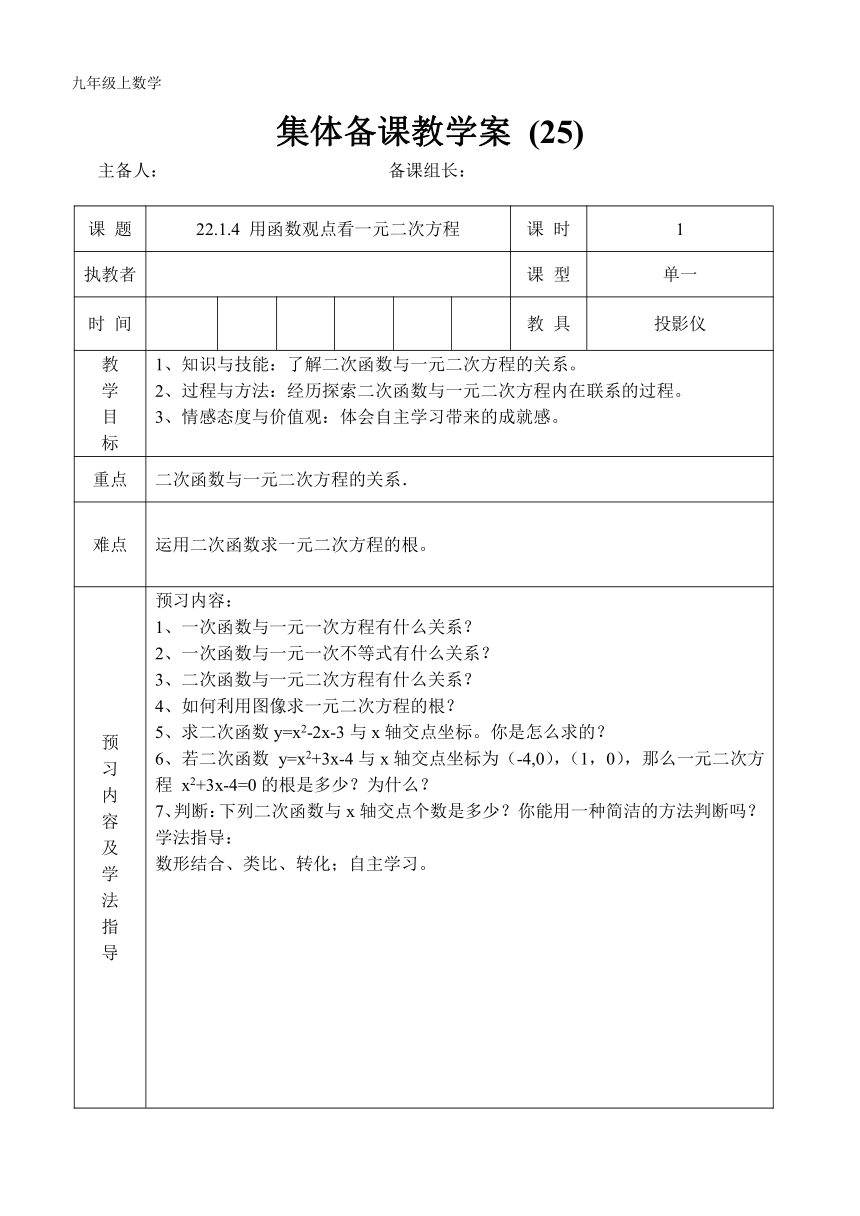
教 学 目 标 1、知识与技能:了解二次函数与一元二次方程的关系。2、过程与方法:经历探索二次函数与一元二次方程内在联系的过程。 3、情感态度与价值观:体会自主学习带来的成就感。
重点 二次函数与一元二次方程的关系.
难点 运用二次函数求一元二次方程的根。
预 习 内 容 及 学 法 指 导 预习内容: 1、一次函数与一元一次方程有什么关系? 2、一次函数与一元一次不等式有什么关系? 3、二次函数与一元二次方程有什么关系? 4、如何利用图像求一元二次方程的根? 5、求二次函数y=x2-2x-3与x轴交点坐标。你是怎么求的? 6、若二次函数 y=x2+3x-4与x轴交点坐标为(-4,0),(1,0),那么一元二次方程 x2+3x-4=0的根是多少?为什么? 7、判断:下列二次函数与x轴交点个数是多少?你能用一种简洁的方法判断吗? 学法指导: 数形结合、类比、转化;自主学习。
学 习 过 程
教学流程及时间 教师行为(活动) 学生行为(活动) 二次备课
创设情境 揭示课题 2分钟 出示目标 交流预习 5分钟 引导探究 小组展示 15分钟 一次函数与一元一次方程有密切的关系。二次函数与一元二次方程也有着密切的关系。 感受二次函数与一元二次方程内在联系。 利用二次函数的图像求一元二次方程的根。 1、小组内先检查、补充预习作业。交流方法,解决疑惑。 2、小组代表展示展示预习作业。采用树形结合的方法。类比一次函数与一元一次方程的关系。 3、归纳出二次函数与一元二次方程的关系。 4、学生借助一元二次方程根的判别式,来判断二次函数与x轴交点个数。 感受。对比。联系。类比。 学生体会本节课的努力方向。 学生互相交流。 学生评价,纠错,补充,质疑。小组加分。 学生类比描述二次函数与一元二次方程的关系。 学生体会一元二次方程根情况与二次函数与 x轴交点个数之间的关系。
教学流程及时间 教师行为(活动) 学生行为(活动) 二次备课
精讲点拨 质疑释疑 13分钟 以举例的形式,让学生深入体会二次函数与一元二次方程的关系。 如:若二次函数y=ax2+bx+c与x轴交点坐标是(2,0),(5,0),则一元二次方程ax2+bx+c=0的解是多少? 引导学生以表格的形式,整理:如何利用根的判别式判断二次函数与x轴交点个数,同时对比用根的判别式判断一元二次方程解的情况。 3、列举几个有关的题目,由学生自主解答。有疑问之处,可以相互研究。 学生类比一元一次方程与一次函数的关系,自主解决这个题目。 认真聆听教师的讲解。 学生自主整理,有疑问的地方聆听老师的解释。 运用知识的归纳解决相关问题。认真聆听老师的分析,同学的讲解。
小 结 提 升 2分钟 二次函数与一元二次方程有什么关系?你用什么方法帮助你理解记忆? 如何判断二次函数与x轴交点个数?你用什么方法帮助你理解记忆? 评价你及你的小组或其他小组的表现? 本节课用到的数学方法有什么?
达 标 检 测 8分钟 二次函数y=2x2-2x-3与x轴交点坐标为-------------。 二次函数y=-3x2+4x-3与x轴交点个数为------------。 二次函数y=-x2-2x+3与x轴交点坐标为---------,与 y轴交点坐标为---------。若二次函数 y=ax2+bx+c的图像始终在x轴的上方,则-----------。若二次函数 y=ax2+bx+c的图像始终在x轴的下方,则-----------。
布置 作业 同步练习册
板 书 设 计 22.1.4 用函数观点看一元二次方程 二次函数与一元二次方程的关系 典型例题 二次函数与x轴交点个数的确定 练习展示
教学 反思
同课章节目录
