高中数学人教A版必修三课件 1.1.2 第2课时 条件结构 :23张PPT
文档属性
| 名称 | 高中数学人教A版必修三课件 1.1.2 第2课时 条件结构 :23张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1003.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览





文档简介
课件23张PPT。第2课时 条件结构一、条件结构的概念
1.解关于x的方程ax+b=0的算法步骤如何设计?
提示第一步,输入实数a,b.
第二步,判断a是否为0.若是,执行第三步;否则,计算x=- ,并输出x,结束算法.
第三步,判断b是否为0.若是,则输出“方程的解为任意实数”;否则,输出“方程无实数解”.2.问题1中的算法的程序框图还能不能只用顺序结构表示?为什么?
提示不能.从算法中的第二步对a进行分类讨论可以看出,当a为0与否时方程有不同的解,所以程序框图不能由若干个依次执行的步骤组成,因此不能只用顺序结构表示.
3.什么是条件结构?
提示在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.4.做一做1:判断题
(1)条件结构的出口有两个,但在执行时,只有一个出口是有效的. ( )
(2)条件结构的判断条件要写在判断框内. ( )
答案:(1)√ (2)√二、条件结构程序框图的形式
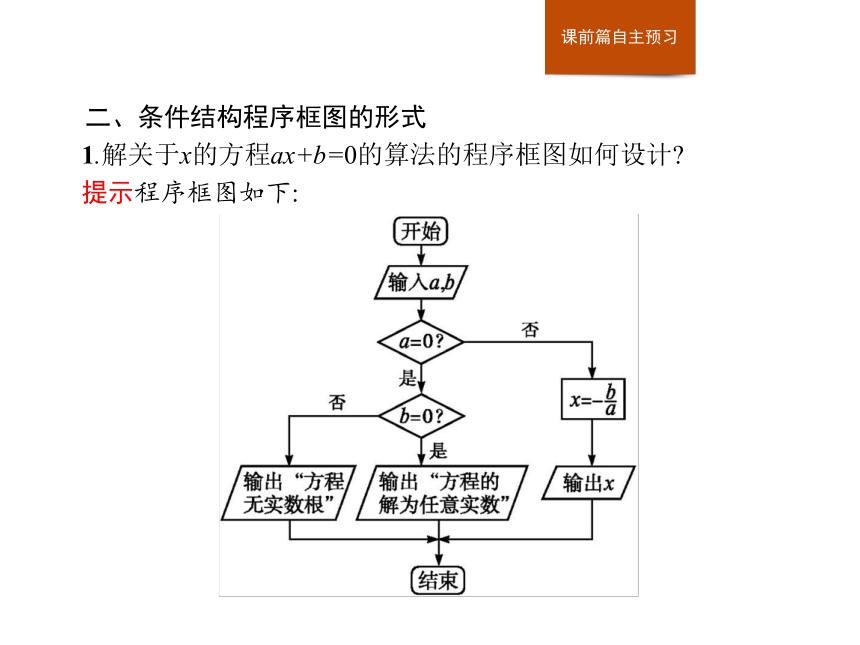
1.解关于x的方程ax+b=0的算法的程序框图如何设计?
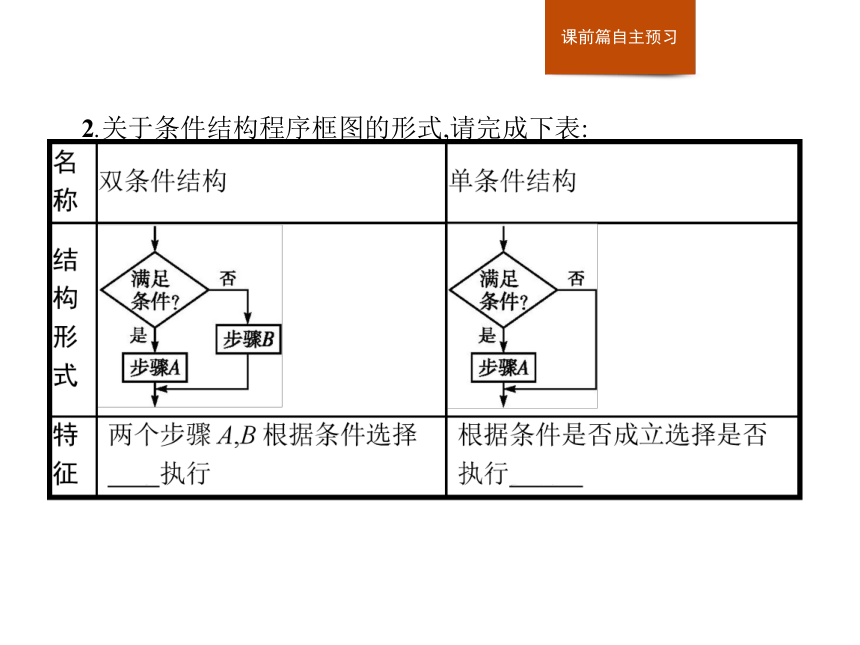
提示程序框图如下:2.关于条件结构程序框图的形式,请完成下表: 3.做一做2:判断题
(1)条件结构根据条件是否成立,选择不同的分支执行. ( )
(2)条件结构与顺序结构的明显区别在于条件结构中含有判断框,而顺序结构中不含判断框. ( )
答案:(1)√ (2)√4.做一做3:下列问题的算法适宜用条件结构表示的是( )
A.求点P(-1,3)到直线l:3x-2y+1=0的距离
B.由直角三角形的两条直角边求斜边
C.解不等式ax+b>0(a≠0)
D.计算100个数的平均数
解析:条件结构是处理逻辑判断并根据判断进行不同处理的结构,只有选项C中需要判断a的正、负,其余选项中都不含逻辑判断.
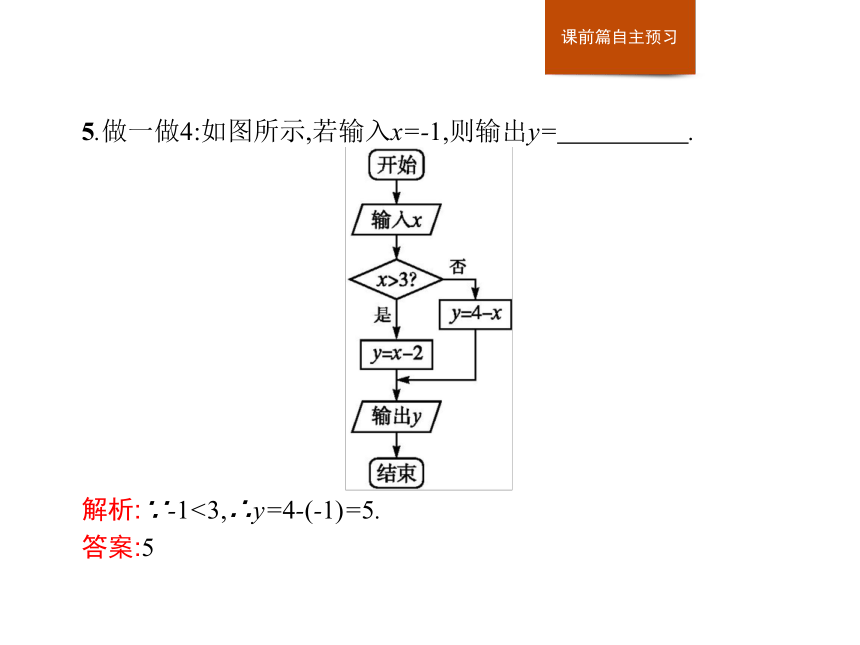
答案:C5.做一做4:如图所示,若输入x=-1,则输出y= .
?
解析:∵-1<3,∴y=4-(-1)=5.
答案:5探究一探究二探究三简单条件结构程序框图的设计
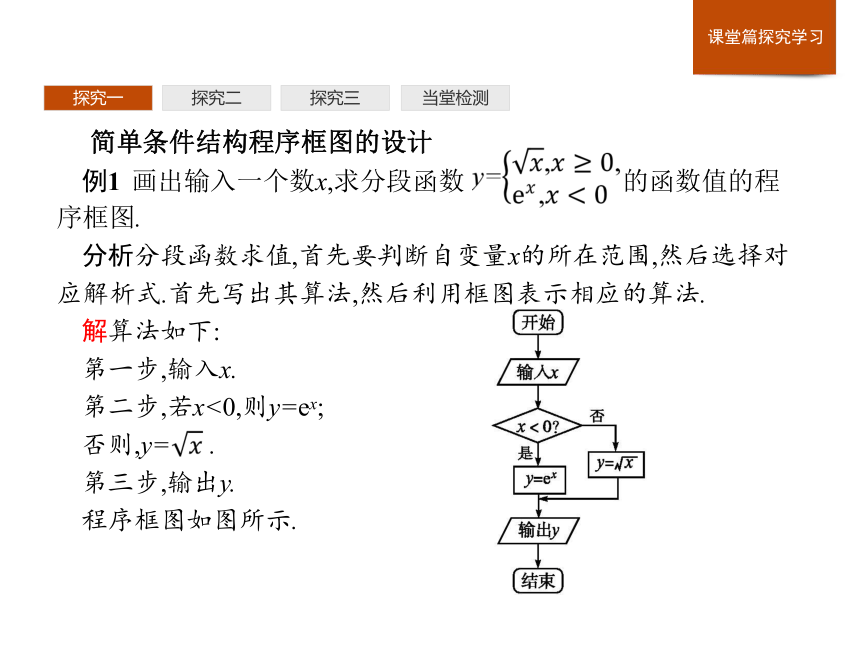
例1 画出输入一个数x,求分段函数 的函数值的程序框图.
分析分段函数求值,首先要判断自变量x的所在范围,然后选择对应解析式.首先写出其算法,然后利用框图表示相应的算法.
解算法如下:
第一步,输入x.
第二步,若x<0,则y=ex;
否则,y= .
第三步,输出y.
程序框图如图所示.当堂检测探究一探究二探究三反思感悟1.本题因x的符号不定,从而引起y值对应关系的变化.
2.解决分类讨论问题时,一般需要用条件结构来设计算法,解决此类问题的关键是首先设计好判断框内的条件,然后根据条件是否成立选择不同的流向.
3.利用条件结构解决数学问题需注意分析题目,确定分类标准和方法,明确每个分类中执行的步骤.当堂检测探究一探究二探究三互动探究1如果【例1】中判断框图内的条件改为x≥0,所画程序框图应该如何改动?
分析根据分段函数解析式与自变量取值范围的对应,只需把“是”“否”对换即可;或者直接把两个处理框互换.
解程序框图如图所示.当堂检测探究一探究二探究三 分析该函数为分段函数,当给出一个自变量x的值时,需首先判断x的取值范围,然后确定解析式求函数值,故在画程序框图时要用到两个判断框.条件结构的嵌套 当堂检测探究一探究二探究三解:算法如下:
第一步,输入x.
第二步,若x<0,则y=2x-1,输出y,结束算法;
否则,执行第三步.
第三步,若x<1,则y=x2+1,输出y,结束算法;
否则,执行第四步.
第四步,y=x3+2x,输出y,结束算法.
程序框图如图所示.当堂检测探究一探究二探究三反思感悟1.在程序设计中,程序的流向要多次根据判断做出选择时,一般要用到条件结构的嵌套.
2.条件结构的嵌套是指在一个条件结构的分支内的步骤中又用到条件结构,就像一个条件结构镶嵌在另一个条件结构中一样.
3.在用到条件结构的嵌套时,一定要分清主次,弄清每个判断框中的条件,以及满足条件时程序的流向.当堂检测探究一探究二探究三互动探究2在【例2】的解析中如果先判断x≥1,程序框图应怎么改?
分析先判断x≥1,则第二步就判断x<0是否成立,只需调整相应的处理框.
解算法如下:
第一步,输入x.
第二步,如果x≥1,那么y=x3+2x,执行
第五步;否则,执行第三步.
第三步,如果x<0,那么使y=2x-1,执行
第五步;否则,执行第四步.
第四步,y=x2+1.
第五步,输出y.
程序框图如图所示.当堂检测探究一探究二探究三例3 某商场购物实行优惠措施,若购物金额在800元以上(包括800元),则打八折;若购物金额在500元以上(包括500元),但不到800元,则打九折;否则不打折,设计算法并画出程序框图,要求输入购物金额,能输出实际交款额.条件结构在实际中的应用 当堂检测探究一探究二探究三解:设购物金额为x元时,实际交款y元,
算法如下:
第一步,输入x.
第二步,若x≥800,则y=0.8x,输出y,结束算法;否则,执行第三步.
第三步,若x≥500,则y=0.9x;否则,y=x.
第四步,输出y.
程序框图如图所示.当堂检测探究一探究二探究三反思感悟设计程序框图解决实际问题的步骤
(1)读懂题意,分析已知和未知的关系;
(2)概括题意写出表达式;
(3)设计算法步骤;
(4)根据算法步骤画出程序框图.当堂检测探究一探究二探究三变式训练某居民区的物业管理部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,画出程序框图.
解:算法过程如下:
第一步,输入x.
第二步,若x≤3,则y=5;否则,y=5+1.2(x-3).
第三步,输出y.
程序框图如图所示.当堂检测1.解决下列问题的算法中,需要条件结构的是( )
A.求两个数的和
B.求某个正实数的常用对数
C.求半径为r的圆的面积
D.解关于x的一元二次方程ax2+bx+c=0
解析:解关于x的一元二次方程ax2+bx+c=0时,需判断Δ=b2-4ac与0的大小关系,故需要条件结构.
答案:D探究一探究二探究三当堂检测2.下面程序框图的运算结果为( )
A.5 B.10 C.15 D.20
解析:运行程序:a=5≥4成立,则S=1×5=5,故选A.
答案:A探究一探究二探究三当堂检测3.某市的出租车收费办法如下:不超过2 km收7元(即起步价7元),超过2 km的里程每千米收2.6元,另每车次超过2 km收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
A.y=7+2.6x B.y=8+2.6x
C.y=7+2.6(x-2) D.y=8+2.6(x-2)探究一探究二探究三当堂检测解析:当x>2时,2 km内的收费为7元,2 km外的收费为(x-2)×2.6,另外燃油附加费为1元,
故y=7+2.6(x-2)+1=8+2.6(x-2).
答案:D探究一探究二探究三当堂检测
1.解关于x的方程ax+b=0的算法步骤如何设计?
提示第一步,输入实数a,b.
第二步,判断a是否为0.若是,执行第三步;否则,计算x=- ,并输出x,结束算法.
第三步,判断b是否为0.若是,则输出“方程的解为任意实数”;否则,输出“方程无实数解”.2.问题1中的算法的程序框图还能不能只用顺序结构表示?为什么?
提示不能.从算法中的第二步对a进行分类讨论可以看出,当a为0与否时方程有不同的解,所以程序框图不能由若干个依次执行的步骤组成,因此不能只用顺序结构表示.
3.什么是条件结构?
提示在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.4.做一做1:判断题
(1)条件结构的出口有两个,但在执行时,只有一个出口是有效的. ( )
(2)条件结构的判断条件要写在判断框内. ( )
答案:(1)√ (2)√二、条件结构程序框图的形式
1.解关于x的方程ax+b=0的算法的程序框图如何设计?
提示程序框图如下:2.关于条件结构程序框图的形式,请完成下表: 3.做一做2:判断题
(1)条件结构根据条件是否成立,选择不同的分支执行. ( )
(2)条件结构与顺序结构的明显区别在于条件结构中含有判断框,而顺序结构中不含判断框. ( )
答案:(1)√ (2)√4.做一做3:下列问题的算法适宜用条件结构表示的是( )
A.求点P(-1,3)到直线l:3x-2y+1=0的距离
B.由直角三角形的两条直角边求斜边
C.解不等式ax+b>0(a≠0)
D.计算100个数的平均数
解析:条件结构是处理逻辑判断并根据判断进行不同处理的结构,只有选项C中需要判断a的正、负,其余选项中都不含逻辑判断.
答案:C5.做一做4:如图所示,若输入x=-1,则输出y= .
?
解析:∵-1<3,∴y=4-(-1)=5.
答案:5探究一探究二探究三简单条件结构程序框图的设计
例1 画出输入一个数x,求分段函数 的函数值的程序框图.
分析分段函数求值,首先要判断自变量x的所在范围,然后选择对应解析式.首先写出其算法,然后利用框图表示相应的算法.
解算法如下:
第一步,输入x.
第二步,若x<0,则y=ex;
否则,y= .
第三步,输出y.
程序框图如图所示.当堂检测探究一探究二探究三反思感悟1.本题因x的符号不定,从而引起y值对应关系的变化.
2.解决分类讨论问题时,一般需要用条件结构来设计算法,解决此类问题的关键是首先设计好判断框内的条件,然后根据条件是否成立选择不同的流向.
3.利用条件结构解决数学问题需注意分析题目,确定分类标准和方法,明确每个分类中执行的步骤.当堂检测探究一探究二探究三互动探究1如果【例1】中判断框图内的条件改为x≥0,所画程序框图应该如何改动?
分析根据分段函数解析式与自变量取值范围的对应,只需把“是”“否”对换即可;或者直接把两个处理框互换.
解程序框图如图所示.当堂检测探究一探究二探究三 分析该函数为分段函数,当给出一个自变量x的值时,需首先判断x的取值范围,然后确定解析式求函数值,故在画程序框图时要用到两个判断框.条件结构的嵌套 当堂检测探究一探究二探究三解:算法如下:
第一步,输入x.
第二步,若x<0,则y=2x-1,输出y,结束算法;
否则,执行第三步.
第三步,若x<1,则y=x2+1,输出y,结束算法;
否则,执行第四步.
第四步,y=x3+2x,输出y,结束算法.
程序框图如图所示.当堂检测探究一探究二探究三反思感悟1.在程序设计中,程序的流向要多次根据判断做出选择时,一般要用到条件结构的嵌套.
2.条件结构的嵌套是指在一个条件结构的分支内的步骤中又用到条件结构,就像一个条件结构镶嵌在另一个条件结构中一样.
3.在用到条件结构的嵌套时,一定要分清主次,弄清每个判断框中的条件,以及满足条件时程序的流向.当堂检测探究一探究二探究三互动探究2在【例2】的解析中如果先判断x≥1,程序框图应怎么改?
分析先判断x≥1,则第二步就判断x<0是否成立,只需调整相应的处理框.
解算法如下:
第一步,输入x.
第二步,如果x≥1,那么y=x3+2x,执行
第五步;否则,执行第三步.
第三步,如果x<0,那么使y=2x-1,执行
第五步;否则,执行第四步.
第四步,y=x2+1.
第五步,输出y.
程序框图如图所示.当堂检测探究一探究二探究三例3 某商场购物实行优惠措施,若购物金额在800元以上(包括800元),则打八折;若购物金额在500元以上(包括500元),但不到800元,则打九折;否则不打折,设计算法并画出程序框图,要求输入购物金额,能输出实际交款额.条件结构在实际中的应用 当堂检测探究一探究二探究三解:设购物金额为x元时,实际交款y元,
算法如下:
第一步,输入x.
第二步,若x≥800,则y=0.8x,输出y,结束算法;否则,执行第三步.
第三步,若x≥500,则y=0.9x;否则,y=x.
第四步,输出y.
程序框图如图所示.当堂检测探究一探究二探究三反思感悟设计程序框图解决实际问题的步骤
(1)读懂题意,分析已知和未知的关系;
(2)概括题意写出表达式;
(3)设计算法步骤;
(4)根据算法步骤画出程序框图.当堂检测探究一探究二探究三变式训练某居民区的物业管理部门每月向居民收取卫生费,计费方法是:3人和3人以下的住户,每户收取5元;超过3人的住户,每超出1人加收1.2元.设计一个算法,根据输入的人数,计算应收取的卫生费,画出程序框图.
解:算法过程如下:
第一步,输入x.
第二步,若x≤3,则y=5;否则,y=5+1.2(x-3).
第三步,输出y.
程序框图如图所示.当堂检测1.解决下列问题的算法中,需要条件结构的是( )
A.求两个数的和
B.求某个正实数的常用对数
C.求半径为r的圆的面积
D.解关于x的一元二次方程ax2+bx+c=0
解析:解关于x的一元二次方程ax2+bx+c=0时,需判断Δ=b2-4ac与0的大小关系,故需要条件结构.
答案:D探究一探究二探究三当堂检测2.下面程序框图的运算结果为( )
A.5 B.10 C.15 D.20
解析:运行程序:a=5≥4成立,则S=1×5=5,故选A.
答案:A探究一探究二探究三当堂检测3.某市的出租车收费办法如下:不超过2 km收7元(即起步价7元),超过2 km的里程每千米收2.6元,另每车次超过2 km收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填( )
A.y=7+2.6x B.y=8+2.6x
C.y=7+2.6(x-2) D.y=8+2.6(x-2)探究一探究二探究三当堂检测解析:当x>2时,2 km内的收费为7元,2 km外的收费为(x-2)×2.6,另外燃油附加费为1元,
故y=7+2.6(x-2)+1=8+2.6(x-2).
答案:D探究一探究二探究三当堂检测
