高中数学人教A版必修三课件 1.1.2 第3课时 循环结构 :31张PPT
文档属性
| 名称 | 高中数学人教A版必修三课件 1.1.2 第3课时 循环结构 :31张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览








文档简介
课件31张PPT。第3课时 循环结构一、循环结构、循环体的概念
1.在申办奥运会的最后阶段,你知道国际奥委会是如何通过投票决定主办权归属的吗?对竞选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票数超过总票数的一半,那么该城市就获得主办权;如果所有申办城市得票数都不超过总票数的一半,那么就将得票最少的城市淘汰掉,然后重复上述过程,直到选出一个申办城市为止.
(1)上述使用投票方式决定奥运会主办权的过程是算法吗?
(2)该算法若用程序框图来表示,只有顺序结构与条件结构可以吗?
(3)该算法中,控制重复操作的条件是什么?重复操作的内容是什么?
(4)什么是循环结构、循环体?提示(1)是.
(2)不可以.
(3)控制重复操作的条件为“是否有城市得票超过总票数的一半”,重复操作的内容是“淘汰得票最少的城市”.
(4)在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环体.2.做一做1:判断题
(1)循环结构中必然包含条件结构,以保证在适当的时候终止循环. ( )
(2)循环结构中,判断框内的条件不是唯一的. ( )
答案:(1)√ (2)√二、循环结构的形式
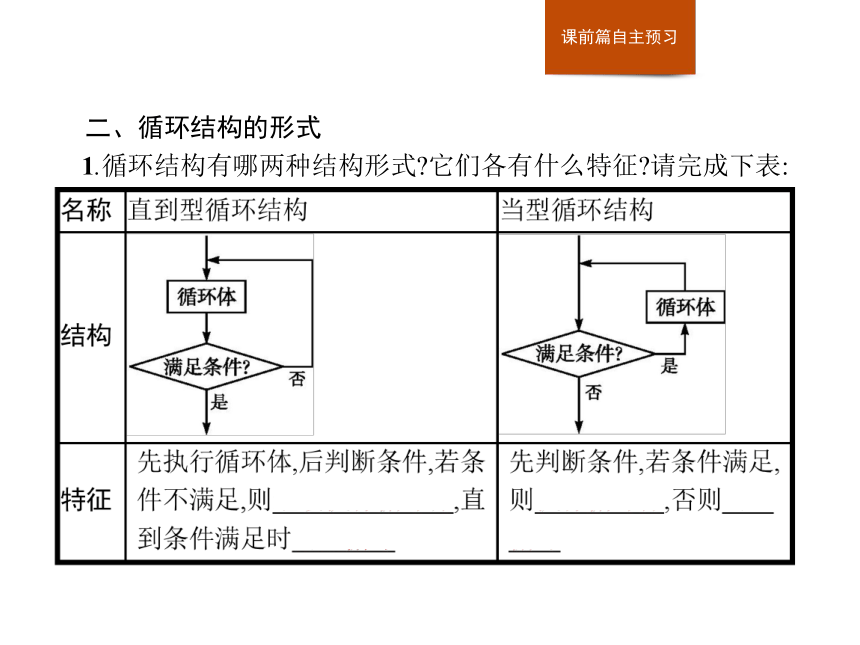
1.循环结构有哪两种结构形式?它们各有什么特征?请完成下表:2.做一做2:判断题
(1)当型循环结构中,只有满足条件时才执行循环体. ( )
(2)当型循环体和直到型循环体在执行时都至少要执行一次. ( )
(3)循环结构分为直到型循环结构和当型循环结构,两种结构不能相互转化. ( )
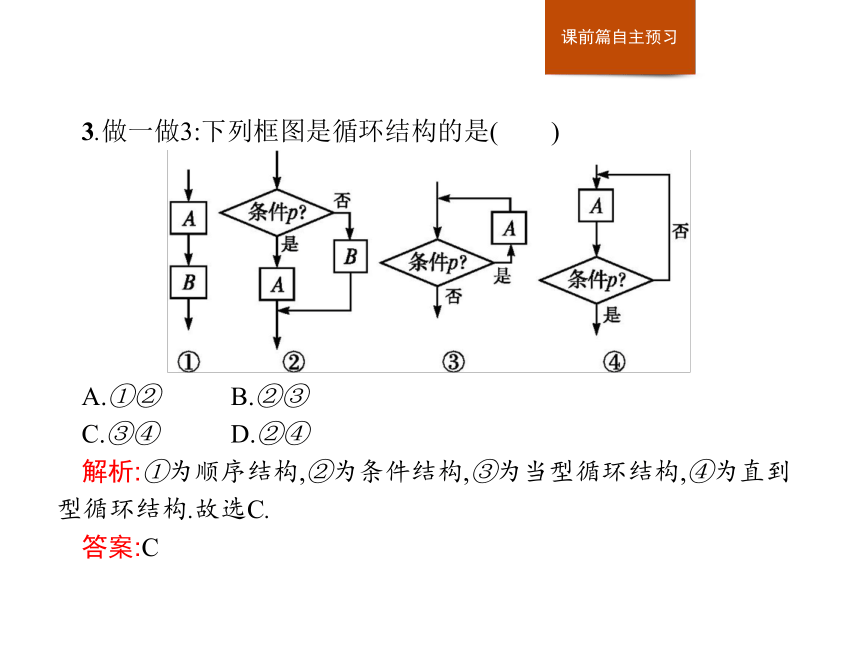
答案:(1)√ (2)× (3)×3.做一做3:下列框图是循环结构的是( )
A.①② B.②③
C.③④ D.②④
解析:①为顺序结构,②为条件结构,③为当型循环结构,④为直到型循环结构.故选C.
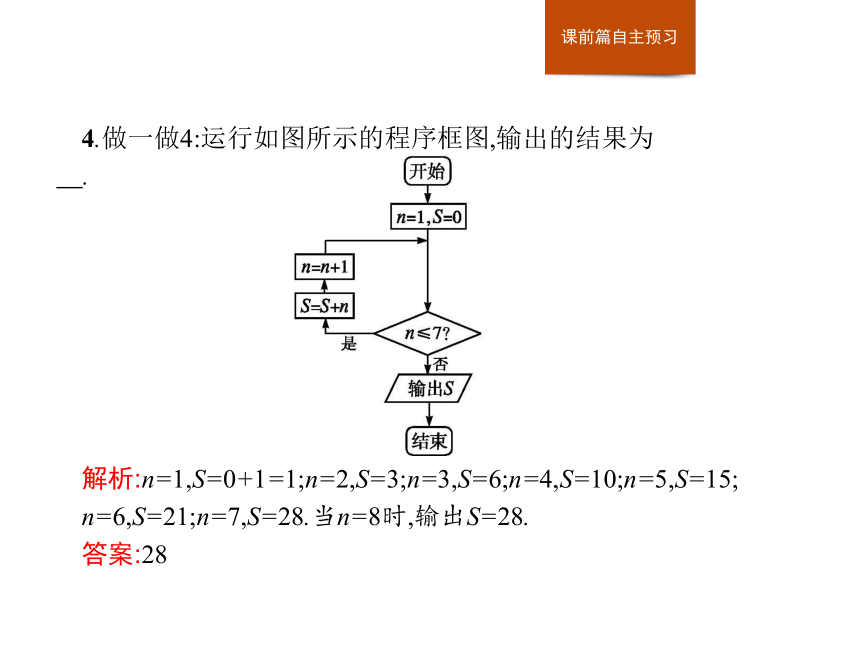
答案:C4.做一做4:运行如图所示的程序框图,输出的结果为 .?
解析:n=1,S=0+1=1;n=2,S=3;n=3,S=6;n=4,S=10;n=5,S=15;
n=6,S=21;n=7,S=28.当n=8时,输出S=28.
答案:28探究一探究二探究三思维辨析利用循环结构解决累加(乘)求值问题
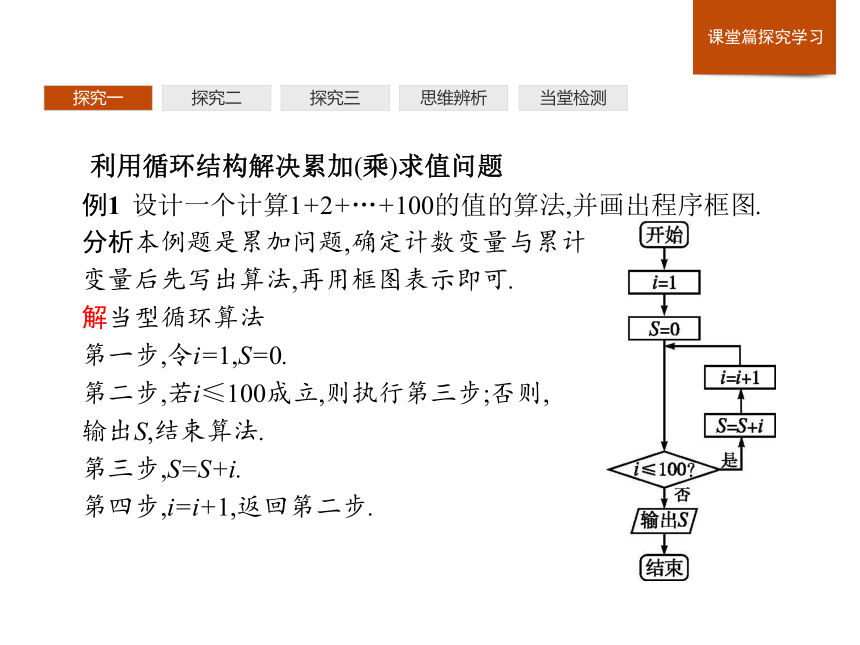
例1 设计一个计算1+2+…+100的值的算法,并画出程序框图.
分析本例题是累加问题,确定计数变量与累计
变量后先写出算法,再用框图表示即可.
解当型循环算法
第一步,令i=1,S=0.
第二步,若i≤100成立,则执行第三步;否则,
输出S,结束算法.
第三步,S=S+i.
第四步,i=i+1,返回第二步.当堂检测探究一探究二探究三思维辨析程序框图如右:
直到型循环算法:
第一步,令i=1,S=0.
第二步,S=S+i.
第三步,i=i+1.
第四步,若i>100不成立,则返回第二步;
否则,输出S,结束算法.
程序框图:当堂检测探究一探究二探究三思维辨析反思感悟1.若算法问题中涉及的运算进行了多次重复,且参与运算的数前后有规律可循,就可引入变量采用循环结构.
2.利用循环结构解决问题的三个关注点
(1)确定循环变量及初始值(累加变量的初始值一般为0,累乘变量的初始值一般为1);
(2)确定循环体(包括计数变量,累加(或累乘)变量);
(3)确定循环终止条件(表述要恰当,精确).当堂检测探究一探究二探究三思维辨析互动探究(1)若【例1】中的加法改为乘法,程序框图应怎样画?
(2)若【例1】中所求代数式换为2+4+6+…+100,试分别用当型和直到型循环结构画出算法流程图.
分析改为乘法之后,需要注意两个方面,S的起始值换为1;累计变量对应语句把加法改为乘法.当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析利用循环结构求满足条件的最大(小)整数问题
例2若1+3+5+…+n>2 019,试设计算法,并画出程序框图,寻找满足条件的最小奇数n.当堂检测探究一探究二探究三思维辨析解:算法分析:因为涉及累加问题,所以算法中需含有循环结构,算法步骤如下:
第一步,令S=0,n=1.
第二步,S=S+n,n=n+2.
第三步,判断S>2 019是否成立,若成立,则n=n-2,输出n;否则,返回第二步.
反思感悟 循环结构必包含顺序结构和条件结构,在累加、累乘等需要反复执行的算法设计中,宜使用循环结构,应用循环结构解决问题时,应特别注意两个变量(累加(或累乘)变量和计数变量)的初始值.另外,不要漏掉流程线的箭头及与判断框相连的流程线上的“是”或“否”.当堂检测探究一探究二探究三思维辨析循环结构的实际应用
例3 某工厂2019年生产小轿车200万辆,技术革新后预计每年的生产能力都比上一年增加5%,问最早哪一年该厂生产的小轿车数量超过300万辆?写出解决该问题的一个算法,并画出相应的程序框图.
分析该题中“每年的生产能力都比上一年增加5%”,显然是一个循环计数问题,首先建立数学模型——累乘问题中求满足不等式的最小整数问题,然后写出解决此类问题的算法,最后将其用框图表示出来即可.当堂检测探究一探究二探究三思维辨析解算法如下:
第一步,令n=0,a=200,r=0.05.
第二步,T=ar(计算年增量).
第三步,a=a+T(计算年产量).
第四步,如果a≤300,那么n=n+1,返回第二步;
否则执行第五步.
第五步,N=2 019+n.
第六步,输出N.
程序框图如图所示.当堂检测探究一探究二探究三思维辨析反思感悟利用循环结构解决实际问题的方法 当堂检测探究一探究二探究三思维辨析变式训练2以下是某次考试中某班15名同学的数学成绩(单位:分):72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来,画出解决该问题的算法的程序框图.
分析对于应用型问题,我们要根据数学实际问题的解题模式,认真审题,先建立数学模型,再结合实际要求和数学模型的特点,分析、设计相应的算法.当堂检测探究一探究二探究三思维辨析解程序框图如图所示. 当堂检测探究一探究二探究三思维辨析不能正确确定循环次数而致误
典例 设计一个算法,求1+2+4+…+249的值,并画出程序框图.
错解算法步骤:
第一步,令i=0,S=0.
第二步,S=S+2i.
第三步,i=i+1.
第四步,判断i是否大于等于49.若成立,
则输出S,结束算法;否则,返回第二步.
程序框图如图所示.当堂检测探究一探究二探究三思维辨析以上错解中都有哪些错误?出错的原因是什么?你如何订正?你如何防范?
错因分析在判断框中考虑是填写i>49还是填写i≥49时,关键是看i能否取到49.当i≥49时实际计算的是1+2+4+…+248的值.
正解算法步骤:
第一步,令i=0,S=0.
第二步,S=S+2i.
第三步,i=i+1.
第四步,判断i是否大于49.若成立,
则输出S,结束算法;否则,返回第二步.
程序框图如图所示.当堂检测探究一探究二探究三思维辨析防范措施1.循环结构中对循环次数的控制非常关键,它直接影响着运算的结果.
2.控制循环次数要引入循环变量,其取值如何限制,要弄清两个问题:一是需要运算的次数;二是循环结构的形式,是“当型”还是“直到型”.
3.要特别注意判断框中计数变量的取值限制,是“>”“<”,还是“≥”“≤”,它们的意义是不同的.当堂检测探究一探究二探究三思维辨析循环结束的条件判断不准致错
例2如图是一算法的程序框图,若此程序的输出结果为S=720,则判断框内可填入的条件是( )
A.k≥6?
B.k≥7?
C.k≥8?
D.k≥9?
错因分析本题容易出错的就是这个判断条件是什么,本题是当不满足判断框中的条件时结束循环,当满足判断框中的条件时执行循环,故应该从k=10开始按照递减的方式逐步到S的值为720时,结束循环,如果不清楚这个要求就可能误选选项B.当堂检测探究一探究二探究三思维辨析解析:第一次循环,S=10,k=9;第二次循环,S=10×9=90,k=8;第三次循环,S=720,k=7,由题意知,此时结束循环.这个程序中满足判断框的条件时执行循环,故判断条件是k≥8?.
答案:C
防范措施控制循环结构的是计数变量和累加(累乘)变量的变化规律以及循环结束的条件.在解答这类题目时首先要弄清楚这两个变量的变化规律,如本题中计数变量k从10开始逐一递减,累乘变量S从1开始逐步乘10,9,8;其次要看清楚循环结束的条件,这个条件由输出要求决定,如本题中就是要求当累乘变量的值为720时结束循环,同时应看清楚是满足条件时结束循环还是不满足条件时结束循环.当堂检测探究一探究二探究三思维辨析当堂检测1.关于如图所示的两个程序框图,说法正确的是( )
A.图(1)(2)都是顺序结构
B.图(1)(2)都是条件结构
C.图(1)是当型循环结构,图(2)是直到型循环结构
D.图(1)是直到型循环结构,图(2)是当型循环结构
解析:观察图(1),它是先判断后循环,故是当型循环结构;观察图(2),它是先循环后判断,故是直到型循环结构.
答案:C探究一探究二探究三思维辨析当堂检测2.如图所示的算法程序框图,则输出的表达式为( )
解析:当i=99时满足i<100,此时S=1+2+3+…+99,当i=100时,不满足i<100,所以输出
答案:A探究一探究二探究三思维辨析当堂检测3.如图所示的程序框图的输出值y∈(1,2],则输入值x∈ ( )
A.[-log23,-1)∪(1,3)
B.(-1,-log32]∪[1,2)
C.[-log23,-1)∪(1,3]
D.(-1,-log32]∪(1,2]
解析:当x≥0时,y=log2(x+1),由y∈(1,2]有1答案:C探究一探究二探究三思维辨析当堂检测4.执行如图所示的程序框图,输出的S值为 .?
解析:k=0<3,S=1,S=1×20=1;
k=0+1=1<3,S=1×21=2;
k=1+1=2<3,S=2×22=8;
k=2+1=3,跳出循环,输出S=8.
答案:8
1.在申办奥运会的最后阶段,你知道国际奥委会是如何通过投票决定主办权归属的吗?对竞选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票数超过总票数的一半,那么该城市就获得主办权;如果所有申办城市得票数都不超过总票数的一半,那么就将得票最少的城市淘汰掉,然后重复上述过程,直到选出一个申办城市为止.
(1)上述使用投票方式决定奥运会主办权的过程是算法吗?
(2)该算法若用程序框图来表示,只有顺序结构与条件结构可以吗?
(3)该算法中,控制重复操作的条件是什么?重复操作的内容是什么?
(4)什么是循环结构、循环体?提示(1)是.
(2)不可以.
(3)控制重复操作的条件为“是否有城市得票超过总票数的一半”,重复操作的内容是“淘汰得票最少的城市”.
(4)在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.反复执行的步骤称为循环体.2.做一做1:判断题
(1)循环结构中必然包含条件结构,以保证在适当的时候终止循环. ( )
(2)循环结构中,判断框内的条件不是唯一的. ( )
答案:(1)√ (2)√二、循环结构的形式
1.循环结构有哪两种结构形式?它们各有什么特征?请完成下表:2.做一做2:判断题
(1)当型循环结构中,只有满足条件时才执行循环体. ( )
(2)当型循环体和直到型循环体在执行时都至少要执行一次. ( )
(3)循环结构分为直到型循环结构和当型循环结构,两种结构不能相互转化. ( )
答案:(1)√ (2)× (3)×3.做一做3:下列框图是循环结构的是( )
A.①② B.②③
C.③④ D.②④
解析:①为顺序结构,②为条件结构,③为当型循环结构,④为直到型循环结构.故选C.
答案:C4.做一做4:运行如图所示的程序框图,输出的结果为 .?
解析:n=1,S=0+1=1;n=2,S=3;n=3,S=6;n=4,S=10;n=5,S=15;
n=6,S=21;n=7,S=28.当n=8时,输出S=28.
答案:28探究一探究二探究三思维辨析利用循环结构解决累加(乘)求值问题
例1 设计一个计算1+2+…+100的值的算法,并画出程序框图.
分析本例题是累加问题,确定计数变量与累计
变量后先写出算法,再用框图表示即可.
解当型循环算法
第一步,令i=1,S=0.
第二步,若i≤100成立,则执行第三步;否则,
输出S,结束算法.
第三步,S=S+i.
第四步,i=i+1,返回第二步.当堂检测探究一探究二探究三思维辨析程序框图如右:
直到型循环算法:
第一步,令i=1,S=0.
第二步,S=S+i.
第三步,i=i+1.
第四步,若i>100不成立,则返回第二步;
否则,输出S,结束算法.
程序框图:当堂检测探究一探究二探究三思维辨析反思感悟1.若算法问题中涉及的运算进行了多次重复,且参与运算的数前后有规律可循,就可引入变量采用循环结构.
2.利用循环结构解决问题的三个关注点
(1)确定循环变量及初始值(累加变量的初始值一般为0,累乘变量的初始值一般为1);
(2)确定循环体(包括计数变量,累加(或累乘)变量);
(3)确定循环终止条件(表述要恰当,精确).当堂检测探究一探究二探究三思维辨析互动探究(1)若【例1】中的加法改为乘法,程序框图应怎样画?
(2)若【例1】中所求代数式换为2+4+6+…+100,试分别用当型和直到型循环结构画出算法流程图.
分析改为乘法之后,需要注意两个方面,S的起始值换为1;累计变量对应语句把加法改为乘法.当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析当堂检测探究一探究二探究三思维辨析利用循环结构求满足条件的最大(小)整数问题
例2若1+3+5+…+n>2 019,试设计算法,并画出程序框图,寻找满足条件的最小奇数n.当堂检测探究一探究二探究三思维辨析解:算法分析:因为涉及累加问题,所以算法中需含有循环结构,算法步骤如下:
第一步,令S=0,n=1.
第二步,S=S+n,n=n+2.
第三步,判断S>2 019是否成立,若成立,则n=n-2,输出n;否则,返回第二步.
反思感悟 循环结构必包含顺序结构和条件结构,在累加、累乘等需要反复执行的算法设计中,宜使用循环结构,应用循环结构解决问题时,应特别注意两个变量(累加(或累乘)变量和计数变量)的初始值.另外,不要漏掉流程线的箭头及与判断框相连的流程线上的“是”或“否”.当堂检测探究一探究二探究三思维辨析循环结构的实际应用
例3 某工厂2019年生产小轿车200万辆,技术革新后预计每年的生产能力都比上一年增加5%,问最早哪一年该厂生产的小轿车数量超过300万辆?写出解决该问题的一个算法,并画出相应的程序框图.
分析该题中“每年的生产能力都比上一年增加5%”,显然是一个循环计数问题,首先建立数学模型——累乘问题中求满足不等式的最小整数问题,然后写出解决此类问题的算法,最后将其用框图表示出来即可.当堂检测探究一探究二探究三思维辨析解算法如下:
第一步,令n=0,a=200,r=0.05.
第二步,T=ar(计算年增量).
第三步,a=a+T(计算年产量).
第四步,如果a≤300,那么n=n+1,返回第二步;
否则执行第五步.
第五步,N=2 019+n.
第六步,输出N.
程序框图如图所示.当堂检测探究一探究二探究三思维辨析反思感悟利用循环结构解决实际问题的方法 当堂检测探究一探究二探究三思维辨析变式训练2以下是某次考试中某班15名同学的数学成绩(单位:分):72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来,画出解决该问题的算法的程序框图.
分析对于应用型问题,我们要根据数学实际问题的解题模式,认真审题,先建立数学模型,再结合实际要求和数学模型的特点,分析、设计相应的算法.当堂检测探究一探究二探究三思维辨析解程序框图如图所示. 当堂检测探究一探究二探究三思维辨析不能正确确定循环次数而致误
典例 设计一个算法,求1+2+4+…+249的值,并画出程序框图.
错解算法步骤:
第一步,令i=0,S=0.
第二步,S=S+2i.
第三步,i=i+1.
第四步,判断i是否大于等于49.若成立,
则输出S,结束算法;否则,返回第二步.
程序框图如图所示.当堂检测探究一探究二探究三思维辨析以上错解中都有哪些错误?出错的原因是什么?你如何订正?你如何防范?
错因分析在判断框中考虑是填写i>49还是填写i≥49时,关键是看i能否取到49.当i≥49时实际计算的是1+2+4+…+248的值.
正解算法步骤:
第一步,令i=0,S=0.
第二步,S=S+2i.
第三步,i=i+1.
第四步,判断i是否大于49.若成立,
则输出S,结束算法;否则,返回第二步.
程序框图如图所示.当堂检测探究一探究二探究三思维辨析防范措施1.循环结构中对循环次数的控制非常关键,它直接影响着运算的结果.
2.控制循环次数要引入循环变量,其取值如何限制,要弄清两个问题:一是需要运算的次数;二是循环结构的形式,是“当型”还是“直到型”.
3.要特别注意判断框中计数变量的取值限制,是“>”“<”,还是“≥”“≤”,它们的意义是不同的.当堂检测探究一探究二探究三思维辨析循环结束的条件判断不准致错
例2如图是一算法的程序框图,若此程序的输出结果为S=720,则判断框内可填入的条件是( )
A.k≥6?
B.k≥7?
C.k≥8?
D.k≥9?
错因分析本题容易出错的就是这个判断条件是什么,本题是当不满足判断框中的条件时结束循环,当满足判断框中的条件时执行循环,故应该从k=10开始按照递减的方式逐步到S的值为720时,结束循环,如果不清楚这个要求就可能误选选项B.当堂检测探究一探究二探究三思维辨析解析:第一次循环,S=10,k=9;第二次循环,S=10×9=90,k=8;第三次循环,S=720,k=7,由题意知,此时结束循环.这个程序中满足判断框的条件时执行循环,故判断条件是k≥8?.
答案:C
防范措施控制循环结构的是计数变量和累加(累乘)变量的变化规律以及循环结束的条件.在解答这类题目时首先要弄清楚这两个变量的变化规律,如本题中计数变量k从10开始逐一递减,累乘变量S从1开始逐步乘10,9,8;其次要看清楚循环结束的条件,这个条件由输出要求决定,如本题中就是要求当累乘变量的值为720时结束循环,同时应看清楚是满足条件时结束循环还是不满足条件时结束循环.当堂检测探究一探究二探究三思维辨析当堂检测1.关于如图所示的两个程序框图,说法正确的是( )
A.图(1)(2)都是顺序结构
B.图(1)(2)都是条件结构
C.图(1)是当型循环结构,图(2)是直到型循环结构
D.图(1)是直到型循环结构,图(2)是当型循环结构
解析:观察图(1),它是先判断后循环,故是当型循环结构;观察图(2),它是先循环后判断,故是直到型循环结构.
答案:C探究一探究二探究三思维辨析当堂检测2.如图所示的算法程序框图,则输出的表达式为( )
解析:当i=99时满足i<100,此时S=1+2+3+…+99,当i=100时,不满足i<100,所以输出
答案:A探究一探究二探究三思维辨析当堂检测3.如图所示的程序框图的输出值y∈(1,2],则输入值x∈ ( )
A.[-log23,-1)∪(1,3)
B.(-1,-log32]∪[1,2)
C.[-log23,-1)∪(1,3]
D.(-1,-log32]∪(1,2]
解析:当x≥0时,y=log2(x+1),由y∈(1,2]有1
解析:k=0<3,S=1,S=1×20=1;
k=0+1=1<3,S=1×21=2;
k=1+1=2<3,S=2×22=8;
k=2+1=3,跳出循环,输出S=8.
答案:8
