高中数学人教A版必修三课件 1章 模块复习课 第1课时 算法初步 :39张PPT
文档属性
| 名称 | 高中数学人教A版必修三课件 1章 模块复习课 第1课时 算法初步 :39张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:21:38 | ||
图片预览









文档简介
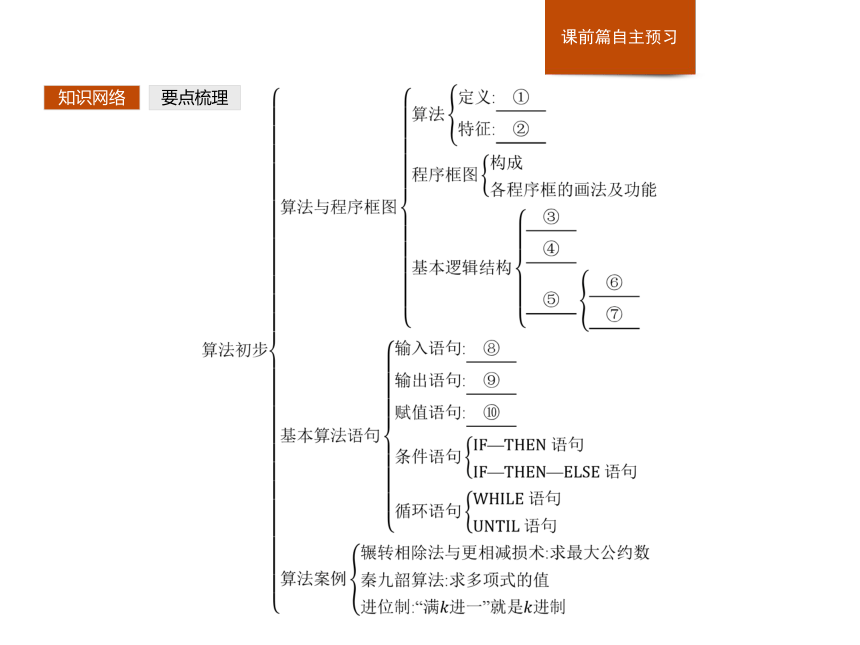
课件39张PPT。第1课时 算法初步知识网络要点梳理知识网络填一填:①?
②?
③ ④ ⑤ ?
⑥ ?
⑦ ?
⑧?
⑨?
⑩ ?
答案:①通常是指按照一定的规则解决某一类问题的明确和有限的步骤 ②有限性、确定性、可行性、有序性、普遍性、不唯一性 ③顺序结构 ④条件结构 ⑤循环结构 ⑥直到型循环结构 ⑦当型循环结构 ⑧INPUT “提示内容”;变量 ⑨PRINT “提示内容”;表达式 ⑩变量=表达式要点梳理知识网络要点梳理1.什么是算法?
提示算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.
2.什么是程序框图?
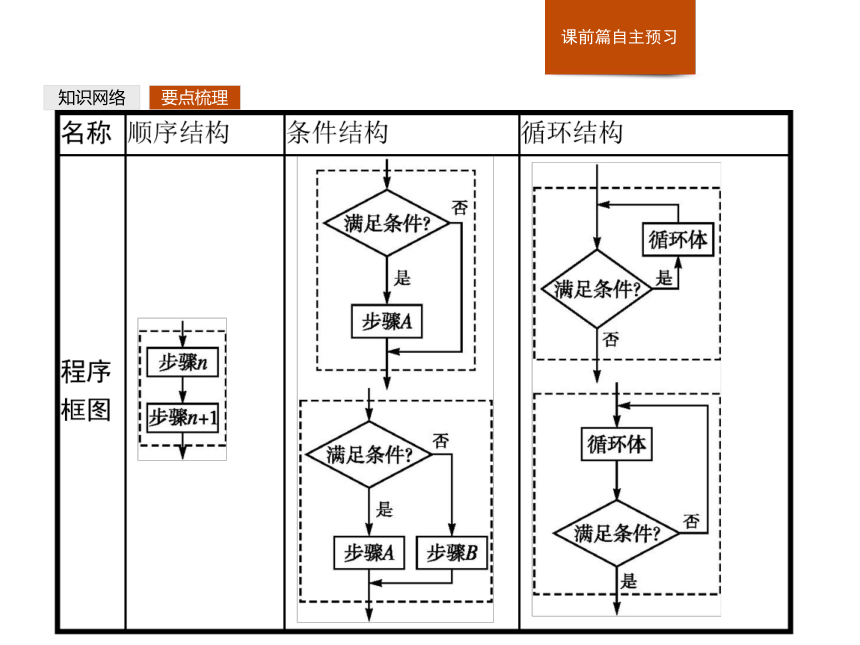
提示程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.知识网络要点梳理3.关于算法的三种基本逻辑结构,请完成下表: 知识网络要点梳理知识网络要点梳理4.填空:三种算法语句的格式与应用
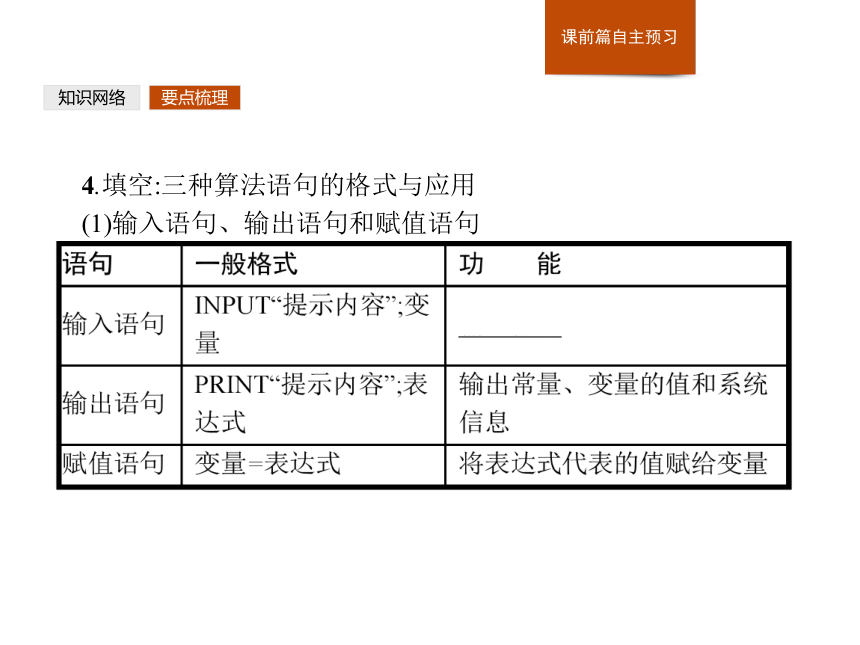
(1)输入语句、输出语句和赋值语句知识网络要点梳理(2)条件语句
①功能:实现条件结构.
②条件语句的格式及框图:
a.IF-THEN格式
IF 条件 THEN
语句体
END IF
b.IF-THEN-ELSE格式
IF 条件 THEN
语句体1
ELSE
语句体2
END IF知识网络(3)循环语句
①功能:实现程序框图中的循环结构.
②循环语句的格式及框图:
a.UNTIL语句
DO
循环体
LOOP UNTIL条件
b.WHILE语句
WHILE条件
循环体
WEND要点梳理知识网络思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)算法只能解决一个问题,不能重复使用.( )
(2)算法可以无限操作下去.( )
(3)程序框图中的图形符号可以由个人来确定.( )
(4)输入框只能紧接开始框,输出框只能紧接结束框.( )
(5) 是赋值框,有计算功能.( )
(6)一个程序框图可以只有顺序结构.( )
(7)条件结构的出口有两个,但在执行时,只有一个出口是有效的.( )要点梳理知识网络(8)任何算法必有条件结构.( )
(9)条件结构中还可以包含条件结构.( )
(10)“当型”循环和“直到型”循环都是在条件满足时,退出循环.( )
(11)输入语句可以给多个变量同时赋值.( )
(12)在算法语句中,X=X+1是错误的.( )
答案:(1)× (2)× (3)× (4)× (5)× (6)√
(7)√ (8)× (9)√ (10)× (11)√ (12)×要点梳理专题归纳高考体验专题一 算法设计
算法设计的一般步骤
算法设计与一般意义上的解决问题既有区别又有联系,它是某类问题一般解法的抽象与概括,它要借助问题的一般解决方法.一般步骤为:
(1)认真分析所给的问题,找出解决该类问题的一般方法.
(2)借助变量或参数对算法进行描述.
(3)将解决问题的过程分解为若干个可执行的步骤.
(4)用简洁的语言将各个步骤表述出来.专题归纳高考体验 【例1 已知平面直角坐标系中的两点A(-1,0),B(3,2),写出求线段AB的垂直平分线方程的一个算法.专题归纳高考体验跟踪训练写出求方程x2-4x-12=0的根的一个算法.
解法一第一步,移项,得x2-4x=12.①
第二步,①式两边同加4并配方,得(x-2)2=16.②
第三步,②式两边开方,得x-2=±4.③
第四步,解:③得x=6或x=-2.
解法二第一步,将方程左边因式分解,
得(x-6)(x+2)=0.①
第二步,由①得x-6=0或x+2=0.②
第三步,解:②得x=6或x=-2.
解法三第一步,计算方程的判别式Δ=42+4×12>0.
第二步,将a=1,b=-4,c=-12代入求根公式专题归纳高考体验专题二 程序框图的应用
程序框图是用规定的图形和流程线来准确、直观、形象地表示算法的图形.画程序框图之前应首先对问题设计出合理有效的算法,然后分析算法的逻辑结构,画出相应的程序框图,算法的逻辑结构有三种:顺序结构、条件结构和循环结构.
①条件结构是一种重要的选择结构.比如比较两个数的大小、对一组数进行排序筛选等问题都要用到条件结构.②在利用循环结构画程序框图前,要确定三件事:一是确定循环变量的初始条件;二是确定算法中反复执行的部分,即循环体;三是循环终止的条件.专题归纳高考体验第三步,i=i+1.
第四步,若i>6,则输出x,结束算法;否则,
返回第二步,重新执行第二步,第三步.
相应算法的程序框图如图所示.专题归纳高考体验专题三 用基本算法语句编写程序
算法设计和程序框图是设计程序的基础.编写程序的基本方法是“自上而下逐步求解”,步骤如下:
(1)把一个复杂的大问题分解成若干相对独立的小问题.若小问题仍较复杂,则可以把小问题分解成若干个子问题.这样不断地分解,使小问题或子问题简单到能直接用程序的三种基本结构甚至是五种基本语句表达清楚为止.(2)对应每一个小问题或子问题编写出一个功能相对独立的程序块来.(3)把每一个模块统一组装,完成程序.专题归纳高考体验S=0
i=1
WHILE ?
?
?
?
PRINT S
END专题归纳高考体验解:
S=0
i=1
WHILE i<=99
S=S+1/(i*(i+2))?
i=i+2 ?
WEND ?
PRINT S
END专题归纳高考体验互动探究对本例,请设计另一种循环结构的程序.
解:用UNTIL语句编写程序如下:
S=0
i=1
DO
S=S+1/(i*(i+2))
i=i+2
LOOP UNTIL i>99
PRINT S
END专题归纳高考体验专题四 算法案例
算法案例包含三方面的内容:辗转相除法与更相减损术、秦九韶算法、进位制.利用辗转相除法或更相减损术可以求两个正整数的最大公约数;利用秦九韶算法可以求多项式的值,利用进位制的知识可以进行进位制之间的转化.
例4 354与1 357的最大公约数是 .?
解析:因为1 357=354×3+295,
354=295×1+59,
295=59×5,
所以59是354与1 357的最大公约数.
答案:59专题归纳高考体验反思归纳求两个正整数的最大公约数可以采用辗转相除法或更相减损术,如果求三个正整数的最大公约数,那么应先求两个数的最大公约数,再求这个最大公约数与第三个数的最大公约数.专题归纳高考体验例5 用秦九韶算法求多项式f(x)=4x5+3x4+5x3+x2+x当x=2时的值.
解:因为f(x)=((((4x+3)x+5)x+1)x+1)x,
所以v0=4,v1=4×2+3=11,v2=11×2+5=27,
v3=27×2+1=55,v4=55×2+1=111,
v5=111×2=222.
所以当x=2时,多项式f(x)=4x5+3x4+5x3+x2+x的值为222.专题归纳高考体验反思归纳可把f(x)=anxn+an-1xn-1+…+a1x+a0的值转化为递推公式:
需运算的乘法次数为n,加法次数为n,共需运算的次数为2n.可见,在求f(x)=anxn+an-1xn-1+…+a1x+a0的值的算法中,秦九韶算法将直接求解的 次运算降为2n次运算,在这个方面秦九韶算法比其他算法优越得多.专题归纳高考体验例6 (1)将七进制数235(7)转化为十进制数;
(2)将五进制数44(5)转化为二进制数.
解:(1)235(7)=2×72+3×71+5×70=124.
(2)44(5)=4×51+4×50=24,
所以24=11000(2),即44(5)=11000(2).
反思归纳进制数的转化一般以十进制数为桥梁,先把其他进制数转化为十进制数,再进行转化,特别注意不要忘掉表示进制的基数.专题归纳高考体验考点一:条件结构 专题归纳高考体验答案:A 专题归纳高考体验2.(2019全国3高考)执行下边的程序框图,如果输入的ε为0.01,则输出s的值等于( )专题归纳高考体验答案:C 专题归纳高考体验考点二:循环结构
3.(2019天津高考)阅读下边的程序框图,运行相应的程序,输出S的值为( )
A.5 B.8
C.24 D.29专题归纳高考体验解析:i=1,为奇数,S=1;
i=2,为偶数,S=1+2×21=5;
i=3,为奇数,S=8;
i=4,此时4≥4,满足要求,输出S=8.
故选B.
答案:B专题归纳高考体验4.(2018全国2高考)为计算 设计了下面的程序框图,则在空白框中应填入 ( )
A.i=i+1
B.i=i+2
C.i=i+3
D.i=i+4专题归纳高考体验答案:B 专题归纳高考体验5.(2017全国3高考)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5
B.4
C.3
D.2专题归纳高考体验解析:程序运行过程如下表所示:
此时S=90<91首次满足条件,程序需在t=3时跳出循环,即N=2为满足条件的最小值,故选D.
答案:D专题归纳高考体验6.(2017全国1高考)下面程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在
A.A>1 000?和n=n+1
B.A>1 000?和n=n+2
C.A≤1 000?和n=n+1
D.A≤1 000?和n=n+2专题归纳高考体验答案:D 专题归纳高考体验7.(2019江苏高考)下图是一个算法流程图,则输出的S的值是 .?专题归纳高考体验答案:5
②?
③ ④ ⑤ ?
⑥ ?
⑦ ?
⑧?
⑨?
⑩ ?
答案:①通常是指按照一定的规则解决某一类问题的明确和有限的步骤 ②有限性、确定性、可行性、有序性、普遍性、不唯一性 ③顺序结构 ④条件结构 ⑤循环结构 ⑥直到型循环结构 ⑦当型循环结构 ⑧INPUT “提示内容”;变量 ⑨PRINT “提示内容”;表达式 ⑩变量=表达式要点梳理知识网络要点梳理1.什么是算法?
提示算法通常是指按照一定规则解决某一类问题的明确和有限的步骤.
2.什么是程序框图?
提示程序框图又称流程图,是一种用程序框、流程线及文字说明来表示算法的图形.知识网络要点梳理3.关于算法的三种基本逻辑结构,请完成下表: 知识网络要点梳理知识网络要点梳理4.填空:三种算法语句的格式与应用
(1)输入语句、输出语句和赋值语句知识网络要点梳理(2)条件语句
①功能:实现条件结构.
②条件语句的格式及框图:
a.IF-THEN格式
IF 条件 THEN
语句体
END IF
b.IF-THEN-ELSE格式
IF 条件 THEN
语句体1
ELSE
语句体2
END IF知识网络(3)循环语句
①功能:实现程序框图中的循环结构.
②循环语句的格式及框图:
a.UNTIL语句
DO
循环体
LOOP UNTIL条件
b.WHILE语句
WHILE条件
循环体
WEND要点梳理知识网络思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)算法只能解决一个问题,不能重复使用.( )
(2)算法可以无限操作下去.( )
(3)程序框图中的图形符号可以由个人来确定.( )
(4)输入框只能紧接开始框,输出框只能紧接结束框.( )
(5) 是赋值框,有计算功能.( )
(6)一个程序框图可以只有顺序结构.( )
(7)条件结构的出口有两个,但在执行时,只有一个出口是有效的.( )要点梳理知识网络(8)任何算法必有条件结构.( )
(9)条件结构中还可以包含条件结构.( )
(10)“当型”循环和“直到型”循环都是在条件满足时,退出循环.( )
(11)输入语句可以给多个变量同时赋值.( )
(12)在算法语句中,X=X+1是错误的.( )
答案:(1)× (2)× (3)× (4)× (5)× (6)√
(7)√ (8)× (9)√ (10)× (11)√ (12)×要点梳理专题归纳高考体验专题一 算法设计
算法设计的一般步骤
算法设计与一般意义上的解决问题既有区别又有联系,它是某类问题一般解法的抽象与概括,它要借助问题的一般解决方法.一般步骤为:
(1)认真分析所给的问题,找出解决该类问题的一般方法.
(2)借助变量或参数对算法进行描述.
(3)将解决问题的过程分解为若干个可执行的步骤.
(4)用简洁的语言将各个步骤表述出来.专题归纳高考体验 【例1 已知平面直角坐标系中的两点A(-1,0),B(3,2),写出求线段AB的垂直平分线方程的一个算法.专题归纳高考体验跟踪训练写出求方程x2-4x-12=0的根的一个算法.
解法一第一步,移项,得x2-4x=12.①
第二步,①式两边同加4并配方,得(x-2)2=16.②
第三步,②式两边开方,得x-2=±4.③
第四步,解:③得x=6或x=-2.
解法二第一步,将方程左边因式分解,
得(x-6)(x+2)=0.①
第二步,由①得x-6=0或x+2=0.②
第三步,解:②得x=6或x=-2.
解法三第一步,计算方程的判别式Δ=42+4×12>0.
第二步,将a=1,b=-4,c=-12代入求根公式专题归纳高考体验专题二 程序框图的应用
程序框图是用规定的图形和流程线来准确、直观、形象地表示算法的图形.画程序框图之前应首先对问题设计出合理有效的算法,然后分析算法的逻辑结构,画出相应的程序框图,算法的逻辑结构有三种:顺序结构、条件结构和循环结构.
①条件结构是一种重要的选择结构.比如比较两个数的大小、对一组数进行排序筛选等问题都要用到条件结构.②在利用循环结构画程序框图前,要确定三件事:一是确定循环变量的初始条件;二是确定算法中反复执行的部分,即循环体;三是循环终止的条件.专题归纳高考体验第三步,i=i+1.
第四步,若i>6,则输出x,结束算法;否则,
返回第二步,重新执行第二步,第三步.
相应算法的程序框图如图所示.专题归纳高考体验专题三 用基本算法语句编写程序
算法设计和程序框图是设计程序的基础.编写程序的基本方法是“自上而下逐步求解”,步骤如下:
(1)把一个复杂的大问题分解成若干相对独立的小问题.若小问题仍较复杂,则可以把小问题分解成若干个子问题.这样不断地分解,使小问题或子问题简单到能直接用程序的三种基本结构甚至是五种基本语句表达清楚为止.(2)对应每一个小问题或子问题编写出一个功能相对独立的程序块来.(3)把每一个模块统一组装,完成程序.专题归纳高考体验S=0
i=1
WHILE ?
?
?
?
PRINT S
END专题归纳高考体验解:
S=0
i=1
WHILE i<=99
S=S+1/(i*(i+2))?
i=i+2 ?
WEND ?
PRINT S
END专题归纳高考体验互动探究对本例,请设计另一种循环结构的程序.
解:用UNTIL语句编写程序如下:
S=0
i=1
DO
S=S+1/(i*(i+2))
i=i+2
LOOP UNTIL i>99
PRINT S
END专题归纳高考体验专题四 算法案例
算法案例包含三方面的内容:辗转相除法与更相减损术、秦九韶算法、进位制.利用辗转相除法或更相减损术可以求两个正整数的最大公约数;利用秦九韶算法可以求多项式的值,利用进位制的知识可以进行进位制之间的转化.
例4 354与1 357的最大公约数是 .?
解析:因为1 357=354×3+295,
354=295×1+59,
295=59×5,
所以59是354与1 357的最大公约数.
答案:59专题归纳高考体验反思归纳求两个正整数的最大公约数可以采用辗转相除法或更相减损术,如果求三个正整数的最大公约数,那么应先求两个数的最大公约数,再求这个最大公约数与第三个数的最大公约数.专题归纳高考体验例5 用秦九韶算法求多项式f(x)=4x5+3x4+5x3+x2+x当x=2时的值.
解:因为f(x)=((((4x+3)x+5)x+1)x+1)x,
所以v0=4,v1=4×2+3=11,v2=11×2+5=27,
v3=27×2+1=55,v4=55×2+1=111,
v5=111×2=222.
所以当x=2时,多项式f(x)=4x5+3x4+5x3+x2+x的值为222.专题归纳高考体验反思归纳可把f(x)=anxn+an-1xn-1+…+a1x+a0的值转化为递推公式:
需运算的乘法次数为n,加法次数为n,共需运算的次数为2n.可见,在求f(x)=anxn+an-1xn-1+…+a1x+a0的值的算法中,秦九韶算法将直接求解的 次运算降为2n次运算,在这个方面秦九韶算法比其他算法优越得多.专题归纳高考体验例6 (1)将七进制数235(7)转化为十进制数;
(2)将五进制数44(5)转化为二进制数.
解:(1)235(7)=2×72+3×71+5×70=124.
(2)44(5)=4×51+4×50=24,
所以24=11000(2),即44(5)=11000(2).
反思归纳进制数的转化一般以十进制数为桥梁,先把其他进制数转化为十进制数,再进行转化,特别注意不要忘掉表示进制的基数.专题归纳高考体验考点一:条件结构 专题归纳高考体验答案:A 专题归纳高考体验2.(2019全国3高考)执行下边的程序框图,如果输入的ε为0.01,则输出s的值等于( )专题归纳高考体验答案:C 专题归纳高考体验考点二:循环结构
3.(2019天津高考)阅读下边的程序框图,运行相应的程序,输出S的值为( )
A.5 B.8
C.24 D.29专题归纳高考体验解析:i=1,为奇数,S=1;
i=2,为偶数,S=1+2×21=5;
i=3,为奇数,S=8;
i=4,此时4≥4,满足要求,输出S=8.
故选B.
答案:B专题归纳高考体验4.(2018全国2高考)为计算 设计了下面的程序框图,则在空白框中应填入 ( )
A.i=i+1
B.i=i+2
C.i=i+3
D.i=i+4专题归纳高考体验答案:B 专题归纳高考体验5.(2017全国3高考)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
A.5
B.4
C.3
D.2专题归纳高考体验解析:程序运行过程如下表所示:
此时S=90<91首次满足条件,程序需在t=3时跳出循环,即N=2为满足条件的最小值,故选D.
答案:D专题归纳高考体验6.(2017全国1高考)下面程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在
A.A>1 000?和n=n+1
B.A>1 000?和n=n+2
C.A≤1 000?和n=n+1
D.A≤1 000?和n=n+2专题归纳高考体验答案:D 专题归纳高考体验7.(2019江苏高考)下图是一个算法流程图,则输出的S的值是 .?专题归纳高考体验答案:5
