高中数学人教A版必修三课件 3.1.2 概率的意义 :30张PPT
文档属性
| 名称 | 高中数学人教A版必修三课件 3.1.2 概率的意义 :30张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 631.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:24:01 | ||
图片预览











文档简介
课件30张PPT。3.1.2 概率的意义一、对概率的正确理解
1.有人说,既然抛掷一枚质地均匀的硬币出现正面朝上的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种说法正确吗?
提示这种说法是错误的,抛掷一枚质地均匀的硬币出现正面朝上的概率为0.5,它是大量试验得出的一种规律性结果,对具体的几次试验来讲不一定能体现出这种规律性,在连续抛掷一枚质地均匀的硬币两次的试验中,可能两次均正面朝上,也可能两次均反面朝上,也可能一次正面朝上,一次反面朝上.2.若某种彩票准备发行1 000万张,其中有1万张可以中奖,则买一张这种彩票的中奖概率是多少?买1 000张的话是否一定会中奖?3.填空:随机事件在一次试验中发生与否是随机的,但随机性中含有规律性,认识了这种随机性中的规律性,就能比较准确地预测随机事件发生的可能性.
4.做一做1:掷一枚均匀的硬币,正面向上的概率是 ,那么在掷一百次试验中,正面向上的次数是( )
A.50 B.大于50 C.小于50 D.大约50
答案:D二、游戏的公平性
1.甲、乙两人做游戏,从装有3个白球1个黑球的袋子中任取1球,如果是白球,甲胜;否则,乙胜.试问这个游戏对两个人来说公平吗?谁获胜的机会大一些?
提示不公平.甲获胜的机会大一些.
2.在乒乓球比赛前,要决定由谁先发球.裁判员拿出一个抽签器(一个像大硬币似的均匀塑料圆板,一面是红圈,一面是绿圈),然后随意指定一名运动员,要他猜上抛的抽签器落到球台上时,是红圈那面朝上还是绿圈那面朝上.如果他猜对了,就由他先发球,否则,由另一方先发球.你认为公平吗?为什么?
提示公平.因为当抽签器上抛后,红圈朝上与绿圈朝上的概率都是0.5,因此任何一名运动员猜中的概率都是0.5,也就是每个运动员取得发球权的概率均为0.5,所以这个规则是公平的.3.填空:在设计某种游戏规则时,一定要考虑这种规则对每个人都是公平的这一重要原则.
三、决策中的概率思想
1.如果连续10次掷一枚骰子,结果都是出现1点,你认为这枚骰子的质地均匀吗?为什么?
提示可以推测这枚骰子的质地不均匀,并且很有可能是标有6点的那面比较重,使得出现1点的概率最大,才会连续10次都出现1点.2.填空:如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法.极大似然法是统计中重要的统计思想方法之一.
3.做一做2:如果掷一枚硬币100次,结果只有2次正面向上,如果只考虑硬币是否均匀,我们的判断是 .?
答案:硬币是不均匀的四、天气预报的概率解释
1.“昨天没有下雨,而天气预报说昨天降水的概率为90%.这说明预报是错误的”这种说法科学吗?
提示不科学.
2.填空:天气预报的“降水”是一个随机事件,“概率为90%”指明了“降水”这个随机事件发生的概率为90%.在一次试验中,概率为90%的事件也可能不出现.因此,“昨天没有下雨”并不能说明“昨天的降水概率为90%”的天气预报是错误的.五、试验与发现、遗传机理中的统计规律
1.奥地利遗传学家孟德尔1856年开始用豌豆作试验,他把黄色和绿色的豌豆杂交,第一年收获的豌豆都是黄色的.第二年,当他把第一年收获的黄色豌豆再种下时,收获的豌豆既有黄色的又有绿色的.同样他把圆形和皱皮豌豆杂交,第一年收获的豌豆都是圆形的.第二年,当他把第一年收获的圆形豌豆再种下时,收获的却既有圆形豌豆,又有皱皮豌豆.类似地,他把长茎的豌豆与短茎的豌豆杂交,第一年长出来的都是长茎的豌豆.第二年,当他把这种杂交长茎豌豆再种下时,得到的却既有长茎豌豆,又有短茎豌豆.试验的具体数据如下:你能从这些数据中发现什么规律吗?
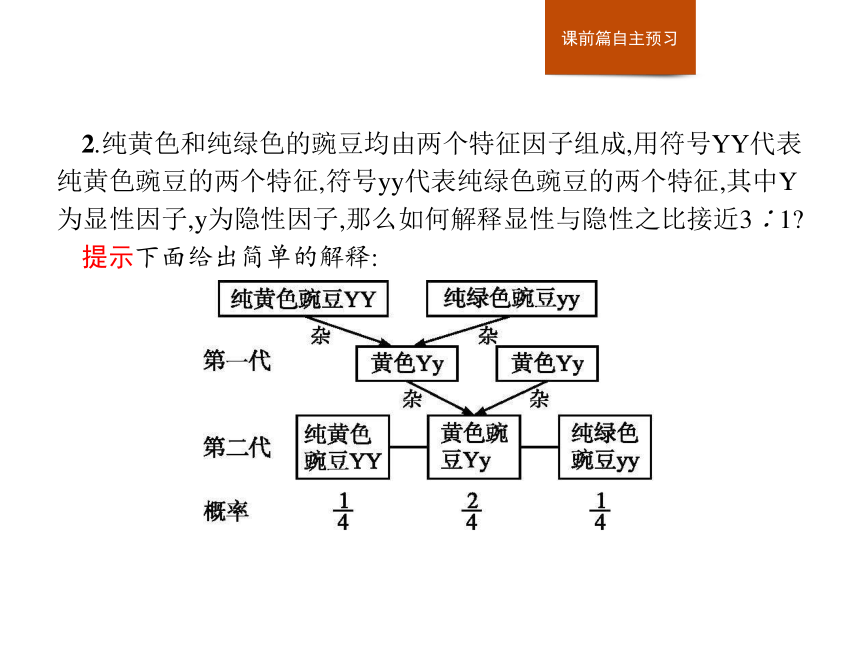
提示孟德尔的豌豆试验表明,外表完全相同的杂交豌豆会长出不同的后代,并且每次试验的显性与隐性之比都接近3∶1.2.纯黄色和纯绿色的豌豆均由两个特征因子组成,用符号YY代表纯黄色豌豆的两个特征,符号yy代表纯绿色豌豆的两个特征,其中Y为显性因子,y为隐性因子,那么如何解释显性与隐性之比接近3∶1?
提示下面给出简单的解释:探究一探究二探究三正确理解概率的意义
例1 下列说法正确的是( )
A.由《生物学》知道生男生女的概率约为0.5,一对夫妇先后生两个小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
分析概率只是说明事件发生的可能性大小.当堂检测探究一探究二探究三解析:一对夫妇生两个小孩可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确;D正确.
答案:D当堂检测探究一探究二探究三反思感悟从三个方面理解概率的意义
(1)概率是随机事件发生可能性大小的度量,是随机事件A的本质属性,随机事件A发生的概率是大量重复试验中事件A发生的频率的近似值.
(2)由概率的定义我们可以知道随机事件A在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
(3)正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.当堂检测探究一探究二探究三变式训练1某地气象局预报说,明天本地降水概率为80%,你认为下面哪一个解释能表明气象局的观点?
A.明天本地有80%的时间下雨,20%的时间不下雨
B.明天本地有80%的区域下雨,20%的区域不下雨
C.明天本地下雨的机会是80%
D.气象局并没有对明天是否下雨作出有意义的预报
解析:根据概率的意义,“明天降水的概率为80%”的正确解释是“明天下雨的机会是80%”.
答案:C当堂检测探究一探究二探究三例2如图,有两个可以自由转动的均匀转盘A,B.转盘A被平均分成3等份,分别标上1,2,3三个数字;转盘B被平均分成4等份,分别标上3,4,5,6四个数字.有人为甲、乙两人设计了一个游戏规则:自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则乙获胜.你认为这样的游戏规则公平吗?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏公平?
游戏的公平性 当堂检测探究一探究二探究三 分析要判断游戏规则是否公平,只要看甲、乙两人获胜的概率是否相等,即只要看甲、乙两人获胜的概率是否都等于 即可.若游戏规则不公平,修改游戏规则也要按照这个标准来修改.当堂检测探究一探究二探究三 互动探究 本例中,若将游戏规则改为:自由转动转盘A和B,转盘停止后,两个指针指向的两个数字相乘,如果是偶数,那么甲获胜,否则乙获胜,游戏规则公平吗?当堂检测探究一探究二探究三反思感悟游戏公平性的标准及判断方法
(1)游戏规则是否公平,要看对游戏的双方来说获胜的可能性或概率是否相同.若相同,则规则公平,否则就是不公平的.
(2)具体判断时,可以求出按所给规则双方的获胜概率,再进行比较.当堂检测探究一探究二探究三极大似然法的应用
例3在使用计算机输入法时,英语中某些字母出现的概率远远高于另一些字母.进一步深入研究之后,人们发现各字母被使用的频率相当稳定,下面就是英文字母使用频率的一份统计表:
请你用概率的知识解释一下计算机键盘设计成现在这个形状的原因.由此,请对汉字的重码问题的设计谈谈你的体会.当堂检测探究一探究二探究三解:从统计表可以看出,空格键被使用的频率最高,鉴于此,人们在设计键盘时,空格键不仅最大,而且放在了最方便使用的位置.同理,其他字母键的排列也是按照其被使用的频率的大小来放置的.
近年来,人们对汉字的统计研究有了很大的发展.关于汉字的使用频率已有初步的统计资料,对汉语常用词汇也进行了一些统计研究,这些信息对汉字输入方案等研究有很大的帮助,使用过汉字拼音输入法的同学们可能有体会,例如,若输入拼音“shu”,则提示有以下汉字供选择:“1.数,2.书,3.树,4.属,5.署……”.这个显示顺序基本上就是按照拼音为“shu”的汉字出现频率从大到小来排列的.(答案不唯一,合理即可)当堂检测探究一探究二探究三反思感悟 1.任何事件的概率是0到1之间的一个数,它度量该事件发生的可能性.小概率(接近0)事件很少发生,而大概率(接近1)事件则经常发生.
2.在一次试验中,概率大的事件比概率小的事件出现的可能性大,这正是我们能够利用极大似然法来进行科学决策的理论依据.当堂检测探究一探究二探究三变式训练2投掷一枚硬币,连续出现10次正面朝上,试就下面情况进行分析:当堂检测探究一探究二探究三当堂检测1.设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数可能为( )
A.160 B.7 840 C.7 998 D.7 800
解析:次品率为2%,故次品约8 000×2%=160(件),故合格品的件数可能为7 840件.
答案:B探究一探究二探究三当堂检测2.下列说法正确的是( )
A.某事件发生的概率为P(A)=1.1
B.不可能事件的概率为0,必然事件的概率为1
C.小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件
D.某事件发生的概率是随着试验次数的变化而变化的
解析:∵事件发生的概率0≤P(A)≤1,∴A错;小概率事件是指这个事件发生的可能性很小,几乎不发生.大概率事件发生的可能性较大,但并不是一定发生,∴C错;某事件发生的概率为一个常数,不随试验次数的变化而变化,∴D错;故B正确.
答案:B探究一探究二探究三当堂检测3.抛掷一枚质地均匀的硬币10次,其中前9次有4次正面向上,则第10次( )
A.一定是正面向上
B.一定是反面向上
解析:因为硬币是均匀的,所以每一次掷硬币,正面向上的概率都是 .
答案:D探究一探究二探究三当堂检测4.给出下列四个命题:
①设有一批产品,其次品率为0.05,则从中任取200件,必有10件是次品;
②做100次抛质地均匀的硬币的试验,结果51次出现正面朝上,因此,出现正面朝上的概率是
③随机事件发生的频率就是这个随机事件发生的概率;
④抛掷质地均匀的骰子100次,得点数是1的结果18次,则出现1点的频率是
其中真命题有 .?(填序号)
解析:①错,次品率是大量产品的估计值,并不是针对200件产品来说的.②③混淆了频率与概率的区别.④正确.
答案:④探究一探究二探究三当堂检测
1.有人说,既然抛掷一枚质地均匀的硬币出现正面朝上的概率为0.5,那么连续两次抛掷一枚质地均匀的硬币,一定是一次正面朝上,一次反面朝上,你认为这种说法正确吗?
提示这种说法是错误的,抛掷一枚质地均匀的硬币出现正面朝上的概率为0.5,它是大量试验得出的一种规律性结果,对具体的几次试验来讲不一定能体现出这种规律性,在连续抛掷一枚质地均匀的硬币两次的试验中,可能两次均正面朝上,也可能两次均反面朝上,也可能一次正面朝上,一次反面朝上.2.若某种彩票准备发行1 000万张,其中有1万张可以中奖,则买一张这种彩票的中奖概率是多少?买1 000张的话是否一定会中奖?3.填空:随机事件在一次试验中发生与否是随机的,但随机性中含有规律性,认识了这种随机性中的规律性,就能比较准确地预测随机事件发生的可能性.
4.做一做1:掷一枚均匀的硬币,正面向上的概率是 ,那么在掷一百次试验中,正面向上的次数是( )
A.50 B.大于50 C.小于50 D.大约50
答案:D二、游戏的公平性
1.甲、乙两人做游戏,从装有3个白球1个黑球的袋子中任取1球,如果是白球,甲胜;否则,乙胜.试问这个游戏对两个人来说公平吗?谁获胜的机会大一些?
提示不公平.甲获胜的机会大一些.
2.在乒乓球比赛前,要决定由谁先发球.裁判员拿出一个抽签器(一个像大硬币似的均匀塑料圆板,一面是红圈,一面是绿圈),然后随意指定一名运动员,要他猜上抛的抽签器落到球台上时,是红圈那面朝上还是绿圈那面朝上.如果他猜对了,就由他先发球,否则,由另一方先发球.你认为公平吗?为什么?
提示公平.因为当抽签器上抛后,红圈朝上与绿圈朝上的概率都是0.5,因此任何一名运动员猜中的概率都是0.5,也就是每个运动员取得发球权的概率均为0.5,所以这个规则是公平的.3.填空:在设计某种游戏规则时,一定要考虑这种规则对每个人都是公平的这一重要原则.
三、决策中的概率思想
1.如果连续10次掷一枚骰子,结果都是出现1点,你认为这枚骰子的质地均匀吗?为什么?
提示可以推测这枚骰子的质地不均匀,并且很有可能是标有6点的那面比较重,使得出现1点的概率最大,才会连续10次都出现1点.2.填空:如果我们面临的是从多个可选答案中挑选正确答案的决策任务,那么“使得样本出现的可能性最大”可以作为决策的准则,这种判断问题的方法称为极大似然法.极大似然法是统计中重要的统计思想方法之一.
3.做一做2:如果掷一枚硬币100次,结果只有2次正面向上,如果只考虑硬币是否均匀,我们的判断是 .?
答案:硬币是不均匀的四、天气预报的概率解释
1.“昨天没有下雨,而天气预报说昨天降水的概率为90%.这说明预报是错误的”这种说法科学吗?
提示不科学.
2.填空:天气预报的“降水”是一个随机事件,“概率为90%”指明了“降水”这个随机事件发生的概率为90%.在一次试验中,概率为90%的事件也可能不出现.因此,“昨天没有下雨”并不能说明“昨天的降水概率为90%”的天气预报是错误的.五、试验与发现、遗传机理中的统计规律
1.奥地利遗传学家孟德尔1856年开始用豌豆作试验,他把黄色和绿色的豌豆杂交,第一年收获的豌豆都是黄色的.第二年,当他把第一年收获的黄色豌豆再种下时,收获的豌豆既有黄色的又有绿色的.同样他把圆形和皱皮豌豆杂交,第一年收获的豌豆都是圆形的.第二年,当他把第一年收获的圆形豌豆再种下时,收获的却既有圆形豌豆,又有皱皮豌豆.类似地,他把长茎的豌豆与短茎的豌豆杂交,第一年长出来的都是长茎的豌豆.第二年,当他把这种杂交长茎豌豆再种下时,得到的却既有长茎豌豆,又有短茎豌豆.试验的具体数据如下:你能从这些数据中发现什么规律吗?
提示孟德尔的豌豆试验表明,外表完全相同的杂交豌豆会长出不同的后代,并且每次试验的显性与隐性之比都接近3∶1.2.纯黄色和纯绿色的豌豆均由两个特征因子组成,用符号YY代表纯黄色豌豆的两个特征,符号yy代表纯绿色豌豆的两个特征,其中Y为显性因子,y为隐性因子,那么如何解释显性与隐性之比接近3∶1?
提示下面给出简单的解释:探究一探究二探究三正确理解概率的意义
例1 下列说法正确的是( )
A.由《生物学》知道生男生女的概率约为0.5,一对夫妇先后生两个小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
分析概率只是说明事件发生的可能性大小.当堂检测探究一探究二探究三解析:一对夫妇生两个小孩可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确;D正确.
答案:D当堂检测探究一探究二探究三反思感悟从三个方面理解概率的意义
(1)概率是随机事件发生可能性大小的度量,是随机事件A的本质属性,随机事件A发生的概率是大量重复试验中事件A发生的频率的近似值.
(2)由概率的定义我们可以知道随机事件A在一次试验中发生与否是随机的,但随机中含有规律性,而概率就是其规律性在数量上的反映.
(3)正确理解概率的意义,要清楚概率与频率的区别与联系.对具体的问题要从全局和整体上去看待,而不是局限于某一次试验或某一个具体的事件.当堂检测探究一探究二探究三变式训练1某地气象局预报说,明天本地降水概率为80%,你认为下面哪一个解释能表明气象局的观点?
A.明天本地有80%的时间下雨,20%的时间不下雨
B.明天本地有80%的区域下雨,20%的区域不下雨
C.明天本地下雨的机会是80%
D.气象局并没有对明天是否下雨作出有意义的预报
解析:根据概率的意义,“明天降水的概率为80%”的正确解释是“明天下雨的机会是80%”.
答案:C当堂检测探究一探究二探究三例2如图,有两个可以自由转动的均匀转盘A,B.转盘A被平均分成3等份,分别标上1,2,3三个数字;转盘B被平均分成4等份,分别标上3,4,5,6四个数字.有人为甲、乙两人设计了一个游戏规则:自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜,否则乙获胜.你认为这样的游戏规则公平吗?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏公平?
游戏的公平性 当堂检测探究一探究二探究三 分析要判断游戏规则是否公平,只要看甲、乙两人获胜的概率是否相等,即只要看甲、乙两人获胜的概率是否都等于 即可.若游戏规则不公平,修改游戏规则也要按照这个标准来修改.当堂检测探究一探究二探究三 互动探究 本例中,若将游戏规则改为:自由转动转盘A和B,转盘停止后,两个指针指向的两个数字相乘,如果是偶数,那么甲获胜,否则乙获胜,游戏规则公平吗?当堂检测探究一探究二探究三反思感悟游戏公平性的标准及判断方法
(1)游戏规则是否公平,要看对游戏的双方来说获胜的可能性或概率是否相同.若相同,则规则公平,否则就是不公平的.
(2)具体判断时,可以求出按所给规则双方的获胜概率,再进行比较.当堂检测探究一探究二探究三极大似然法的应用
例3在使用计算机输入法时,英语中某些字母出现的概率远远高于另一些字母.进一步深入研究之后,人们发现各字母被使用的频率相当稳定,下面就是英文字母使用频率的一份统计表:
请你用概率的知识解释一下计算机键盘设计成现在这个形状的原因.由此,请对汉字的重码问题的设计谈谈你的体会.当堂检测探究一探究二探究三解:从统计表可以看出,空格键被使用的频率最高,鉴于此,人们在设计键盘时,空格键不仅最大,而且放在了最方便使用的位置.同理,其他字母键的排列也是按照其被使用的频率的大小来放置的.
近年来,人们对汉字的统计研究有了很大的发展.关于汉字的使用频率已有初步的统计资料,对汉语常用词汇也进行了一些统计研究,这些信息对汉字输入方案等研究有很大的帮助,使用过汉字拼音输入法的同学们可能有体会,例如,若输入拼音“shu”,则提示有以下汉字供选择:“1.数,2.书,3.树,4.属,5.署……”.这个显示顺序基本上就是按照拼音为“shu”的汉字出现频率从大到小来排列的.(答案不唯一,合理即可)当堂检测探究一探究二探究三反思感悟 1.任何事件的概率是0到1之间的一个数,它度量该事件发生的可能性.小概率(接近0)事件很少发生,而大概率(接近1)事件则经常发生.
2.在一次试验中,概率大的事件比概率小的事件出现的可能性大,这正是我们能够利用极大似然法来进行科学决策的理论依据.当堂检测探究一探究二探究三变式训练2投掷一枚硬币,连续出现10次正面朝上,试就下面情况进行分析:当堂检测探究一探究二探究三当堂检测1.设某厂产品的次品率为2%,估算该厂8 000件产品中合格品的件数可能为( )
A.160 B.7 840 C.7 998 D.7 800
解析:次品率为2%,故次品约8 000×2%=160(件),故合格品的件数可能为7 840件.
答案:B探究一探究二探究三当堂检测2.下列说法正确的是( )
A.某事件发生的概率为P(A)=1.1
B.不可能事件的概率为0,必然事件的概率为1
C.小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件
D.某事件发生的概率是随着试验次数的变化而变化的
解析:∵事件发生的概率0≤P(A)≤1,∴A错;小概率事件是指这个事件发生的可能性很小,几乎不发生.大概率事件发生的可能性较大,但并不是一定发生,∴C错;某事件发生的概率为一个常数,不随试验次数的变化而变化,∴D错;故B正确.
答案:B探究一探究二探究三当堂检测3.抛掷一枚质地均匀的硬币10次,其中前9次有4次正面向上,则第10次( )
A.一定是正面向上
B.一定是反面向上
解析:因为硬币是均匀的,所以每一次掷硬币,正面向上的概率都是 .
答案:D探究一探究二探究三当堂检测4.给出下列四个命题:
①设有一批产品,其次品率为0.05,则从中任取200件,必有10件是次品;
②做100次抛质地均匀的硬币的试验,结果51次出现正面朝上,因此,出现正面朝上的概率是
③随机事件发生的频率就是这个随机事件发生的概率;
④抛掷质地均匀的骰子100次,得点数是1的结果18次,则出现1点的频率是
其中真命题有 .?(填序号)
解析:①错,次品率是大量产品的估计值,并不是针对200件产品来说的.②③混淆了频率与概率的区别.④正确.
答案:④探究一探究二探究三当堂检测
