高中数学人教A版必修三课件 3.2.2古典概型 (整数值)随机数的产生 :26张PPT
文档属性
| 名称 | 高中数学人教A版必修三课件 3.2.2古典概型 (整数值)随机数的产生 :26张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览








文档简介
课件26张PPT。3.2.2 (整数值)随机数(random numbers)的产生一、随机数的产生
通过做大量重复的试验来计算事件发生的频率,再由频率的稳定值估计概率,是十分费时费力的.有没有其他方法可以代替试验呢?我们设想通过用计算机模拟试验来解决这些矛盾.
1.我们要产生1~25之间的随机整数,可以把25个大小形状相同的小球分别标上1,2,3,…,24,25,放入一个袋中,把它们充分搅拌,然后从中摸出一个,这个球上的数就称为随机数,这种产生随机数的方法是什么?
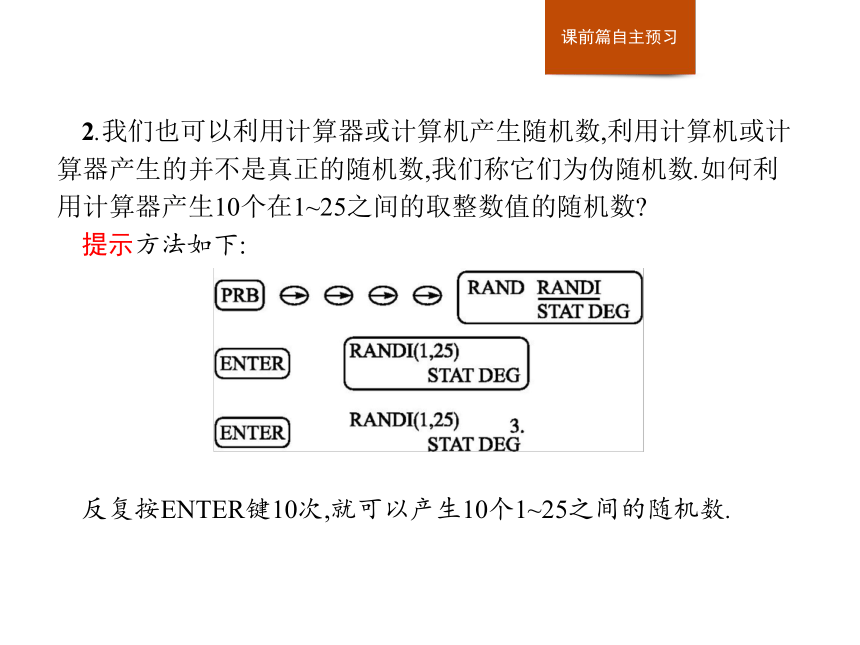
提示是简单随机抽样中的抽签法.2.我们也可以利用计算器或计算机产生随机数,利用计算机或计算器产生的并不是真正的随机数,我们称它们为伪随机数.如何利用计算器产生10个在1~25之间的取整数值的随机数?
提示方法如下:
反复按ENTER键10次,就可以产生10个1~25之间的随机数.3.以掷均匀硬币为例,如何利用计算机中的Excel软件不断地产生0,1这两个随机数?
提示用Excel演示:
(1)选定A1格,键入“=RANDBETWEEN(0,1)”,按Enter键,则在此格中的数是随机产生的0或1;(2)选定A1格,点击复制,然后选定要产生随机数的格,比如A2至A100,点击粘贴,则在A2至A100的数均为随机产生的0或1,这样我们就很快就得到了100个随机产生的0,1,相当于做了100次随机试验.
4.如果需要统计抛掷一枚质地均匀的骰子30次时各面朝上的频数,但是没有骰子,你有什么办法得到试验的结果?
提示由计算器或计算机产生30个1~6之间的随机数.5.一般地,如果一个古典概型的基本事件总数为n,在没有试验条件的情况下,你有什么办法进行m次试验,并得到相应的试验结果?
提示将n个基本事件编号为1,2,…,n,由计算器或计算机产生m个1~n之间的随机数.6.做一做1:判断题
(1)随机模拟方法只适用于试验结果有限的试验. ( )
(2)随机数是用计算机或计算器随便按键产生的数. ( )
(3)用计算器或计算机产生的随机数是伪随机数. ( )
(4)不能用伪随机数估计概率. ( )
答案:(1)√ (2)× (3)√ (4)×7.做一做2:用掷质地均匀的硬币的方法可产生 个随机数,掷质地均匀的骰子可产生 个随机数.?
解析:掷硬币,用正面表示一个数,反面表示一个数,则可产生两个随机数,类似地,掷骰子可产生六个随机数.
答案:2 6二、随机模拟方法
1.对于古典概型,我们可以将随机试验中所有基本事件编号,利用计算器或计算机产生随机数,从而获得试验结果.这种用计算器或计算机模拟试验的方法,称为随机模拟方法或蒙特卡罗方法.你认为这种方法的最大优点是什么?
提示不需要对试验进行具体操作,可以广泛应用到各个领域.2.如果用随机模拟方法抛掷一枚质地均匀的硬币100次,那么如何用计算机统计出这100次试验中“出现正面朝上”的频数和频率?
提示利用计算机统计频数和频率,用Excel演示如下:
选定C1格,键入频数函数“=FREQUENCY(A1∶A100,0.5)”,
按Enter键,则此格中的数是统计A1至A100中,比0.5小的数的个数,即0出现的频数,也就是反面朝上的频数.选定D1格,键入“=1-C1/100”,按Enter键,在此格中的数是这100次试验中出现1的频率,即正面朝上的频率.3.做一做2:通过模拟试验,产生了20组随机数:
6830 3013 7055 7430 7740 4422 7884
2604 3346 0952 6807 9706 5774 5725
6576 5929 9768 6071 9138 6754
如果恰有三个数在1,2,3,4,5,6中,表示恰有三次击中目标,则四次射击中恰有三次击中目标的概率约为 .?
解析:表示三次击中目标分别是3013,2604,5725,6576,6754,共5组数,而随机数总共20组,所以所求的概率约为 =25%.
答案:25%探究一探究二探究三思维辨析例1 某校高一全年级20个班共1 200人,期中考试时如何把学生分配到40个考场去?
分析用计算机产生的随机数给1 200名学生编号,把学生按分到的随机数从小到大排列.
解:(1)按班级、学号顺序把学生档案输入计算机;
(2)用随机函数RANDBETWEEN(1,1 200)按顺序给每个学生一个随机数(每人的都不同);
(3)使用计算机排序功能按随机数从小到大排列,即可得到考试号从1到1 200人的考试序号.(注:1号应为0001,2号应为0002,用0补足位数.前面再加上有关信息号码即可)随机数的产生 当堂检测探究一探究二探究三思维辨析反思感悟1.产生随机数的方法有抽签法、利用计算机或计算器产生随机数的随机模拟方法等.抽签法产生的随机数能保证机会均等,而计算器或计算机产生的随机数是伪随机数,不能保证等可能性,但是后者较前者速度快,操作简单,省时省力.
2.用产生随机数的方法抽取样本要注意以下两点:(1)进行正确的编号,并且编号要连续;(2)正确把握抽取的范围和容量.当堂检测探究一探究二探究三思维辨析变式训练1一体育代表队共有21名水平相当的运动员,现从中抽取11人参加某场比赛,其中运动员甲必须参加.写出利用随机数抽取的过程.
解:(1)把除甲之外的20名运动员编号,号码为1,2,3,…,19,20;
(2)用计算器的随机函数RANDI(1,20)或计算机的随机函数RANDBETWEEN(1,20)产生10个1~20之间的整数值随机数,如果有重复,就重新产生一个;
(3)以上号码对应的10名运动员与甲运动员就是要抽取的对象.当堂检测探究一探究二探究三思维辨析例2 盒中有除颜色外其他均相同的5个白球和2个黑球,用随机模拟法求下列事件的概率:
(1)任取一球,得到白球;
(2)任取三球,都是白球.
分析将这7个球编号,产生1到7之间的整数值的随机数,(1)一个随机数看成一组即代表一次试验;(2)每三个随机数看成一组即代表一次试验.统计组数和事件发生的次数即可.估计古典概型的概率 当堂检测探究一探究二探究三思维辨析解:用1,2,3,4,5表示白球,6,7表示黑球.
(1)步骤:
①利用计算器或计算机产生1到7之间的整数随机数,每一个数一组,统计组数为n;
②统计这n组数中小于6的组数m;
③则任取一球,得到白球的概率近似为 .
(2)步骤:
①利用计算器或计算机产生1到7之间的整数随机数,每三个数一组(每组中数不重复),统计组数为n';
②统计这n组数中,每组三个数字均小于6的组数m';
③则任取三球,都是白球的概率近似为 .当堂检测探究一探究二探究三思维辨析反思感悟用整数随机模拟试验估计古典概型的概率时,首先要确定整数随机数的范围和用哪些数代表不同的试验结果.可以从以下几个方面考虑:
(1)试验的基本事件是等可能的时,基本事件总数就是产生随机数的范围,每组随机数字代表一个基本事件;
(2)按比例确定表示各个结果的数字个数及总个数;
(3)产生的整数随机数的组数n越大,估计的概率准确性越高;
(4)这种用模拟试验来求概率的方法所得结果是不精确的,且每次模拟试验最终得到的概率值不一定是相同的. 当堂检测探究一探究二探究三思维辨析变式训练2从甲、乙、丙、丁4人中,任选3人参加志愿者活动,请用随机模拟的方法估计甲被选中的概率.
解:用1,2,3,4分别表示甲、乙、丙、丁四人.
利用计算器或计算机产生1到4之间的随机数,每三个一组,每组中数不重复,得到n组数,统计这n组数中含有1的组数m,则估计甲被选中的概率为 .当堂检测探究一探究二探究三思维辨析n次重复试验恰好发生k次的概率
例3一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
分析试验的结果有两个,但是两个结果“猜对”“猜错”不是等可能的→用计算机或计算器做模拟试验,模拟每次猜对的概率是25%.当堂检测探究一探究二探究三思维辨析解:我们通过设计模拟试验的方法来解决问题.利用计算机或计算器可以产生0到3之间取整数值的随机数.我们用0表示猜的选项正确,1,2,3表示猜的选项错误,这样可以体现猜对的概率是25%.因为共猜6道题,所以每6个随机数作为一组.例如,产生25组随机数.
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相当于做了25次试验,在每组数中,如果恰有3个或3个以上的数是0,则表示至少答对3道题,它们分别是001003,030032,210010,112000,共有4组数,由此可得该同学6道选择题至少答对3道的概率近似为 =0.16.当堂检测探究一探究二探究三思维辨析反思感悟如果事件A在每次试验中发生的概率都相等,那么可以用随机模拟方法估计n次重复试验中事件A恰好发生k次的概率,其步骤是:
(1)按事件A的概率确定表示各个结果的数字个数及总个数;
(2)利用计算机或计算器产生整数随机数,然后n个整数随机数作为一组分组.每组第1个数表示第1次试验,第2个数表示第2次试验,第3个数表示第3次试验,…,第n个数表示第n次试验.n个随机数作为一组共组成N组数;
(3)统计这N组数中恰有k个数字在表示试验发生的数组中的组数m.
则n次重复试验中事件A恰好发生k次的概率近似为 .当堂检测探究一探究二探究三思维辨析变式训练3一个袋中有7个大小、形状相同的小球,6个白球,1个红球,现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取,试设计一个模拟试验,计算恰好第三次摸到红球的概率.
解用1,2,3,4,5,6表示白球,7表示红球,利用计算器或计算机产生1到7之间(包括1和7)取整数值的随机数.因为要求恰好第三次摸到红球的概率,所以每三个随机数作为一组.如下,产生20组随机数:
666 743 671 464 571
561 156 567 732 375
716 116 614 445 117
573 552 274 114 662
就相当于做了20次试验,在这些数组中,前两个数字不是7,第三个数字恰好是7就表示第一次、第二次摸到的是白球,第三次摸到的是红球,它们分别是567和117,共两组,因此恰好第三次摸到红球的概率约为当堂检测探究一探究二探究三思维辨析不理解随机数的意义,弄错随机数的范围而致误
典例 同时抛掷两枚质地均匀的骰子,用随机模拟法求所得点数之和是偶数的概率.
错解(1)用计算器产生1~10之间取整数值的随机数.
(2)统计所产生的随机数总个数N.
(3)把所产生的随机数两两分组,再相加,统计和是偶数的个数N1.
(4) 即是点数之和是偶数的概率近似值.
以上错解中都有哪些错误?出错的原因是什么?你如何订正?你如何防范?
错因分析骰子的点数为1~6之间的整数,故随机数的范围应设为1~6,并且每个数代表骰子出现的点数.错解中,没有理解随机数产生范围的含义,错误地把随机数的范围当作1~10,因此所求结果是错的.当堂检测探究一探究二探究三思维辨析正解抛掷两枚骰子,可以看作一枚骰子抛掷两次,用两个随机数字作为一组即可.
(1)抛掷一次只能出现6个等可能基本事件,所以用1~6之间的数字进行标注.
(2)用计算器或计算机产生1~6之间的取整数值的随机数,并用两个随机数值作为一组.
(3)统计随机数总组数N及两个随机数之和为偶数的组数N1.则所得点数之和为偶数的频率值就是 .
当模拟次数足够大时,可用频率近似作概率值,即所求概率约为 .
防范措施1.明确随机数的取值范围.
2.该种模拟用于试验结果是有限个的情况,每次模拟得到的近似概率不一定相同.当堂检测1.用计算机随机模拟方法估计概率时,其准确程度取决于( )
A.产生的随机数的大小 B.产生的随机数的个数
C.随机数对应的结果 D.产生随机数的方法
解析:随机数容量越大,概率越接近实际数.
答案:B探究一探究二探究三思维辨析当堂检测2.用计算器或计算机随机模拟掷质地均匀的骰子的试验,估计出现2点的概率,下列步骤中,不正确的是( )
A.用计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生6个不同的1到6之间的取整数值的随机数x,如果x=2,我们认为出现2点
B.我们通常用计数器n记录做了多少次掷骰子试验,用计数器m记录其中有多少次出现2点,掷n=0,m=0
C.出现2点,则m的值加1,即m=m+1;否则m的值保持不变
D.程序结束,出现2点的频率 作为概率的近似值
解析:计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生的是1到7之间的整数,包括7,共7个整数,而骰子只有6个面,A不正确,故选A.
答案:A探究一探究二探究三思维辨析当堂检测3.抛掷一枚质地均匀的骰子两次,用随机模拟方法估计朝上面的点数和为8的概率,共进行了两次试验,第一次产生了60组随机数,第二次产生了200组随机数,那么这两次估计的结果相比较,第 次准确.?
解析:用随机模拟方法估计概率时,产生的随机数组数越多,估计的结果越准确,所以第二次比第一次准确.
答案:二探究一探究二探究三思维辨析当堂检测
通过做大量重复的试验来计算事件发生的频率,再由频率的稳定值估计概率,是十分费时费力的.有没有其他方法可以代替试验呢?我们设想通过用计算机模拟试验来解决这些矛盾.
1.我们要产生1~25之间的随机整数,可以把25个大小形状相同的小球分别标上1,2,3,…,24,25,放入一个袋中,把它们充分搅拌,然后从中摸出一个,这个球上的数就称为随机数,这种产生随机数的方法是什么?
提示是简单随机抽样中的抽签法.2.我们也可以利用计算器或计算机产生随机数,利用计算机或计算器产生的并不是真正的随机数,我们称它们为伪随机数.如何利用计算器产生10个在1~25之间的取整数值的随机数?
提示方法如下:
反复按ENTER键10次,就可以产生10个1~25之间的随机数.3.以掷均匀硬币为例,如何利用计算机中的Excel软件不断地产生0,1这两个随机数?
提示用Excel演示:
(1)选定A1格,键入“=RANDBETWEEN(0,1)”,按Enter键,则在此格中的数是随机产生的0或1;(2)选定A1格,点击复制,然后选定要产生随机数的格,比如A2至A100,点击粘贴,则在A2至A100的数均为随机产生的0或1,这样我们就很快就得到了100个随机产生的0,1,相当于做了100次随机试验.
4.如果需要统计抛掷一枚质地均匀的骰子30次时各面朝上的频数,但是没有骰子,你有什么办法得到试验的结果?
提示由计算器或计算机产生30个1~6之间的随机数.5.一般地,如果一个古典概型的基本事件总数为n,在没有试验条件的情况下,你有什么办法进行m次试验,并得到相应的试验结果?
提示将n个基本事件编号为1,2,…,n,由计算器或计算机产生m个1~n之间的随机数.6.做一做1:判断题
(1)随机模拟方法只适用于试验结果有限的试验. ( )
(2)随机数是用计算机或计算器随便按键产生的数. ( )
(3)用计算器或计算机产生的随机数是伪随机数. ( )
(4)不能用伪随机数估计概率. ( )
答案:(1)√ (2)× (3)√ (4)×7.做一做2:用掷质地均匀的硬币的方法可产生 个随机数,掷质地均匀的骰子可产生 个随机数.?
解析:掷硬币,用正面表示一个数,反面表示一个数,则可产生两个随机数,类似地,掷骰子可产生六个随机数.
答案:2 6二、随机模拟方法
1.对于古典概型,我们可以将随机试验中所有基本事件编号,利用计算器或计算机产生随机数,从而获得试验结果.这种用计算器或计算机模拟试验的方法,称为随机模拟方法或蒙特卡罗方法.你认为这种方法的最大优点是什么?
提示不需要对试验进行具体操作,可以广泛应用到各个领域.2.如果用随机模拟方法抛掷一枚质地均匀的硬币100次,那么如何用计算机统计出这100次试验中“出现正面朝上”的频数和频率?
提示利用计算机统计频数和频率,用Excel演示如下:
选定C1格,键入频数函数“=FREQUENCY(A1∶A100,0.5)”,
按Enter键,则此格中的数是统计A1至A100中,比0.5小的数的个数,即0出现的频数,也就是反面朝上的频数.选定D1格,键入“=1-C1/100”,按Enter键,在此格中的数是这100次试验中出现1的频率,即正面朝上的频率.3.做一做2:通过模拟试验,产生了20组随机数:
6830 3013 7055 7430 7740 4422 7884
2604 3346 0952 6807 9706 5774 5725
6576 5929 9768 6071 9138 6754
如果恰有三个数在1,2,3,4,5,6中,表示恰有三次击中目标,则四次射击中恰有三次击中目标的概率约为 .?
解析:表示三次击中目标分别是3013,2604,5725,6576,6754,共5组数,而随机数总共20组,所以所求的概率约为 =25%.
答案:25%探究一探究二探究三思维辨析例1 某校高一全年级20个班共1 200人,期中考试时如何把学生分配到40个考场去?
分析用计算机产生的随机数给1 200名学生编号,把学生按分到的随机数从小到大排列.
解:(1)按班级、学号顺序把学生档案输入计算机;
(2)用随机函数RANDBETWEEN(1,1 200)按顺序给每个学生一个随机数(每人的都不同);
(3)使用计算机排序功能按随机数从小到大排列,即可得到考试号从1到1 200人的考试序号.(注:1号应为0001,2号应为0002,用0补足位数.前面再加上有关信息号码即可)随机数的产生 当堂检测探究一探究二探究三思维辨析反思感悟1.产生随机数的方法有抽签法、利用计算机或计算器产生随机数的随机模拟方法等.抽签法产生的随机数能保证机会均等,而计算器或计算机产生的随机数是伪随机数,不能保证等可能性,但是后者较前者速度快,操作简单,省时省力.
2.用产生随机数的方法抽取样本要注意以下两点:(1)进行正确的编号,并且编号要连续;(2)正确把握抽取的范围和容量.当堂检测探究一探究二探究三思维辨析变式训练1一体育代表队共有21名水平相当的运动员,现从中抽取11人参加某场比赛,其中运动员甲必须参加.写出利用随机数抽取的过程.
解:(1)把除甲之外的20名运动员编号,号码为1,2,3,…,19,20;
(2)用计算器的随机函数RANDI(1,20)或计算机的随机函数RANDBETWEEN(1,20)产生10个1~20之间的整数值随机数,如果有重复,就重新产生一个;
(3)以上号码对应的10名运动员与甲运动员就是要抽取的对象.当堂检测探究一探究二探究三思维辨析例2 盒中有除颜色外其他均相同的5个白球和2个黑球,用随机模拟法求下列事件的概率:
(1)任取一球,得到白球;
(2)任取三球,都是白球.
分析将这7个球编号,产生1到7之间的整数值的随机数,(1)一个随机数看成一组即代表一次试验;(2)每三个随机数看成一组即代表一次试验.统计组数和事件发生的次数即可.估计古典概型的概率 当堂检测探究一探究二探究三思维辨析解:用1,2,3,4,5表示白球,6,7表示黑球.
(1)步骤:
①利用计算器或计算机产生1到7之间的整数随机数,每一个数一组,统计组数为n;
②统计这n组数中小于6的组数m;
③则任取一球,得到白球的概率近似为 .
(2)步骤:
①利用计算器或计算机产生1到7之间的整数随机数,每三个数一组(每组中数不重复),统计组数为n';
②统计这n组数中,每组三个数字均小于6的组数m';
③则任取三球,都是白球的概率近似为 .当堂检测探究一探究二探究三思维辨析反思感悟用整数随机模拟试验估计古典概型的概率时,首先要确定整数随机数的范围和用哪些数代表不同的试验结果.可以从以下几个方面考虑:
(1)试验的基本事件是等可能的时,基本事件总数就是产生随机数的范围,每组随机数字代表一个基本事件;
(2)按比例确定表示各个结果的数字个数及总个数;
(3)产生的整数随机数的组数n越大,估计的概率准确性越高;
(4)这种用模拟试验来求概率的方法所得结果是不精确的,且每次模拟试验最终得到的概率值不一定是相同的. 当堂检测探究一探究二探究三思维辨析变式训练2从甲、乙、丙、丁4人中,任选3人参加志愿者活动,请用随机模拟的方法估计甲被选中的概率.
解:用1,2,3,4分别表示甲、乙、丙、丁四人.
利用计算器或计算机产生1到4之间的随机数,每三个一组,每组中数不重复,得到n组数,统计这n组数中含有1的组数m,则估计甲被选中的概率为 .当堂检测探究一探究二探究三思维辨析n次重复试验恰好发生k次的概率
例3一份测试题包括6道选择题,每题只有一个选项是正确的.如果一个学生对每一道题都随机猜一个答案,用随机模拟方法估计该学生至少答对3道题的概率.
分析试验的结果有两个,但是两个结果“猜对”“猜错”不是等可能的→用计算机或计算器做模拟试验,模拟每次猜对的概率是25%.当堂检测探究一探究二探究三思维辨析解:我们通过设计模拟试验的方法来解决问题.利用计算机或计算器可以产生0到3之间取整数值的随机数.我们用0表示猜的选项正确,1,2,3表示猜的选项错误,这样可以体现猜对的概率是25%.因为共猜6道题,所以每6个随机数作为一组.例如,产生25组随机数.
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相当于做了25次试验,在每组数中,如果恰有3个或3个以上的数是0,则表示至少答对3道题,它们分别是001003,030032,210010,112000,共有4组数,由此可得该同学6道选择题至少答对3道的概率近似为 =0.16.当堂检测探究一探究二探究三思维辨析反思感悟如果事件A在每次试验中发生的概率都相等,那么可以用随机模拟方法估计n次重复试验中事件A恰好发生k次的概率,其步骤是:
(1)按事件A的概率确定表示各个结果的数字个数及总个数;
(2)利用计算机或计算器产生整数随机数,然后n个整数随机数作为一组分组.每组第1个数表示第1次试验,第2个数表示第2次试验,第3个数表示第3次试验,…,第n个数表示第n次试验.n个随机数作为一组共组成N组数;
(3)统计这N组数中恰有k个数字在表示试验发生的数组中的组数m.
则n次重复试验中事件A恰好发生k次的概率近似为 .当堂检测探究一探究二探究三思维辨析变式训练3一个袋中有7个大小、形状相同的小球,6个白球,1个红球,现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取,试设计一个模拟试验,计算恰好第三次摸到红球的概率.
解用1,2,3,4,5,6表示白球,7表示红球,利用计算器或计算机产生1到7之间(包括1和7)取整数值的随机数.因为要求恰好第三次摸到红球的概率,所以每三个随机数作为一组.如下,产生20组随机数:
666 743 671 464 571
561 156 567 732 375
716 116 614 445 117
573 552 274 114 662
就相当于做了20次试验,在这些数组中,前两个数字不是7,第三个数字恰好是7就表示第一次、第二次摸到的是白球,第三次摸到的是红球,它们分别是567和117,共两组,因此恰好第三次摸到红球的概率约为当堂检测探究一探究二探究三思维辨析不理解随机数的意义,弄错随机数的范围而致误
典例 同时抛掷两枚质地均匀的骰子,用随机模拟法求所得点数之和是偶数的概率.
错解(1)用计算器产生1~10之间取整数值的随机数.
(2)统计所产生的随机数总个数N.
(3)把所产生的随机数两两分组,再相加,统计和是偶数的个数N1.
(4) 即是点数之和是偶数的概率近似值.
以上错解中都有哪些错误?出错的原因是什么?你如何订正?你如何防范?
错因分析骰子的点数为1~6之间的整数,故随机数的范围应设为1~6,并且每个数代表骰子出现的点数.错解中,没有理解随机数产生范围的含义,错误地把随机数的范围当作1~10,因此所求结果是错的.当堂检测探究一探究二探究三思维辨析正解抛掷两枚骰子,可以看作一枚骰子抛掷两次,用两个随机数字作为一组即可.
(1)抛掷一次只能出现6个等可能基本事件,所以用1~6之间的数字进行标注.
(2)用计算器或计算机产生1~6之间的取整数值的随机数,并用两个随机数值作为一组.
(3)统计随机数总组数N及两个随机数之和为偶数的组数N1.则所得点数之和为偶数的频率值就是 .
当模拟次数足够大时,可用频率近似作概率值,即所求概率约为 .
防范措施1.明确随机数的取值范围.
2.该种模拟用于试验结果是有限个的情况,每次模拟得到的近似概率不一定相同.当堂检测1.用计算机随机模拟方法估计概率时,其准确程度取决于( )
A.产生的随机数的大小 B.产生的随机数的个数
C.随机数对应的结果 D.产生随机数的方法
解析:随机数容量越大,概率越接近实际数.
答案:B探究一探究二探究三思维辨析当堂检测2.用计算器或计算机随机模拟掷质地均匀的骰子的试验,估计出现2点的概率,下列步骤中,不正确的是( )
A.用计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生6个不同的1到6之间的取整数值的随机数x,如果x=2,我们认为出现2点
B.我们通常用计数器n记录做了多少次掷骰子试验,用计数器m记录其中有多少次出现2点,掷n=0,m=0
C.出现2点,则m的值加1,即m=m+1;否则m的值保持不变
D.程序结束,出现2点的频率 作为概率的近似值
解析:计算器的随机函数RANDI(1,7)或计算机的随机函数RANDBETWEEN(1,7)产生的是1到7之间的整数,包括7,共7个整数,而骰子只有6个面,A不正确,故选A.
答案:A探究一探究二探究三思维辨析当堂检测3.抛掷一枚质地均匀的骰子两次,用随机模拟方法估计朝上面的点数和为8的概率,共进行了两次试验,第一次产生了60组随机数,第二次产生了200组随机数,那么这两次估计的结果相比较,第 次准确.?
解析:用随机模拟方法估计概率时,产生的随机数组数越多,估计的结果越准确,所以第二次比第一次准确.
答案:二探究一探究二探究三思维辨析当堂检测
