高中数学人教A版必修三课件 3章 模块复习课 第3课时 概率 :65张PPT
文档属性
| 名称 | 高中数学人教A版必修三课件 3章 模块复习课 第3课时 概率 :65张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:26:15 | ||
图片预览







文档简介
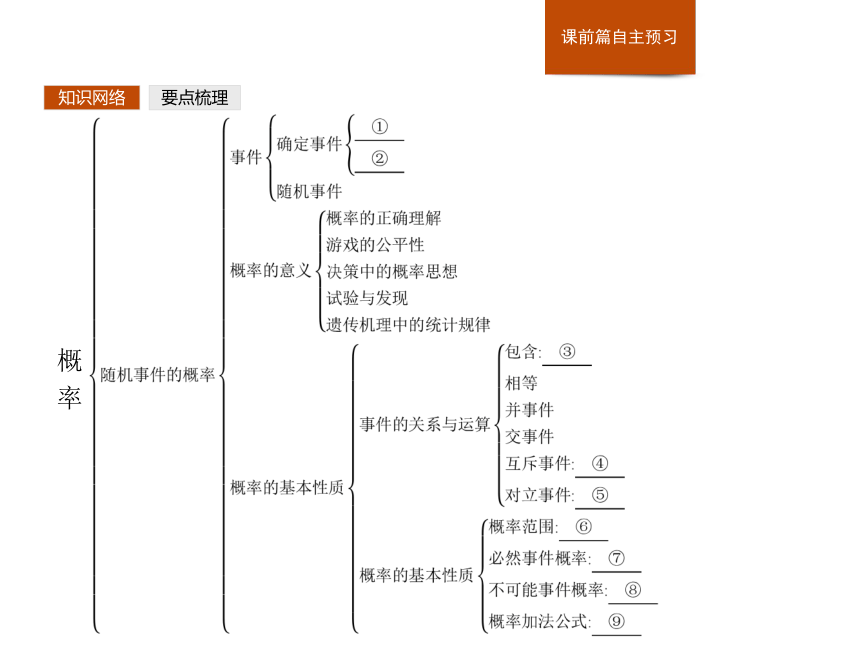
课件65张PPT。第3课时 概率知识网络要点梳理概
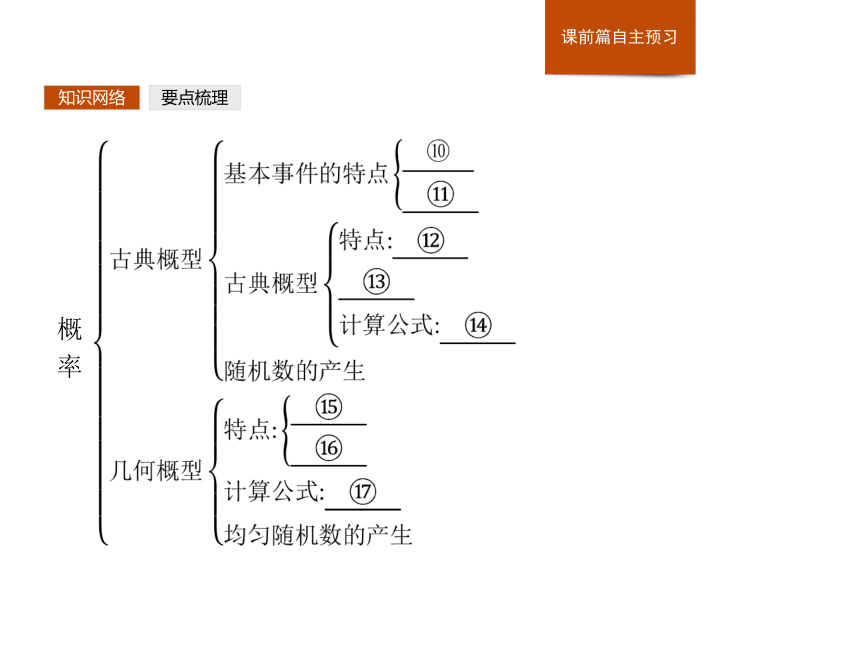
率 知识网络概
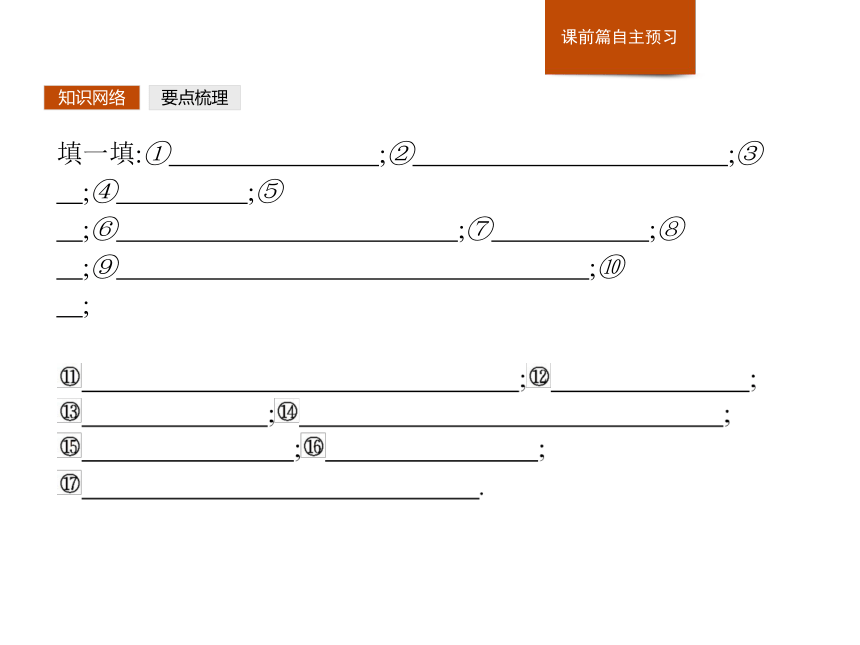
率 要点梳理知识网络填一填:① ;② ;③ ;④ ;⑤ ;⑥ ;⑦ ;⑧ ;⑨ ;⑩ ;要点梳理知识网络要点梳理知识网络1.什么是必然事件?什么是不可能事件?什么是随机事件?
提示必然事件:在一定条件下,一定会发生的事件.
不可能事件:在一定条件下,一定不会发生的事件.
随机事件:在一定条件下,可能发生也可能不发生的事件.要点梳理知识网络2.什么是频率?什么是概率?概率的取值范围是多少?频率与概率之间有什么关系?
提示在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例 为事件A出现的频率.对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率,简称为A的概率.概率的取值范围:0≤P(A)≤1.
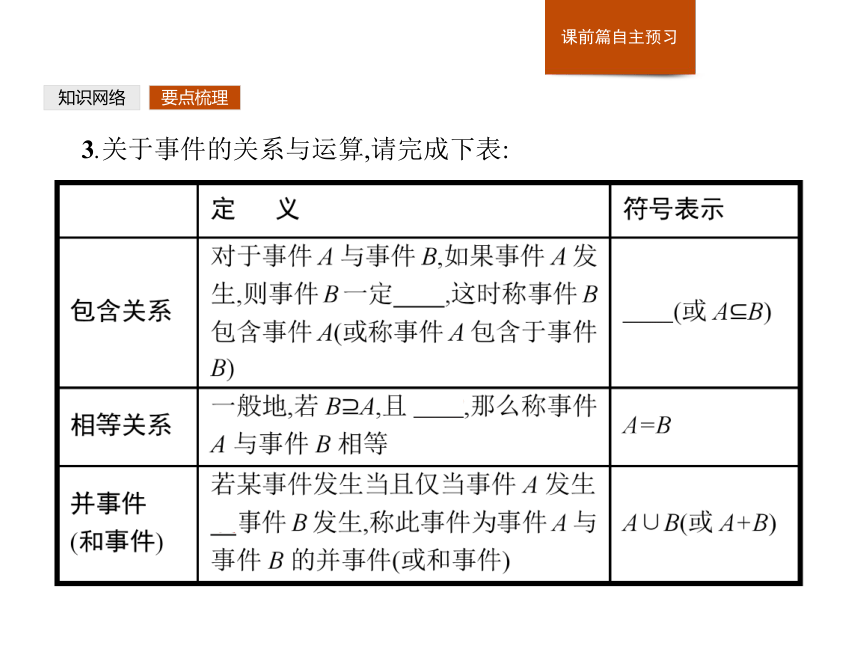
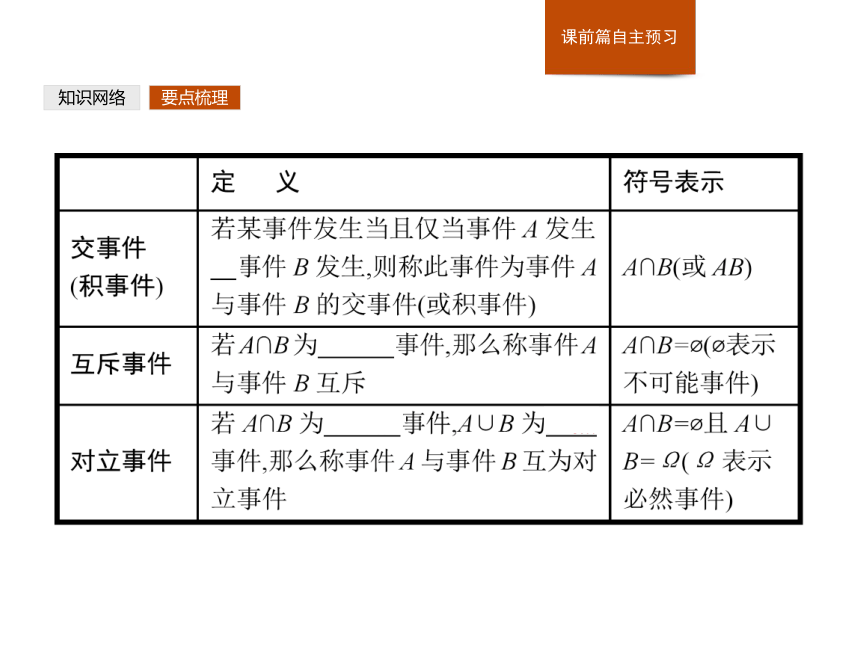
频率与概率之间的关系是:频率随着试验次数的变化而变化,概率却是一个常数,它是频率的科学抽象.当试验次数越来越多时,频率向概率靠近,只要次数足够多,所得频率就可以近似地当作随机事件的概率.要点梳理知识网络3.关于事件的关系与运算,请完成下表: 要点梳理知识网络要点梳理知识网络4.互斥事件和对立事件有什么区别和联系?
提示互斥事件和对立事件都是针对两个事件而言的.在一次试验中,两个互斥的事件有可能都不发生,也可能有一个发生;而两个对立的事件则必有一个发生,但不可能同时发生.所以,两个事件互斥,它们未必对立;两个事件对立,它们一定互斥.也就是说,两事件对立是两事件互斥的一种特殊情况.
5.互斥事件的概率加法公式怎样?对立事件的呢?
提示若事件A与事件B互斥,则P(A∪B)=P(A)+P(B).
若事件B与事件A互为对立事件,则P(A)=1-P(B).要点梳理知识网络6.什么是古典概型?古典概型有哪两个特点?古典概型的计算公式怎样?
提示具有以下两个特点的概率模型称为古典概率模型,简称为古典概型.古典概型的两个特点:(1)试验中所有可能出现的基本事件只有有限个;(2)每个基本事件出现的可能性相等.计算公式:
要点梳理知识网络7.什么是几何概型?几何概型有哪两个特点?几何概型的计算公式怎样?
提示如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.几何概型的两个特点:(1)试验中所有可能出现的基本事件具有无限个;(2)每个基本事件出现的可能性相等.计算公式:8.几何概型与古典概型有何异同?
提示相同点:古典概型与几何概型中基本事件发生的可能性都是相等的;求解的思路是相同的,同属“比例解法”.
不同点:古典概型中基本事件的个数是有限的,而几何概型中基本事件的个数是无限的,需用相应的几何度量求解.要点梳理知识网络思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)“方程x2+2x+8=0有两个实根”是不可能事件.( )
(2)不可能事件就是一定不会发生的事件.( )
(3)在大量重复试验中,概率是频率的稳定值.( )
(4)对立事件一定是互斥事件,互斥事件不一定是对立事件.( )
(5)一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是“至多有一次中靶”.( )
(6)两个事件的和事件是指两个事件都得发生.( )
(7)“在适宜条件下,种下一粒种子观察它是否发芽”属于古典概型,其基本事件是“发芽与不发芽”.( )要点梳理知识网络(8)掷一枚均匀硬币两次,出现“两个正面”“一正一反”“两个反面”,这三个结果是等可能事件.( )
(9)在古典概型中,如果事件A中基本事件构成集合A,所有的基本事件构成集合I,则事件A的概率为card(A)card(I).( )
(10)几何概型中,每一个基本事件就是从某个特定的几何区域内随机地取一点,该区域中的每一点被取到的机会相等.( )
(11)在几何概型定义中的区域可以是线段、平面图形、立体图形.( )
(12)与面积有关的几何概型的概率与几何图形的形状有关.( )
答案:(1)√ (2)√ (3)√ (4)√ (5)× (6)× (7)× (8)× (9)√ (10)√ (11)√ (12)×要点梳理专题归纳高考体验专题一 互斥事件与对立事件
1.互斥事件是不可能同时发生的两个事件;对立事件除要求这两个事件不同时发生外,还要求二者必须有一个发生.因此对立事件一定是互斥事件,但互斥事件不一定是对立事件,对立事件是互斥事件的特殊情况.
2.利用集合的观点来判断:设事件A与B所含的结果组成的集合分别是A,B,全集为I.
(1)事件A与B互斥,即集合A∩B=?;
(2)事件A与B对立,即集合A∩B=?,且A∪B=I,也即A=?IB,B=?IA;
(3)对互斥事件A与B的和A+B,可理解为集合A∪B.专题归纳高考体验3.若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
应用互斥事件的概率加法公式解题时,一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求其对立事件的概率.专题归纳高考体验例1 在某一时期内,一条河流某处的年最高水位值(单位:m)在各个范围内的概率如下表:
计算在同一时期内,河流此处的年最高水位值在下列范围内的概率:
(1)[10,16);(2)[8,12);(3)[14,18).
分析正确表示出各个事件并判断是互斥事件,利用加法公式求解.专题归纳高考体验解:记该河流某处的年最高水位值(单位:m)在[8,10),[10,12),[12,14),[14,16),[16,18)范围内分别为事件A,B,C,D,E,它们彼此互斥.
(1)P(B∪C∪D)=P(B)+P(C)+P(D)=0.28+0.38+0.16=0.82.
(2)P(A∪B)=P(A)+P(B)=0.1+0.28=0.38.
(3)P(D∪E)=P(D)+P(E)=0.16+0.08=0.24.
所以年最高水位值在[10,16),[8,12),[14,18)范围内的概率分别为0.82,0.38,0.24.专题归纳高考体验跟踪训练1甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?
(2)甲、乙两人中至少有一人抽到选择题的概率是多少?
解:把3个选择题记为x1,x2,x3,2个判断题记为p1,p2.总的事件数为20.
“甲抽到选择题,乙抽到判断题”的情况有:(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2),共6种;
“甲抽到判断题,乙抽到选择题”的情况有:(p1,x1),(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3),共6种;
“甲、乙都抽到选择题”的情况有:(x1,x2),(x1,x3),(x2,x1),(x2,x3),(x3,x1),(x3,x2),共6种;
“甲、乙都抽到判断题”的情况有:(p1,p2),(p2,p1),共2种.专题归纳高考体验专题归纳高考体验专题二 古典概型问题
古典概型是一种最基本的概型,也是学习其他概型的基础,要掌握古典概型的两个基本特征,即有限性和等可能性.在应用公式P(A)= 时,关键是要正确理解基本事件与事件A的关系,从而求出n,m.在求基本事件的总数时,可以用列举法、列图表或设有序数对的方法来求解.专题归纳高考体验例2某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长T(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
(1)求图中m的值;
(2)估计该校担任班主任的教师月平均通话时长的中位数;
(3)在[450,500),[500,550]这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.专题归纳高考体验分析(1)根据频率分布直方图中所有矩形的面积和为1,列出方程,即可求解;(2)设该校担任班主任的教师月平均通话时长的中位数为t,根据频率分布直方图的中位数的计算方法,即可求解;(3)根据分层抽样,可得在[450,500)内抽取4人,分别记为a,b,c,d,在[500,550]内抽取2人,记为e,f,利用古典概型及其概率的计算公式,即可求解.
解:(1)依题意,根据频率分布直方图的性质,可得:
50×(m+0.004 0+0.005 0+0.006 6+0.001 6+0.000 8)=1,解得m=0.002 0.
(2)设该校担任班主任的教师月平均通话时长的中位数为t.
因为前2组的频率之和为(0.002 0+0.004 0)×50=0.3<0.5,
前3组的频率之和为(0.002 0+0.004 0+0.005 0)×50=0.55>0.5,
所以350所以该校担任班主任的教师月平均通话时长的中位数为390分钟.专题归纳高考体验分别记为a,b,c,d,
在[500,550]内抽取2人,记为e,f,
则6人中抽取2人的取法有:{a,b},{a,c},{a,d},{a,e},{a,f},{b,c},{b,d},{b,e},{b,f},{c,d},{c,e},{c,f},{d,e},{d,f},{e,f},共15种等可能的取法.
其中抽取的2人恰在同一组的有{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},{e,f},共7种取法,所以从这6人中随机抽取的2人恰在同一组的概率专题归纳高考体验跟踪训练2一个均匀的正四面体面上分别涂有1,2,3,4四个数字,现在随机投掷两次,正四面体面朝下的数字分别为b,c.
(1)记z=(b-3)2+(c-3)2,求z=4的概率;
(2)若方程x2-bx-c=0至少有一根x∈{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.
解:(1)因为是投掷两次,因此基本事件是(b,c),有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个基本事件.专题归纳高考体验专题归纳高考体验专题三 几何概型问题
若试验同时具有基本事件个数的无限性和每个事件发生的等可能性两个特征,则此试验为几何概型,由于基本事件个数的无限性,其概率就不能应用 求解,因此需转化为几何度量(如长度、面积、体积等)的比值求解.
几何概型的三种类型分别为长度型、面积型和体积型,在解题时要准确把握,要把实际问题作合理的转化,特别是当涉及两个变量的取值范围时,一般是面积型几何概型,通常建立坐标系求解.专题归纳高考体验例3 将长为l的绳子随机剪成三段,求三段能构成三角形的概率.
分析利用几何概型求解.
解:记事件A为“三段能构成三角形”.
设x,y分别表示其中两段的长度,则第三段的长度为l-x-y.
则试验的全部结果可构成区域Ω:
{(x,y)|0解:设“弦长超过圆内接等边三角形的边长”为事件A.
在以半径为 的圆内任取一点P的结果有无限个,属于几何概型.
如图,△BCD是圆内接等边三角形.再作△BCD的内切圆,则满足“弦长超过圆内接等边三角形边长”的点P在等边三角形BCD的内切圆内.专题归纳高考体验专题归纳高考体验专题四 概率与统计的综合问题
概率与统计相结合,是新课标数学高考试题的一个亮点,其中所涉及的统计知识是基础知识,所涉及的概率是古典概型,虽然是综合题,但是难度不大,属于中档以下难度的题.专题归纳高考体验例4某校团委组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名学生,在实践活动结束后,学校团委对该班的所有学生都进行了测评,该班的A,B两个小组所有学生所得分数(百分制)的茎叶图如图所示,其中B组一学生的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.
(1)若在B组学生中随机挑选1人,求其得分超过85分的概率;
(2)现从A组这5名学生中随机抽取2名学生,设其分数分别为m,n,求|m-n|≤8的概率.
分析(1)利用统计的公式计算.专题归纳高考体验专题归纳高考体验跟踪训练4某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
?
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.专题归纳高考体验(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10 000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01).
分析(1)记B表示事件“一件这种产品为二等品”,C表示事件“一件这种产品为一等品”,则事件B,C互斥,且由频率分布直方图估计P(B),P(C),用公式P(A)=P(B+C)估计出事件A的概率;(2)由(1)可以求出任取一件产品是一等品、二等品的概率估计值,任取一件产品是三等品的概率估计值,这样可以求出10 000件产品估计有一等品、二等品、三等品的数量,最后估计出利润;(3)求出质量指标值M<90的频率和质量指标值M<100的频率,这样可以求出质量指标值M的中位数估计值.专题归纳高考体验解:(1)记B表示事件“一件这种产品为二等品”,C表示事件“一件这种产品为一等品”,
则事件B,C互斥,
且由频率分布直方图估计P(B)=0.2+0.3+0.15=0.65,P(C)=0.1+0.09=0.19,
又P(A)=P(B+C)=P(B)+P(C)=0.84,
所以事件A的概率估计为0.84.
(2)由(1)知,任取一件产品是一等品、二等品的概率估计值分别为0.19,0.65,
故任取一件产品是三等品的概率估计值为0.16,
从而10 000件产品估计有一等品、二等品、三等品分别为1 900,6 500,1 600件,故利润估计为1 900×10+6 500×6+1 600×2=61 200元.专题归纳高考体验(3)因为在产品质量指标值M的频率分布直方图中,
质量指标值M<90的频率为0.06+0.1+0.2=0.36<0.5,质量指标值M<100的频率为0.06+0.1+0.2+0.3=0.66>0.5,故质量指标值M的中位数估计值为专题归纳高考体验考点一:频率与概率的关系
1.(2019全国2高考)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 .?
解析:由题意,得经停该高铁站的列车的正点数约为10×0.97+20×0.98+10×0.99=39.2,其中车次数为10+20+10=40,所以经停该站高铁列车所有车次的平均正点率的估计值为
答案:0.98专题归纳高考体验2.(2017全国3高考)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:专题归纳高考体验以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
解:(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为 ,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.专题归纳高考体验(2)当这种酸奶一天的进货量为450瓶时,
若最高气温不低于25,
则Y=6×450-4×450=900;
若最高气温位于区间[20,25),
则Y=6×300+2(450-300)-4×450=300;
若最高气温低于20,
则Y=6×200+2(450-200)-4×450=-100.
所以,Y的所有可能值为900,300,-100.
Y大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为
因此Y大于零的概率的估计值为0.8.专题归纳高考体验3.(2016全国甲高考)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:专题归纳高考体验(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
解:(1)事件A发生当且仅当一年内出险次数小于2.
由所给数据知,一年内出险次数小于2的频率为 ,故P(A)的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.
由所给数据知,一年内出险次数大于1且小于4的频率为 =0.3,故P(B)的估计值为0.3.专题归纳高考体验(3)由所给数据得
调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.
因此,续保人本年度平均保费的估计值为1.192 5a.专题归纳高考体验考点二:古典概型
4.(2019全国2高考)生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为( )
解析:设测量过该指标的3只兔子为a,b,c,剩余2只为A,B,则从这5只兔子中任取3只的所有取法有{a,b,c},{a,b,A},{a,b,B},{a,c,A},{a,c,B},{a,A,B},{b,c,A},{b,c,B},{c,A,B},{b,A,B}共10种,其中恰有2只测量过该指标的取法有{a,b,A},{a,b,B},{a,c,A},{a,c,B},{b,c,A},{b,c,B}共6种,所以恰有2只测量过该指标的概率为
答案:B专题归纳高考体验5.(2018全国2高考)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 ( )
A.0.6 B.0.5 C.0.4 D.0.3
解析:设2名男同学为男1,男2,3名女同学为女1,女2,女3,则任选两人共有(男1,女1),(男1,女2),(男1,女3),(男1,男2),(男2,女1),(男2,女2)(男2,女3)(女1,女2),(女1,女3),(女2,女3)共10种,其中选中两人都为女同学共(女1,女2),(女1,女3)、(女2,女3)3种,故
答案:D专题归纳高考体验6.(2017全国2高考)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )专题归纳高考体验解析:由题意可得抽取两张卡片上的数的所有情况如下表所示(表中点的横坐标表示第一次取到的数,纵坐标表示第二次取到的数):
总共有25种情况,其中第一张卡片上的数大于第二张卡片上的数的情况有10种,故所求的概率为
答案:D专题归纳高考体验7.(2016全国乙高考)为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是 ( )
解析:总的基本事件是:红黄,白紫;红白,黄紫;红紫,黄白,共3种.满足条件的基本事件是:红黄,白紫;红白,黄紫,共2种.故所求事件的概率为
答案:C专题归纳高考体验8.(2016全国丙高考)小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( )
解析:密码的前两位共有15种可能,其中只有1种是正确的密码,因此所求概率为 .故选C.
答案:C专题归纳高考体验9.(2018天津高考)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.专题归纳高考体验解(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.
(2)①从抽出的7名同学中随机抽取2名同学的所有可能结果为
{A,B},{A,C},{A,D},{A,E},{A,F},{A,G},{B,C},{B,D},{B,E},{B,F},{B,G},{C,D},{C,E},{C,F},{C,G},{D,E},{D,F},{D,G},{E,F},{E,G},{F,G},共21种.
②由(1),不妨设抽出的7名同学中,来自甲年级的是A,B,C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A,B},{A,C},{B,C},{D,E},{F,G},共5种.
所以,事件M发生的概率专题归纳高考体验考点三:几何概型
10.(2018全国1高考)下图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则( )
A.p1=p2
B.p1=p3
C.p2=p3
D.p1=p2+p3专题归纳高考体验答案:A 专题归纳高考体验11.(2017全国1高考)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )答案:B 专题归纳高考体验12.(2016全国甲高考)某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )答案:B 专题归纳高考体验13.(2016全国甲高考)从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为 ( )
答案:C专题归纳高考体验考点四:概率与统计的综合
14.(2019天津高考)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.专题归纳高考体验①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.专题归纳高考体验解:(1)由已知,老、中、青员工人数之比为6∶9∶10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.
②由表格知,符合题意的所有可能结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},
{E,F},共11种.专题归纳高考体验15.(2019北京高考)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1 000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:专题归纳高考体验(1)估计该校学生中上个月A,B两种支付方式都使用的人数;
(2)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2 000元的概率;
(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2 000元.结合(2)的结果,能否认为样本仅使用B的学生中本月支付金额大于2 000 元的人数有变化?说明理由.专题归纳高考体验解:(1)由题知,样本中仅使用A的学生有27+3=30人,仅使用B的学生有24+1=25人,A,B两种支付方式都不使用的学生有5人.
故样本中A,B两种支付方式都使用的学生有100-30-25-5=40人.
估计该校学生中上个月A,B两种支付方式都使用的人数为 ×1 000=400.
(2)记事件C为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于2 000元”,则P(C)= =0.04.专题归纳高考体验(3)记事件E为“从样本仅使用B的学生中随机抽查1人,该学生本月的支付金额大于2 000元”.
假设样本仅使用B的学生中,本月支付金额大于2 000 元的人数没有变化,则由(2)知,P(E)=0.04.
答案示例1:可以认为有变化.理由如下:
P(E)比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月支付金额大于2 000元的人数发生了变化.所以可以认为有变化.
答案示例2:无法确定有没有变化.理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的.所以无法确定有没有变化.
率 知识网络概
率 要点梳理知识网络填一填:① ;② ;③ ;④ ;⑤ ;⑥ ;⑦ ;⑧ ;⑨ ;⑩ ;要点梳理知识网络要点梳理知识网络1.什么是必然事件?什么是不可能事件?什么是随机事件?
提示必然事件:在一定条件下,一定会发生的事件.
不可能事件:在一定条件下,一定不会发生的事件.
随机事件:在一定条件下,可能发生也可能不发生的事件.要点梳理知识网络2.什么是频率?什么是概率?概率的取值范围是多少?频率与概率之间有什么关系?
提示在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数nA为事件A出现的频数,称事件A出现的比例 为事件A出现的频率.对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率fn(A)稳定在某个常数上,把这个常数记作P(A),称为事件A的概率,简称为A的概率.概率的取值范围:0≤P(A)≤1.
频率与概率之间的关系是:频率随着试验次数的变化而变化,概率却是一个常数,它是频率的科学抽象.当试验次数越来越多时,频率向概率靠近,只要次数足够多,所得频率就可以近似地当作随机事件的概率.要点梳理知识网络3.关于事件的关系与运算,请完成下表: 要点梳理知识网络要点梳理知识网络4.互斥事件和对立事件有什么区别和联系?
提示互斥事件和对立事件都是针对两个事件而言的.在一次试验中,两个互斥的事件有可能都不发生,也可能有一个发生;而两个对立的事件则必有一个发生,但不可能同时发生.所以,两个事件互斥,它们未必对立;两个事件对立,它们一定互斥.也就是说,两事件对立是两事件互斥的一种特殊情况.
5.互斥事件的概率加法公式怎样?对立事件的呢?
提示若事件A与事件B互斥,则P(A∪B)=P(A)+P(B).
若事件B与事件A互为对立事件,则P(A)=1-P(B).要点梳理知识网络6.什么是古典概型?古典概型有哪两个特点?古典概型的计算公式怎样?
提示具有以下两个特点的概率模型称为古典概率模型,简称为古典概型.古典概型的两个特点:(1)试验中所有可能出现的基本事件只有有限个;(2)每个基本事件出现的可能性相等.计算公式:
要点梳理知识网络7.什么是几何概型?几何概型有哪两个特点?几何概型的计算公式怎样?
提示如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.几何概型的两个特点:(1)试验中所有可能出现的基本事件具有无限个;(2)每个基本事件出现的可能性相等.计算公式:8.几何概型与古典概型有何异同?
提示相同点:古典概型与几何概型中基本事件发生的可能性都是相等的;求解的思路是相同的,同属“比例解法”.
不同点:古典概型中基本事件的个数是有限的,而几何概型中基本事件的个数是无限的,需用相应的几何度量求解.要点梳理知识网络思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)“方程x2+2x+8=0有两个实根”是不可能事件.( )
(2)不可能事件就是一定不会发生的事件.( )
(3)在大量重复试验中,概率是频率的稳定值.( )
(4)对立事件一定是互斥事件,互斥事件不一定是对立事件.( )
(5)一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是“至多有一次中靶”.( )
(6)两个事件的和事件是指两个事件都得发生.( )
(7)“在适宜条件下,种下一粒种子观察它是否发芽”属于古典概型,其基本事件是“发芽与不发芽”.( )要点梳理知识网络(8)掷一枚均匀硬币两次,出现“两个正面”“一正一反”“两个反面”,这三个结果是等可能事件.( )
(9)在古典概型中,如果事件A中基本事件构成集合A,所有的基本事件构成集合I,则事件A的概率为card(A)card(I).( )
(10)几何概型中,每一个基本事件就是从某个特定的几何区域内随机地取一点,该区域中的每一点被取到的机会相等.( )
(11)在几何概型定义中的区域可以是线段、平面图形、立体图形.( )
(12)与面积有关的几何概型的概率与几何图形的形状有关.( )
答案:(1)√ (2)√ (3)√ (4)√ (5)× (6)× (7)× (8)× (9)√ (10)√ (11)√ (12)×要点梳理专题归纳高考体验专题一 互斥事件与对立事件
1.互斥事件是不可能同时发生的两个事件;对立事件除要求这两个事件不同时发生外,还要求二者必须有一个发生.因此对立事件一定是互斥事件,但互斥事件不一定是对立事件,对立事件是互斥事件的特殊情况.
2.利用集合的观点来判断:设事件A与B所含的结果组成的集合分别是A,B,全集为I.
(1)事件A与B互斥,即集合A∩B=?;
(2)事件A与B对立,即集合A∩B=?,且A∪B=I,也即A=?IB,B=?IA;
(3)对互斥事件A与B的和A+B,可理解为集合A∪B.专题归纳高考体验3.若事件A1,A2,A3,…,An彼此互斥,则P(A1∪A2∪…∪An)=P(A1)+P(A2)+…+P(An).
应用互斥事件的概率加法公式解题时,一定要注意首先确定各个事件是否彼此互斥,然后求出各事件分别发生的概率,再求和.对于较复杂事件的概率,可以转化为求其对立事件的概率.专题归纳高考体验例1 在某一时期内,一条河流某处的年最高水位值(单位:m)在各个范围内的概率如下表:
计算在同一时期内,河流此处的年最高水位值在下列范围内的概率:
(1)[10,16);(2)[8,12);(3)[14,18).
分析正确表示出各个事件并判断是互斥事件,利用加法公式求解.专题归纳高考体验解:记该河流某处的年最高水位值(单位:m)在[8,10),[10,12),[12,14),[14,16),[16,18)范围内分别为事件A,B,C,D,E,它们彼此互斥.
(1)P(B∪C∪D)=P(B)+P(C)+P(D)=0.28+0.38+0.16=0.82.
(2)P(A∪B)=P(A)+P(B)=0.1+0.28=0.38.
(3)P(D∪E)=P(D)+P(E)=0.16+0.08=0.24.
所以年最高水位值在[10,16),[8,12),[14,18)范围内的概率分别为0.82,0.38,0.24.专题归纳高考体验跟踪训练1甲、乙两人参加普法知识竞赛,共有5个不同的题目.其中,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)甲、乙两人中有一个抽到选择题,另一个抽到判断题的概率是多少?
(2)甲、乙两人中至少有一人抽到选择题的概率是多少?
解:把3个选择题记为x1,x2,x3,2个判断题记为p1,p2.总的事件数为20.
“甲抽到选择题,乙抽到判断题”的情况有:(x1,p1),(x1,p2),(x2,p1),(x2,p2),(x3,p1),(x3,p2),共6种;
“甲抽到判断题,乙抽到选择题”的情况有:(p1,x1),(p1,x2),(p1,x3),(p2,x1),(p2,x2),(p2,x3),共6种;
“甲、乙都抽到选择题”的情况有:(x1,x2),(x1,x3),(x2,x1),(x2,x3),(x3,x1),(x3,x2),共6种;
“甲、乙都抽到判断题”的情况有:(p1,p2),(p2,p1),共2种.专题归纳高考体验专题归纳高考体验专题二 古典概型问题
古典概型是一种最基本的概型,也是学习其他概型的基础,要掌握古典概型的两个基本特征,即有限性和等可能性.在应用公式P(A)= 时,关键是要正确理解基本事件与事件A的关系,从而求出n,m.在求基本事件的总数时,可以用列举法、列图表或设有序数对的方法来求解.专题归纳高考体验例2某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长T(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.
(1)求图中m的值;
(2)估计该校担任班主任的教师月平均通话时长的中位数;
(3)在[450,500),[500,550]这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.专题归纳高考体验分析(1)根据频率分布直方图中所有矩形的面积和为1,列出方程,即可求解;(2)设该校担任班主任的教师月平均通话时长的中位数为t,根据频率分布直方图的中位数的计算方法,即可求解;(3)根据分层抽样,可得在[450,500)内抽取4人,分别记为a,b,c,d,在[500,550]内抽取2人,记为e,f,利用古典概型及其概率的计算公式,即可求解.
解:(1)依题意,根据频率分布直方图的性质,可得:
50×(m+0.004 0+0.005 0+0.006 6+0.001 6+0.000 8)=1,解得m=0.002 0.
(2)设该校担任班主任的教师月平均通话时长的中位数为t.
因为前2组的频率之和为(0.002 0+0.004 0)×50=0.3<0.5,
前3组的频率之和为(0.002 0+0.004 0+0.005 0)×50=0.55>0.5,
所以350
在[500,550]内抽取2人,记为e,f,
则6人中抽取2人的取法有:{a,b},{a,c},{a,d},{a,e},{a,f},{b,c},{b,d},{b,e},{b,f},{c,d},{c,e},{c,f},{d,e},{d,f},{e,f},共15种等可能的取法.
其中抽取的2人恰在同一组的有{a,b},{a,c},{a,d},{b,c},{b,d},{c,d},{e,f},共7种取法,所以从这6人中随机抽取的2人恰在同一组的概率专题归纳高考体验跟踪训练2一个均匀的正四面体面上分别涂有1,2,3,4四个数字,现在随机投掷两次,正四面体面朝下的数字分别为b,c.
(1)记z=(b-3)2+(c-3)2,求z=4的概率;
(2)若方程x2-bx-c=0至少有一根x∈{1,2,3,4},就称该方程为“漂亮方程”,求方程为“漂亮方程”的概率.
解:(1)因为是投掷两次,因此基本事件是(b,c),有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个基本事件.专题归纳高考体验专题归纳高考体验专题三 几何概型问题
若试验同时具有基本事件个数的无限性和每个事件发生的等可能性两个特征,则此试验为几何概型,由于基本事件个数的无限性,其概率就不能应用 求解,因此需转化为几何度量(如长度、面积、体积等)的比值求解.
几何概型的三种类型分别为长度型、面积型和体积型,在解题时要准确把握,要把实际问题作合理的转化,特别是当涉及两个变量的取值范围时,一般是面积型几何概型,通常建立坐标系求解.专题归纳高考体验例3 将长为l的绳子随机剪成三段,求三段能构成三角形的概率.
分析利用几何概型求解.
解:记事件A为“三段能构成三角形”.
设x,y分别表示其中两段的长度,则第三段的长度为l-x-y.
则试验的全部结果可构成区域Ω:
{(x,y)|0
在以半径为 的圆内任取一点P的结果有无限个,属于几何概型.
如图,△BCD是圆内接等边三角形.再作△BCD的内切圆,则满足“弦长超过圆内接等边三角形边长”的点P在等边三角形BCD的内切圆内.专题归纳高考体验专题归纳高考体验专题四 概率与统计的综合问题
概率与统计相结合,是新课标数学高考试题的一个亮点,其中所涉及的统计知识是基础知识,所涉及的概率是古典概型,虽然是综合题,但是难度不大,属于中档以下难度的题.专题归纳高考体验例4某校团委组织该校高中一年级某班以小组为单位利用周末时间进行了一次社会实践活动,且每个小组有5名学生,在实践活动结束后,学校团委对该班的所有学生都进行了测评,该班的A,B两个小组所有学生所得分数(百分制)的茎叶图如图所示,其中B组一学生的分数已被污损,但知道B组学生的平均分比A组学生的平均分高1分.
(1)若在B组学生中随机挑选1人,求其得分超过85分的概率;
(2)现从A组这5名学生中随机抽取2名学生,设其分数分别为m,n,求|m-n|≤8的概率.
分析(1)利用统计的公式计算.专题归纳高考体验专题归纳高考体验跟踪训练4某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
?
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.专题归纳高考体验(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10 000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01).
分析(1)记B表示事件“一件这种产品为二等品”,C表示事件“一件这种产品为一等品”,则事件B,C互斥,且由频率分布直方图估计P(B),P(C),用公式P(A)=P(B+C)估计出事件A的概率;(2)由(1)可以求出任取一件产品是一等品、二等品的概率估计值,任取一件产品是三等品的概率估计值,这样可以求出10 000件产品估计有一等品、二等品、三等品的数量,最后估计出利润;(3)求出质量指标值M<90的频率和质量指标值M<100的频率,这样可以求出质量指标值M的中位数估计值.专题归纳高考体验解:(1)记B表示事件“一件这种产品为二等品”,C表示事件“一件这种产品为一等品”,
则事件B,C互斥,
且由频率分布直方图估计P(B)=0.2+0.3+0.15=0.65,P(C)=0.1+0.09=0.19,
又P(A)=P(B+C)=P(B)+P(C)=0.84,
所以事件A的概率估计为0.84.
(2)由(1)知,任取一件产品是一等品、二等品的概率估计值分别为0.19,0.65,
故任取一件产品是三等品的概率估计值为0.16,
从而10 000件产品估计有一等品、二等品、三等品分别为1 900,6 500,1 600件,故利润估计为1 900×10+6 500×6+1 600×2=61 200元.专题归纳高考体验(3)因为在产品质量指标值M的频率分布直方图中,
质量指标值M<90的频率为0.06+0.1+0.2=0.36<0.5,质量指标值M<100的频率为0.06+0.1+0.2+0.3=0.66>0.5,故质量指标值M的中位数估计值为专题归纳高考体验考点一:频率与概率的关系
1.(2019全国2高考)我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为 .?
解析:由题意,得经停该高铁站的列车的正点数约为10×0.97+20×0.98+10×0.99=39.2,其中车次数为10+20+10=40,所以经停该站高铁列车所有车次的平均正点率的估计值为
答案:0.98专题归纳高考体验2.(2017全国3高考)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:专题归纳高考体验以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
解:(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为 ,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.专题归纳高考体验(2)当这种酸奶一天的进货量为450瓶时,
若最高气温不低于25,
则Y=6×450-4×450=900;
若最高气温位于区间[20,25),
则Y=6×300+2(450-300)-4×450=300;
若最高气温低于20,
则Y=6×200+2(450-200)-4×450=-100.
所以,Y的所有可能值为900,300,-100.
Y大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为
因此Y大于零的概率的估计值为0.8.专题归纳高考体验3.(2016全国甲高考)某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:专题归纳高考体验(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
解:(1)事件A发生当且仅当一年内出险次数小于2.
由所给数据知,一年内出险次数小于2的频率为 ,故P(A)的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.
由所给数据知,一年内出险次数大于1且小于4的频率为 =0.3,故P(B)的估计值为0.3.专题归纳高考体验(3)由所给数据得
调查的200名续保人的平均保费为0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=1.192 5a.
因此,续保人本年度平均保费的估计值为1.192 5a.专题归纳高考体验考点二:古典概型
4.(2019全国2高考)生物实验室有5只兔子,其中只有3只测量过某项指标.若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为( )
解析:设测量过该指标的3只兔子为a,b,c,剩余2只为A,B,则从这5只兔子中任取3只的所有取法有{a,b,c},{a,b,A},{a,b,B},{a,c,A},{a,c,B},{a,A,B},{b,c,A},{b,c,B},{c,A,B},{b,A,B}共10种,其中恰有2只测量过该指标的取法有{a,b,A},{a,b,B},{a,c,A},{a,c,B},{b,c,A},{b,c,B}共6种,所以恰有2只测量过该指标的概率为
答案:B专题归纳高考体验5.(2018全国2高考)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为 ( )
A.0.6 B.0.5 C.0.4 D.0.3
解析:设2名男同学为男1,男2,3名女同学为女1,女2,女3,则任选两人共有(男1,女1),(男1,女2),(男1,女3),(男1,男2),(男2,女1),(男2,女2)(男2,女3)(女1,女2),(女1,女3),(女2,女3)共10种,其中选中两人都为女同学共(女1,女2),(女1,女3)、(女2,女3)3种,故
答案:D专题归纳高考体验6.(2017全国2高考)从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )专题归纳高考体验解析:由题意可得抽取两张卡片上的数的所有情况如下表所示(表中点的横坐标表示第一次取到的数,纵坐标表示第二次取到的数):
总共有25种情况,其中第一张卡片上的数大于第二张卡片上的数的情况有10种,故所求的概率为
答案:D专题归纳高考体验7.(2016全国乙高考)为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是 ( )
解析:总的基本事件是:红黄,白紫;红白,黄紫;红紫,黄白,共3种.满足条件的基本事件是:红黄,白紫;红白,黄紫,共2种.故所求事件的概率为
答案:C专题归纳高考体验8.(2016全国丙高考)小敏打开计算机时,忘记了开机密码的前两位,只记得第一位是M,I,N中的一个字母,第二位是1,2,3,4,5中的一个数字,则小敏输入一次密码能够成功开机的概率是( )
解析:密码的前两位共有15种可能,其中只有1种是正确的密码,因此所求概率为 .故选C.
答案:C专题归纳高考体验9.(2018天津高考)已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(1)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(2)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.专题归纳高考体验解(1)由已知,甲、乙、丙三个年级的学生志愿者人数之比为3∶2∶2,由于采用分层抽样的方法从中抽取7名同学,因此应从甲、乙、丙三个年级的学生志愿者中分别抽取3人,2人,2人.
(2)①从抽出的7名同学中随机抽取2名同学的所有可能结果为
{A,B},{A,C},{A,D},{A,E},{A,F},{A,G},{B,C},{B,D},{B,E},{B,F},{B,G},{C,D},{C,E},{C,F},{C,G},{D,E},{D,F},{D,G},{E,F},{E,G},{F,G},共21种.
②由(1),不妨设抽出的7名同学中,来自甲年级的是A,B,C,来自乙年级的是D,E,来自丙年级的是F,G,则从抽出的7名同学中随机抽取的2名同学来自同一年级的所有可能结果为{A,B},{A,C},{B,C},{D,E},{F,G},共5种.
所以,事件M发生的概率专题归纳高考体验考点三:几何概型
10.(2018全国1高考)下图来自古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则( )
A.p1=p2
B.p1=p3
C.p2=p3
D.p1=p2+p3专题归纳高考体验答案:A 专题归纳高考体验11.(2017全国1高考)如图,正方形ABCD内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点,则此点取自黑色部分的概率是( )答案:B 专题归纳高考体验12.(2016全国甲高考)某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )答案:B 专题归纳高考体验13.(2016全国甲高考)从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),其中两数的平方和小于1的数对共有m个,则用随机模拟的方法得到的圆周率π的近似值为 ( )
答案:C专题归纳高考体验考点四:概率与统计的综合
14.(2019天津高考)2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人?
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.专题归纳高考体验①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.专题归纳高考体验解:(1)由已知,老、中、青员工人数之比为6∶9∶10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.
②由表格知,符合题意的所有可能结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},
{E,F},共11种.专题归纳高考体验15.(2019北京高考)改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1 000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:专题归纳高考体验(1)估计该校学生中上个月A,B两种支付方式都使用的人数;
(2)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2 000元的概率;
(3)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2 000元.结合(2)的结果,能否认为样本仅使用B的学生中本月支付金额大于2 000 元的人数有变化?说明理由.专题归纳高考体验解:(1)由题知,样本中仅使用A的学生有27+3=30人,仅使用B的学生有24+1=25人,A,B两种支付方式都不使用的学生有5人.
故样本中A,B两种支付方式都使用的学生有100-30-25-5=40人.
估计该校学生中上个月A,B两种支付方式都使用的人数为 ×1 000=400.
(2)记事件C为“从样本仅使用B的学生中随机抽取1人,该学生上个月的支付金额大于2 000元”,则P(C)= =0.04.专题归纳高考体验(3)记事件E为“从样本仅使用B的学生中随机抽查1人,该学生本月的支付金额大于2 000元”.
假设样本仅使用B的学生中,本月支付金额大于2 000 元的人数没有变化,则由(2)知,P(E)=0.04.
答案示例1:可以认为有变化.理由如下:
P(E)比较小,概率比较小的事件一般不容易发生,一旦发生,就有理由认为本月支付金额大于2 000元的人数发生了变化.所以可以认为有变化.
答案示例2:无法确定有没有变化.理由如下:
事件E是随机事件,P(E)比较小,一般不容易发生,但还是有可能发生的.所以无法确定有没有变化.
