高中数学北师大版必修五课件 第一章 数列1.4 数列在日常经济生活中的应用 :32张PPT
文档属性
| 名称 | 高中数学北师大版必修五课件 第一章 数列1.4 数列在日常经济生活中的应用 :32张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 554.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览











文档简介
课件32张PPT。§4 数列在日常经济生活中的应用1.储蓄利息的计算方法
(1)单利:单利的计算是仅在原有本金上计算利息,对本金所产生的利息不再计算利息.其公式为:利息=本金×利率×存期.
以符号P代表本金,n代表存期,r代表利率,S代表本金与利息和(以下简称本利和),则有S=P(1+nr).
(2)复利:把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的.复利的计算公式是S=P(1+r)n.
【做一做1】某人从2016年1月1日起,每年的这一天都到银行存一年定期存款a元,若年利率r保持不变,且每年到期的存款将本金和利息都再存入新一年的定期中,到2020年1月1日,将所有的存款、利息全部取回,他可取回的钱数为 .?2.三种银行储蓄业务模型
(1)“零存整取”模型
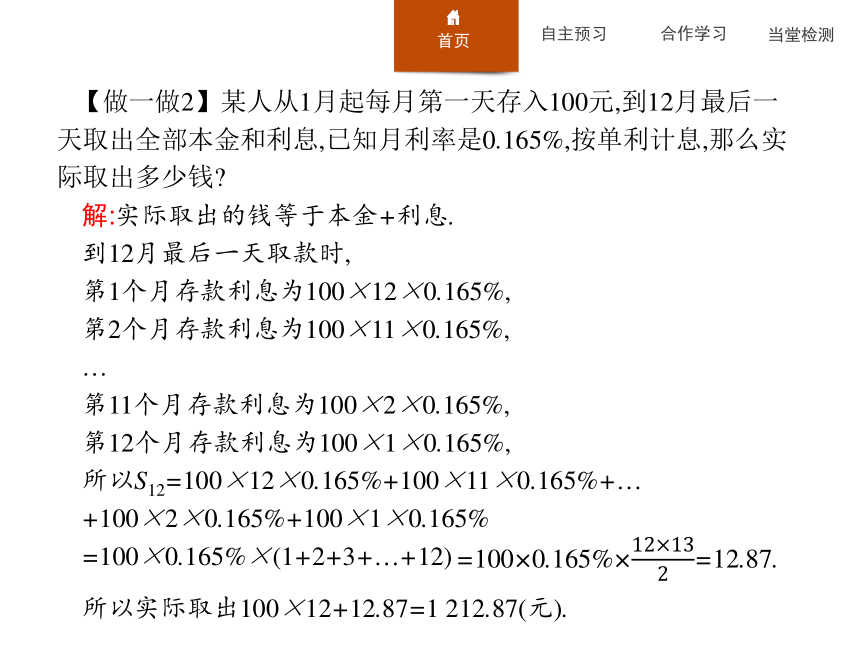
银行有一种叫作“零存整取”的储蓄业务,即每月定时存入一笔 相同数目的现金,这是零存;到约定日期,可以取出全部本利和,这是整取.规定每次存入的钱不计复利.(暂不考虑利息税) 【做一做2】某人从1月起每月第一天存入100元,到12月最后一天取出全部本金和利息,已知月利率是0.165%,按单利计息,那么实际取出多少钱??
解:实际取出的钱等于本金+利息.
到12月最后一天取款时,
第1个月存款利息为100×12×0.165%,
第2个月存款利息为100×11×0.165%,
…
第11个月存款利息为100×2×0.165%,
第12个月存款利息为100×1×0.165%,
所以S12=100×12×0.165%+100×11×0.165%+…
+100×2×0.165%+100×1×0.165%
=100×0.165%×(1+2+3+…+12)所以实际取出100×12+12.87=1 212.87(元).(2)“定期自动转存”模型
银行有另一种储蓄业务为“定期存款自动转存”.
例如,储户某日存入一笔1年期定期存款,1年后,如果储户不取出本利和,则银行自动办理转存业务,第2年的本金就是第1年的本利和.(3)“分期付款”模型
分期付款是一种新的付款方式,就是可以不一次性将款付清,就使用商品(或贷款),还款时可以分期将款逐步还清;
分期付款中,一般规定每次付款额相同,每期付款的时间间隔相同;
分期付款中,每月按利息复利计算,即上月(年)的利息要计入下月(年)的本金;
分期付款中,贷款(或商品价值)与每期付款额在贷款付清之前,会随时间推移而不断增值,即分期付款的总额高于一次性付款的总额;
分期所付的款连同到最后一次付款时所生的利息之和,等于商品售价及从购物到最后一次付款时的利息之和,即每期付款产生的本利和的累加与商品的付款总额相等,解决分期付款问题的数学方法就是等比数列求和.这也是等比数列在日常经济生活中的一个重要应用.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)银行储蓄中,本金与月利率均相同,存期1年,则使用复利计算应大于使用单利计算所得的本利和. ( )
(2)某产品计划每年成本降低m%,若三年后成本为a元,则现在成本是a(1+m%)3. ( )
(3)某工厂生产总值连续两年的年平均增长率依次为p%,q%,则这两年的平均增长率是 .( )
答案:(1)√ (2)× (3)√探究一探究二探究三规范解答
【例1】 某产品按质量分10个档次,生产最低档次的产品的利润是8元/件,每提高一个档次,利润每件增加2元,同时每提高一个档次,产量减少3件,在相同的时间内,最低档次的产品可生产60件.试问:在相同的时间内,应选择生产第几档次的产品可获得最大利润?(设最低档次为第1档次)
分析:由于总利润=第n档次的件数×第n档次每件的利润,因此需要求出第n档次的件数及第n档次的利润的表达式.探究一探究二探究三规范解答解:设在相同的时间内,从低到高每档次产品生产的件数分别为a1,a2,…,a10(单位:件),对应每档次产品的利润分别为b1,b2,…,b10(单位:元),则{an},{bn}均为等差数列,且a1=60,d=-3,b1=8,d'=2,
∴an=60-3(n-1)=-3n+63,
bn=8+2(n-1)=2n+6,
∴利润f(n)=anbn=(-3n+63)(2n+6)
=-6n2+108n+378=-6(n-9)2+864.
显然,当n=9时,f(n)max=f(9)=864元.
答:在相同的时间内,生产第9档次的产品可以获得最大利润.探究一探究二探究三规范解答反思感悟1.在实际问题中,若变化量在每次增加(或减少)的过程中不重复计算,增加(或减少)的量相同,且与正整数有关,则可以建立等差数列模型解决问题.
2.建立等差数列模型后,可以根据等差数列的通项公式an=a1+(n-1)d=am+(n-m)d与前n项和公式探究一探究二探究三规范解答 变式训练1 教育储蓄是一种零存整取的定期储蓄存款方式,它享受整存整取利率,利息免税.教育储蓄的对象为在校小学四年级(含四年级)以上的学生.假设零存整取3年期教育储蓄的月利率为2.325‰.按规定,3年期教育储蓄的存款总额不得超过2万元.?
(1)欲在3年后一次性支取本利和2万元,每月大约需存入多少元?
(2)零存整取3年期教育储蓄每月至多存入多少元?此时3年后本利和约为多少?(精确到1元)探究一探究二探究三规范解答解:(1)设每月存入A元,则有A(1+2.325‰)+A(1+2×2.325‰)+
…+A(1+36×2.325‰)=20 000.探究一探究二探究三规范解答(1)设n年内(本年度为第1年)总投入为an万元,旅游业总收入为bn万元,写出an,bn的表达式.
(2)至少经过几年旅游业的总收入将超过6 400万元?
分析: (1)从题意出发,从条件中提取有用的信息, 构造出等比数列,可用等比数列的前n项和公式求解. (2)令bn>6 400,解不等式即可.探究一探究二探究三规范解答探究一探究二探究三规范解答探究一探究二探究三规范解答反思感悟1.在实际问题中,若变化量每次增加(或减少)的百分数相同,且与正整数有关,则可以建立等比数列模型解决问题.
2.建立等比数列模型后,可利用等比数列的通项公式an=a1qn-1=amqn-m,前n项和公式探究一探究二探究三规范解答变式训练2某厂去年产值为a,计划在5年内每年比上一年产值增长10%,从今年起五年内这个工厂的总产值是( )
A.1.14 a B.1.15 a
C.10(1.15-1)a D.11(1.15-1)a
解析:由题意知,从今年起,这个工厂每年的产值构成以1.1a为首项,1.1为公比的等比数列.
答案:D探究一探究二探究三规范解答
【例3】小张老师年初向银行贷款2万元用于买车,银行贷款的年利率为10%,按复利计算.若这笔贷款要分10年等额还清,每年年初还一次,并且从借款后次年年初开始归还,问每年应还多少元?(精确到1元)
分析:从以下两点考虑:(1)每年按复利计算,即本年利息计入次年的本金生息;(2)分期付款,各期所付的款以及到最后一次付款时所生的利息合计,应等于2万元及2万元到最后一次付款时所生的利息之和.探究一探究二探究三规范解答解:设每年还款x元,需10年还清,则每年还款及利息情况如下:
第10年还款x元,此次欠款全部还清;
第9年还款x元,过1年欠款全部还清时,所付款连同利息之和为x(1+10%)元;
第8年还款x元,过2年欠款全部还清时,所付款连同利息之和为x(1+10%)2元;
……
第1年还款x元,过9年欠款全部还清时,所付款连同利息之和为x(1+10%)9元.
根据题意可得:
x+x(1+10%)+x(1+10%)2+…+x(1+10%)9=20 000(1+10%)10,∴每年应还款3 255元. 探究一探究二探究三规范解答反思感悟分期付款的相关规定:(1)分期付款中,每期的利息均按复利计算,分期付款中规定每期所付款额相同;(2)各期所付款额连同到最后一次付款时所产生的利息之和等于商品售价及从购买到最后一次付款时的利息之和(此为列方程的依据);(3)每期付款增值后的款数及售价增值后的款数均按S=P(1+r)n来计算,其中P代表本金(可以是每期付款额x,也可以是商品售价),n代表存期(月数或年数),r代表利率,S代表本利和.探究一探究二探究三规范解答变式训练3 某百货公司采用分期付款的办法销售家用空调机,售价为15 000元,分6个月付清,每月付一次,月利率以6%的单利计算,问购买者每月应付 元(不满1元的舍去).?
解析:设每月应付款为x元,则自第一月至付清本利合计为
x(1+0.06×5)+x(1+0.06×4)+…+x(1+0.06×1)+x
=x[6+0.06×(5+4+3+2+1)]=6.9x.
另一方面,15 000元在5个月的本利合计为
15 000(1+0.06×5)=19 500,6.9x=19 500,即x≈2 826(元).
答案:2 826探究一探究二探究三规范解答递推数列模型在实际中的应用
【典例】某地区位于沙漠边缘地区,人与沙漠进行长期不懈的斗争,到2014年底全地区的绿化率已达到30%,从2015年开始,每年将出现以下变化:原有沙漠面积的16%将栽上树,改造为绿洲,同时,原有绿洲面积的4%又被侵蚀,变为沙漠.分析:本题可以先建立递推数列关系,然后构造成所证明的数列结构,再间接求出an,进而求出所需年数.探究一探究二探究三规范解答探究一探究二探究三规范解答探究一探究二探究三规范解答反思提升如果某一个量,每一期以一个固定的百分数增加(或减少),或以一个固定的具体量增加(或减少)时,我们称这样的模型为生长模型,如分期付款、森林生长与砍伐、沙漠治理等问题就属于生长模型.探究一探究二探究三规范解答变式训练 一牧羊人赶着一群羊通过36个关口,每过一个关口,守关口人将拿走当时羊的一半,然后退还一只,过完这些关口后,牧羊人只剩下2只羊,问原来牧羊人赶了多少只羊??
解:设过第n关后牧羊人剩下an+1只羊,第n关前的羊数为an只,即2an+1=an+2(n=1,2,3,…).
由递推关系式得an=2(an+1-1),
将a36=2代入上式可得a35=a34=…=a1=2,
则a1即为牧羊人原来羊的只数2只.123451.有一套丛书共6册,计划2016年出版第一册,每两年出版一册,则出版齐这套丛书的年份是( )
A.2024 B.2026 C.2028 D.2029
解析:由已知得出版齐这套丛书的年份是2016+(6-1)×2=2026.
答案:B123452.某种细胞开始有2个,1小时后分裂成4个,2小时后分裂成8个,3小时后分裂成16个,……,按此规律,6小时后细胞的个数是( )
A.63 B.64 C.127 D.128
解析:细胞分裂的个数依次构成等比数列,
记为{an},则a1=2,公比q=2,
则a7=a1·q6=2×26=128.
答案:D123453.某种产品平均每三年价格降低 ,目前售价640元,则9年后此产品的价格为 元.?
解析:由题意知9年后的价格为
答案:270123454.夏季高山上气温从山脚起每升高100米降低约0.7 ℃,已知山顶气温是14.1 ℃,山脚的气温是26 ℃,则山顶相对于山脚的高度约是 米.?
解析:山顶气温与山脚气温相差26 ℃-14.1 ℃=11.9 ℃.
∵气温每升高100米降低约0.7 ℃,
∴山顶相对于山脚的高度约为
答案:1 700 123455.某渔场养鱼,第一年鱼的质量增长200%,以后每年的质量增长率是前一年增长率的一半.
(1)当饲养4年后,鱼的质量是原来的多少倍?
(2)如果由于某种原因,每年损失预计质量的10%,那么经过多少年后鱼的总质量开始减少?
解:(1)设鱼原来的质量为a,n年后鱼的质量为an,则
a1=(1+2)a=3a,a2=3a(1+1)=6a,
(1)单利:单利的计算是仅在原有本金上计算利息,对本金所产生的利息不再计算利息.其公式为:利息=本金×利率×存期.
以符号P代表本金,n代表存期,r代表利率,S代表本金与利息和(以下简称本利和),则有S=P(1+nr).
(2)复利:把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的.复利的计算公式是S=P(1+r)n.
【做一做1】某人从2016年1月1日起,每年的这一天都到银行存一年定期存款a元,若年利率r保持不变,且每年到期的存款将本金和利息都再存入新一年的定期中,到2020年1月1日,将所有的存款、利息全部取回,他可取回的钱数为 .?2.三种银行储蓄业务模型
(1)“零存整取”模型
银行有一种叫作“零存整取”的储蓄业务,即每月定时存入一笔 相同数目的现金,这是零存;到约定日期,可以取出全部本利和,这是整取.规定每次存入的钱不计复利.(暂不考虑利息税) 【做一做2】某人从1月起每月第一天存入100元,到12月最后一天取出全部本金和利息,已知月利率是0.165%,按单利计息,那么实际取出多少钱??
解:实际取出的钱等于本金+利息.
到12月最后一天取款时,
第1个月存款利息为100×12×0.165%,
第2个月存款利息为100×11×0.165%,
…
第11个月存款利息为100×2×0.165%,
第12个月存款利息为100×1×0.165%,
所以S12=100×12×0.165%+100×11×0.165%+…
+100×2×0.165%+100×1×0.165%
=100×0.165%×(1+2+3+…+12)所以实际取出100×12+12.87=1 212.87(元).(2)“定期自动转存”模型
银行有另一种储蓄业务为“定期存款自动转存”.
例如,储户某日存入一笔1年期定期存款,1年后,如果储户不取出本利和,则银行自动办理转存业务,第2年的本金就是第1年的本利和.(3)“分期付款”模型
分期付款是一种新的付款方式,就是可以不一次性将款付清,就使用商品(或贷款),还款时可以分期将款逐步还清;
分期付款中,一般规定每次付款额相同,每期付款的时间间隔相同;
分期付款中,每月按利息复利计算,即上月(年)的利息要计入下月(年)的本金;
分期付款中,贷款(或商品价值)与每期付款额在贷款付清之前,会随时间推移而不断增值,即分期付款的总额高于一次性付款的总额;
分期所付的款连同到最后一次付款时所生的利息之和,等于商品售价及从购物到最后一次付款时的利息之和,即每期付款产生的本利和的累加与商品的付款总额相等,解决分期付款问题的数学方法就是等比数列求和.这也是等比数列在日常经济生活中的一个重要应用.思考辨析
判断下列说法是否正确,正确的在后面的括号内打“√”,错误的打“×”.
(1)银行储蓄中,本金与月利率均相同,存期1年,则使用复利计算应大于使用单利计算所得的本利和. ( )
(2)某产品计划每年成本降低m%,若三年后成本为a元,则现在成本是a(1+m%)3. ( )
(3)某工厂生产总值连续两年的年平均增长率依次为p%,q%,则这两年的平均增长率是 .( )
答案:(1)√ (2)× (3)√探究一探究二探究三规范解答
【例1】 某产品按质量分10个档次,生产最低档次的产品的利润是8元/件,每提高一个档次,利润每件增加2元,同时每提高一个档次,产量减少3件,在相同的时间内,最低档次的产品可生产60件.试问:在相同的时间内,应选择生产第几档次的产品可获得最大利润?(设最低档次为第1档次)
分析:由于总利润=第n档次的件数×第n档次每件的利润,因此需要求出第n档次的件数及第n档次的利润的表达式.探究一探究二探究三规范解答解:设在相同的时间内,从低到高每档次产品生产的件数分别为a1,a2,…,a10(单位:件),对应每档次产品的利润分别为b1,b2,…,b10(单位:元),则{an},{bn}均为等差数列,且a1=60,d=-3,b1=8,d'=2,
∴an=60-3(n-1)=-3n+63,
bn=8+2(n-1)=2n+6,
∴利润f(n)=anbn=(-3n+63)(2n+6)
=-6n2+108n+378=-6(n-9)2+864.
显然,当n=9时,f(n)max=f(9)=864元.
答:在相同的时间内,生产第9档次的产品可以获得最大利润.探究一探究二探究三规范解答反思感悟1.在实际问题中,若变化量在每次增加(或减少)的过程中不重复计算,增加(或减少)的量相同,且与正整数有关,则可以建立等差数列模型解决问题.
2.建立等差数列模型后,可以根据等差数列的通项公式an=a1+(n-1)d=am+(n-m)d与前n项和公式探究一探究二探究三规范解答 变式训练1 教育储蓄是一种零存整取的定期储蓄存款方式,它享受整存整取利率,利息免税.教育储蓄的对象为在校小学四年级(含四年级)以上的学生.假设零存整取3年期教育储蓄的月利率为2.325‰.按规定,3年期教育储蓄的存款总额不得超过2万元.?
(1)欲在3年后一次性支取本利和2万元,每月大约需存入多少元?
(2)零存整取3年期教育储蓄每月至多存入多少元?此时3年后本利和约为多少?(精确到1元)探究一探究二探究三规范解答解:(1)设每月存入A元,则有A(1+2.325‰)+A(1+2×2.325‰)+
…+A(1+36×2.325‰)=20 000.探究一探究二探究三规范解答(1)设n年内(本年度为第1年)总投入为an万元,旅游业总收入为bn万元,写出an,bn的表达式.
(2)至少经过几年旅游业的总收入将超过6 400万元?
分析: (1)从题意出发,从条件中提取有用的信息, 构造出等比数列,可用等比数列的前n项和公式求解. (2)令bn>6 400,解不等式即可.探究一探究二探究三规范解答探究一探究二探究三规范解答探究一探究二探究三规范解答反思感悟1.在实际问题中,若变化量每次增加(或减少)的百分数相同,且与正整数有关,则可以建立等比数列模型解决问题.
2.建立等比数列模型后,可利用等比数列的通项公式an=a1qn-1=amqn-m,前n项和公式探究一探究二探究三规范解答变式训练2某厂去年产值为a,计划在5年内每年比上一年产值增长10%,从今年起五年内这个工厂的总产值是( )
A.1.14 a B.1.15 a
C.10(1.15-1)a D.11(1.15-1)a
解析:由题意知,从今年起,这个工厂每年的产值构成以1.1a为首项,1.1为公比的等比数列.
答案:D探究一探究二探究三规范解答
【例3】小张老师年初向银行贷款2万元用于买车,银行贷款的年利率为10%,按复利计算.若这笔贷款要分10年等额还清,每年年初还一次,并且从借款后次年年初开始归还,问每年应还多少元?(精确到1元)
分析:从以下两点考虑:(1)每年按复利计算,即本年利息计入次年的本金生息;(2)分期付款,各期所付的款以及到最后一次付款时所生的利息合计,应等于2万元及2万元到最后一次付款时所生的利息之和.探究一探究二探究三规范解答解:设每年还款x元,需10年还清,则每年还款及利息情况如下:
第10年还款x元,此次欠款全部还清;
第9年还款x元,过1年欠款全部还清时,所付款连同利息之和为x(1+10%)元;
第8年还款x元,过2年欠款全部还清时,所付款连同利息之和为x(1+10%)2元;
……
第1年还款x元,过9年欠款全部还清时,所付款连同利息之和为x(1+10%)9元.
根据题意可得:
x+x(1+10%)+x(1+10%)2+…+x(1+10%)9=20 000(1+10%)10,∴每年应还款3 255元. 探究一探究二探究三规范解答反思感悟分期付款的相关规定:(1)分期付款中,每期的利息均按复利计算,分期付款中规定每期所付款额相同;(2)各期所付款额连同到最后一次付款时所产生的利息之和等于商品售价及从购买到最后一次付款时的利息之和(此为列方程的依据);(3)每期付款增值后的款数及售价增值后的款数均按S=P(1+r)n来计算,其中P代表本金(可以是每期付款额x,也可以是商品售价),n代表存期(月数或年数),r代表利率,S代表本利和.探究一探究二探究三规范解答变式训练3 某百货公司采用分期付款的办法销售家用空调机,售价为15 000元,分6个月付清,每月付一次,月利率以6%的单利计算,问购买者每月应付 元(不满1元的舍去).?
解析:设每月应付款为x元,则自第一月至付清本利合计为
x(1+0.06×5)+x(1+0.06×4)+…+x(1+0.06×1)+x
=x[6+0.06×(5+4+3+2+1)]=6.9x.
另一方面,15 000元在5个月的本利合计为
15 000(1+0.06×5)=19 500,6.9x=19 500,即x≈2 826(元).
答案:2 826探究一探究二探究三规范解答递推数列模型在实际中的应用
【典例】某地区位于沙漠边缘地区,人与沙漠进行长期不懈的斗争,到2014年底全地区的绿化率已达到30%,从2015年开始,每年将出现以下变化:原有沙漠面积的16%将栽上树,改造为绿洲,同时,原有绿洲面积的4%又被侵蚀,变为沙漠.分析:本题可以先建立递推数列关系,然后构造成所证明的数列结构,再间接求出an,进而求出所需年数.探究一探究二探究三规范解答探究一探究二探究三规范解答探究一探究二探究三规范解答反思提升如果某一个量,每一期以一个固定的百分数增加(或减少),或以一个固定的具体量增加(或减少)时,我们称这样的模型为生长模型,如分期付款、森林生长与砍伐、沙漠治理等问题就属于生长模型.探究一探究二探究三规范解答变式训练 一牧羊人赶着一群羊通过36个关口,每过一个关口,守关口人将拿走当时羊的一半,然后退还一只,过完这些关口后,牧羊人只剩下2只羊,问原来牧羊人赶了多少只羊??
解:设过第n关后牧羊人剩下an+1只羊,第n关前的羊数为an只,即2an+1=an+2(n=1,2,3,…).
由递推关系式得an=2(an+1-1),
将a36=2代入上式可得a35=a34=…=a1=2,
则a1即为牧羊人原来羊的只数2只.123451.有一套丛书共6册,计划2016年出版第一册,每两年出版一册,则出版齐这套丛书的年份是( )
A.2024 B.2026 C.2028 D.2029
解析:由已知得出版齐这套丛书的年份是2016+(6-1)×2=2026.
答案:B123452.某种细胞开始有2个,1小时后分裂成4个,2小时后分裂成8个,3小时后分裂成16个,……,按此规律,6小时后细胞的个数是( )
A.63 B.64 C.127 D.128
解析:细胞分裂的个数依次构成等比数列,
记为{an},则a1=2,公比q=2,
则a7=a1·q6=2×26=128.
答案:D123453.某种产品平均每三年价格降低 ,目前售价640元,则9年后此产品的价格为 元.?
解析:由题意知9年后的价格为
答案:270123454.夏季高山上气温从山脚起每升高100米降低约0.7 ℃,已知山顶气温是14.1 ℃,山脚的气温是26 ℃,则山顶相对于山脚的高度约是 米.?
解析:山顶气温与山脚气温相差26 ℃-14.1 ℃=11.9 ℃.
∵气温每升高100米降低约0.7 ℃,
∴山顶相对于山脚的高度约为
答案:1 700 123455.某渔场养鱼,第一年鱼的质量增长200%,以后每年的质量增长率是前一年增长率的一半.
(1)当饲养4年后,鱼的质量是原来的多少倍?
(2)如果由于某种原因,每年损失预计质量的10%,那么经过多少年后鱼的总质量开始减少?
解:(1)设鱼原来的质量为a,n年后鱼的质量为an,则
a1=(1+2)a=3a,a2=3a(1+1)=6a,
