高中数学北师大版必修五课件 第一章 数列习题课1 数列的综合应用 :43张PPT
文档属性
| 名称 | 高中数学北师大版必修五课件 第一章 数列习题课1 数列的综合应用 :43张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:36:35 | ||
图片预览








文档简介
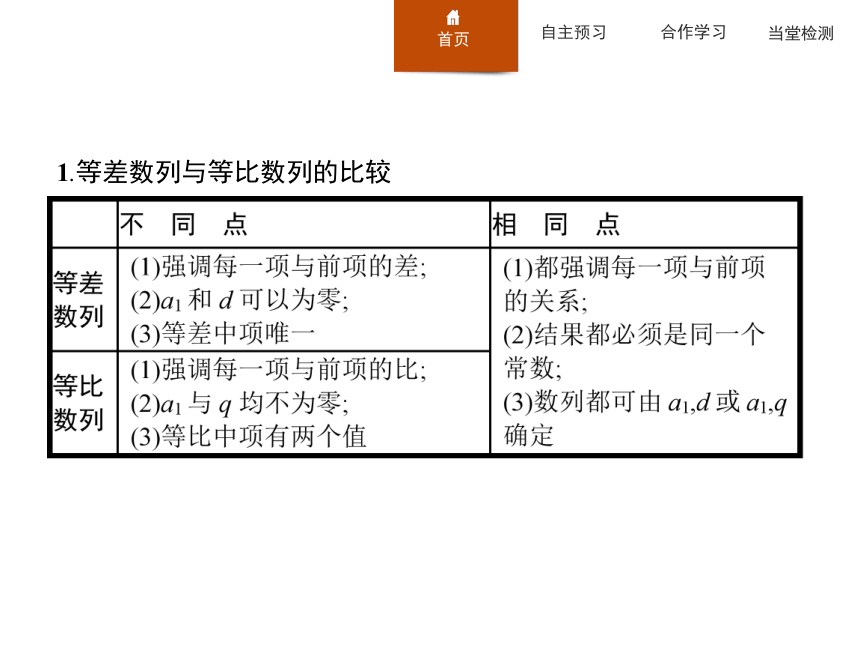
课件43张PPT。习题课 数列的综合应用1.等差数列与等比数列的比较 2.等差数列的常用性质
(1)通项公式的推广:an=am+(n-m)d(n,m∈N+).
(2)若{an}为等差数列,且k+l=m+n(k,l,m,n∈N+),则ak+al=am+an.
(3)若{an}是等差数列,公差为d,则{a2n}是等差数列,公差为2d.
(4)若{an},{bn}是等差数列,则{pan+qbn}是等差数列.
(5)若{an}是等差数列,则ak,ak+m,ak+2m,…(k,m∈N+)组成公差为md的等差数列.
(6)Sn,S2n-Sn,S3n-S2n组成新的等差数列.3.等比数列的常用性质
(1)在等比数列中,若m+n=p+q,则am·an=ap·aq(m,n,p,q∈N+).
(2)间隔相同的项,如a1,a3,a5,…仍为等比数列,且公比为q2.
(3)等比数列{an}的前n项和为Sn(Sn≠0),则Sn,S2n-Sn,S3n-S2n成等比数列,公比为qn.
(4)单调性q=1?{an}为常数列,q<0?{an}为摆动数列. 4.数列求和常用方法
(1)公式法(2)裂项相消法
把数列的通项拆分为两项之差,使之在求和时产生前后相互抵消的项的求和方法.
(3)错位相减法
①适用的数列:{anbn},其中数列{an}是公差为d的等差数列,{bn}是公比为q≠1的等比数列.
②方法:设Sn=a1b1+a2b2+…+anbn①,
则qSn=a1b2+a2b3+…+an-1bn+anbn+1②,
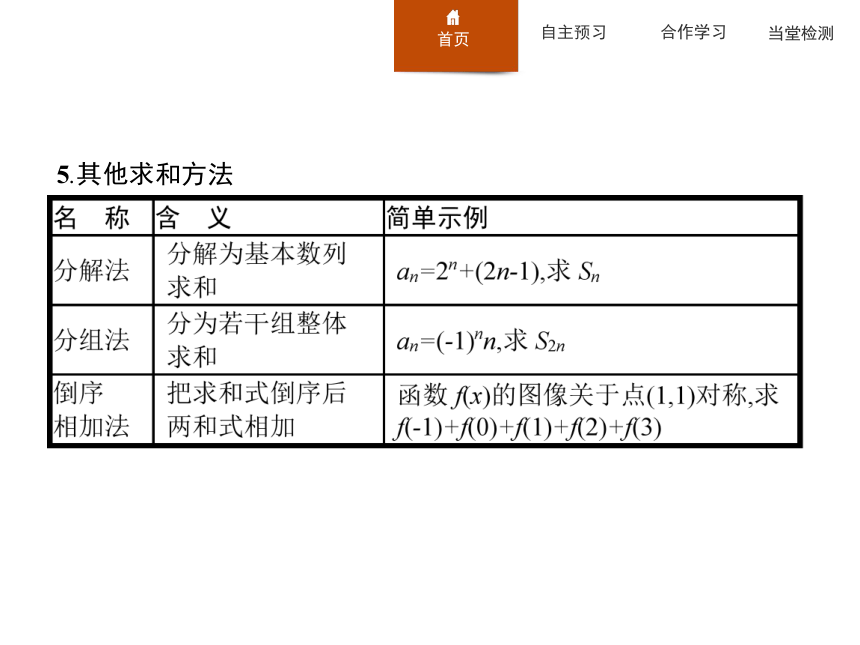
①-②得:(1-q)Sn=a1b1+d(b2+b3+…+bn)-anbn+1,就转化为根据公式可求的和.5.其他求和方法 【做一做1】设Sn为等差数列{an}的前n项和,若a3=3,S9-S6=27,则该数列的首项a1等于( )?答案:D
【做一做2】等比数列前n项和为Sn,有人算得S1=8,S2=20,S3=36,S4=65,后来发现有一个数算错了,错误的是( )?
A.S1 B.S2 C.S3 D.S4
答案:C
【做一做3】已知数列{an}满足a1=1, 则其前6项之和是( )?
A.16 B.20 C.33 D.120
答案:C【做一做4】数列{an}是首项a1=4的等比数列,且4a1,a5,-2a3成等差数列,则a2 017= .?
答案:4
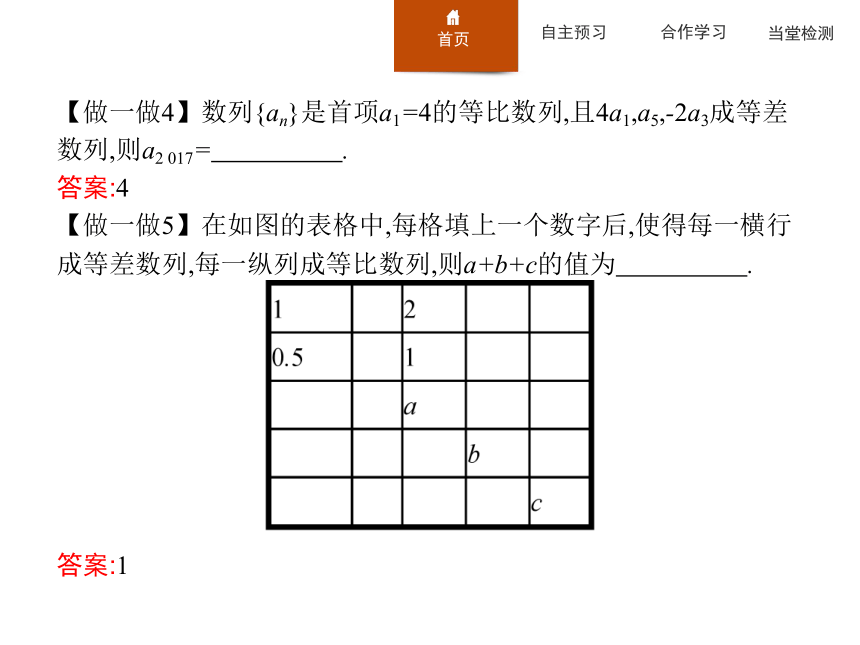
【做一做5】在如图的表格中,每格填上一个数字后,使得每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为 .?答案:1 探究一探究二探究三探究四探究五
【例1】 (1)已知等比数列{an}为递增数列.若a1>0,且2(an+an+2)=5an+1,则数列{an}的公比q= .?
(2)已知等差数列{an}的前5项和为105,且a10=2a5.
①求数列{an}的通项公式;
②对任意m∈N+,将数列{an}中不大于72m的项的个数记为bm,求数列{bm}的前m项和Sm.思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五反思感悟对于等差(等比)数列的基本运算要注意以下关键点:
(1)基本量.
在等差(比)数列中,首项a1和公差d(公比q)是两个基本量.
(2)解题思路.
①求公差d(公比q):常用公式an=am+(n-m)d(an=amqn-m);
②列方程组:当条件与结论的联系不明显时,常把条件转化为关于a1和d(q)的方程组求解,但要注意消元及整体计算,以减少计算量.思想方法探究一探究二探究三探究四探究五 变式训练1 已知等差数列{an}的公差d=1,前n项和为Sn.?
(1)若1,a1,a3成等比数列,求a1;
(2)若S5>a1a9,求a1的取值范围.
解:(1)因为数列{an}的公差d=1,且1,a1,a3成等比数列,思想方法探究一探究二探究三探究四探究五思想方法【例2】 (1)等差数列{an}中,如果a1+a4+a7=39,a3+a6+a9=27,那么数列{an}前9项的和为( )
A.297 B.144 C.99 D.66
A.9 B.1 C.2 D.3探究一探究二探究三探究四探究五思想方法答案:(1)C (2)D 探究一探究二探究三探究四探究五反思感悟 思想方法探究一探究二探究三探究四探究五变式训练2 (1)已知等差数列{an}的公差d=-2,
a1+a4+a7+…+a97=50,那么a3+a6+a9+…+a99的值是 ( )?
A.-78 B.-82 C.-148 D.-182
(2)在正项等比数列{an}中,a3a7=4,则数列{log2an}的前9项之和为 .?
解析:(2)由正项等比数列{an}中,a3a7=4,即得a5=2,
答案:(1)B (2)9思想方法探究一探究二探究三探究四探究五
【例3】 (1)已知数列{an}中,a1=1,an=2an-1+1(n≥2),则数列{an}的通项公式是 .?
(2)已知数列{an}与{bn}的前n项和分别为Sn,Tn,a1=1,b1=2,且对任意n∈N+,都有 ,Tn=2bn-2成立,求数列{an},{bn}的通项公式.(1)解析:由an=2an-1+1(n≥2)得an+1=2(an-1+1),即 ,所以数列{an+1}是首项为2,公比为2的等比数列,所以an+1=2n,所以an=2n-1.
答案:an=2n-1思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五反思感悟1.归纳猜想法:已知数列的前几项,求数列的通项公式,可采用归纳猜想法.
3.累加法:数列递推关系形如an+1=an+f(n),其中数列{f(n)}前n项和可求,这种类型的数列求通项公式时,常用累加法(叠加法).
4.累乘法:数列递推关系如an+1=g(n)an,其中数列{g(n)}前n项可求积,此数列求通项公式一般采用累乘法(叠乘法).思想方法探究一探究二探究三探究四探究五变式训练3 思想方法探究一探究二探究三探究四探究五【例4】 已知等差数列{an}的公差d≠0,它的前n项和为Sn,若S5=35,且a2,a7,a22成等比数列.
(1)求数列{an}的通项公式;
(2)设数列 的前n项和为Tn,求Tn.
分析:(1)列出关于首项a1和公差d的方程组即可;(2)利用裂项求和法求和.思想方法探究一探究二探究三探究四探究五解:(1)设数列的首项为a1.
因为S5=35,且a2,a7,a22成等比数列,思想方法探究一探究二探究三探究四探究五反思感悟1.数列求和应从通项入手,若无通项,则先求通项,然后通过对通项变形,转化为等差数列或等比数列或可求数列的前n项和的数列求和.
2.常用求和方法
有公式法、错位相减法、裂项相消法、并项求和法、分类求和法等.本例是典型的裂项相消法求和.思想方法探究一探究二探究三探究四探究五变式训练4 (2016山东高考)已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.?
(1)求数列{bn}的通项公式;
(2)令 ,求数列{cn}的前n项和Tn.
解:(1)由题意知当n≥2时,an=Sn-Sn-1=6n+5,
当n=1时,a1=S1=11,所以an=6n+5.
设数列{bn}的公差为d.思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五分析:(1)利用中点坐标公式得出x1+x2=1是关键;(2)利用倒序相加法求和;(3)利用裂项法求和.思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五反思感悟数列与函数的综合问题的题型及解题策略
(1)已知函数条件,解决数列问题,此类问题一般利用函数的性质、图像研究数列问题.
(2)已知数列条件,解决函数问题,解决此类问题一般要充分利用数列的范围、公式、求和方法对式子化简变形.另外,解题时要注意数列与函数的内在联系,灵活运用函数的思想方法求解,在问题的求解过程中往往会遇到递推数列,因此掌握递推数列的常见解法有助于该类问题的解决.思想方法探究一探究二探究三探究四探究五变式训练5 思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五思想方法函数与方程思想在数列中的应用
【典例】已知公差大于零的等差数列{an}的前n项和为Sn,且满足a2a4=65,a1+a5=18.
(1)若1(2)设 ,是否存在一个最小的常数m使得b1+b2+…+bn
分析:(1)本题的第一个切入点是利用等差数列性质求出a2和a4,进而求出{an}的通项公式;(2)本题的第二个切入点是先求Sn,进而确定bn.探究一探究二探究三探究四探究五思想方法 解:(1)数列{an}为等差数列,因为a1+a5=a2+a4=18,又a2a4=65,所以a2,a4是方程x2-18x+65=0的两个根,又公差d>0,所以a22.对于数列的求和,先要弄清数列的形式,然后再选用合理的方法,作为本题就是裂项求和法的应用.
3.对于不等式的恒成立问题还要有函数意识,对于第(2)问中m的求解,就需要将b1+b2+b3+…+bn看作关于n的函数来求解.探究一探究二探究三探究四探究五思想方法 变式训练 已知数列{an}的前n项和为Sn,a1=1,且3an+1+2Sn=3(n为正整数).?
(1)求a2,a3的值,并求数列{an}的通项公式;
(2)若对任意正整数n,k≤Sn恒成立,求实数k的最大值.探究一探究二探究三探究四探究五思想方法123451.已知Sn为数列{an}的前n项和,且满足2an-a1=S1·Sn(a1≠0,n∈N+),则a7等于( )
A.16 B.32 C.64 D.128
答案:C6123452.已知{an}为等比数列,Sn是它的前n项和.若a2·a3=2a1,且a4与2a7的等差中项为 ,则S5等于( )
A.35 B.33
C.31 D.29
答案:C6123453.设数列{an},{bn}都是等差数列.若a1+b1=7,a3+b3=21,则a5+b5= .?
解析:∵(a1+a5)+(b1+b5)=2(a3+b3)=42,∴a5+b5=42-7=35.
答案:356123454.已知数列{an}的前n项和为Sn,且Sn=2n-an,则数列{an}的通项公式an= .?6123455.已知数列{an}是3+2-1,6+22-1,9+23-1,12+24-1,…,写出数列{an}的通项公式并求其前n项和Sn.
解:由已知得,数列{an}的通项公式为an=3n+2n-1=3n-1+2n,
∴Sn=a1+a2+…+an61234566.已知函数f(x)=logmx(m为常数,0解:由题意f(an)=2+(n-1)×2=2n,即logman=2n,
所以an=m2n,bn=an·f(an)=2n·m2n,
(1)通项公式的推广:an=am+(n-m)d(n,m∈N+).
(2)若{an}为等差数列,且k+l=m+n(k,l,m,n∈N+),则ak+al=am+an.
(3)若{an}是等差数列,公差为d,则{a2n}是等差数列,公差为2d.
(4)若{an},{bn}是等差数列,则{pan+qbn}是等差数列.
(5)若{an}是等差数列,则ak,ak+m,ak+2m,…(k,m∈N+)组成公差为md的等差数列.
(6)Sn,S2n-Sn,S3n-S2n组成新的等差数列.3.等比数列的常用性质
(1)在等比数列中,若m+n=p+q,则am·an=ap·aq(m,n,p,q∈N+).
(2)间隔相同的项,如a1,a3,a5,…仍为等比数列,且公比为q2.
(3)等比数列{an}的前n项和为Sn(Sn≠0),则Sn,S2n-Sn,S3n-S2n成等比数列,公比为qn.
(4)单调性q=1?{an}为常数列,q<0?{an}为摆动数列. 4.数列求和常用方法
(1)公式法(2)裂项相消法
把数列的通项拆分为两项之差,使之在求和时产生前后相互抵消的项的求和方法.
(3)错位相减法
①适用的数列:{anbn},其中数列{an}是公差为d的等差数列,{bn}是公比为q≠1的等比数列.
②方法:设Sn=a1b1+a2b2+…+anbn①,
则qSn=a1b2+a2b3+…+an-1bn+anbn+1②,
①-②得:(1-q)Sn=a1b1+d(b2+b3+…+bn)-anbn+1,就转化为根据公式可求的和.5.其他求和方法 【做一做1】设Sn为等差数列{an}的前n项和,若a3=3,S9-S6=27,则该数列的首项a1等于( )?答案:D
【做一做2】等比数列前n项和为Sn,有人算得S1=8,S2=20,S3=36,S4=65,后来发现有一个数算错了,错误的是( )?
A.S1 B.S2 C.S3 D.S4
答案:C
【做一做3】已知数列{an}满足a1=1, 则其前6项之和是( )?
A.16 B.20 C.33 D.120
答案:C【做一做4】数列{an}是首项a1=4的等比数列,且4a1,a5,-2a3成等差数列,则a2 017= .?
答案:4
【做一做5】在如图的表格中,每格填上一个数字后,使得每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为 .?答案:1 探究一探究二探究三探究四探究五
【例1】 (1)已知等比数列{an}为递增数列.若a1>0,且2(an+an+2)=5an+1,则数列{an}的公比q= .?
(2)已知等差数列{an}的前5项和为105,且a10=2a5.
①求数列{an}的通项公式;
②对任意m∈N+,将数列{an}中不大于72m的项的个数记为bm,求数列{bm}的前m项和Sm.思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五反思感悟对于等差(等比)数列的基本运算要注意以下关键点:
(1)基本量.
在等差(比)数列中,首项a1和公差d(公比q)是两个基本量.
(2)解题思路.
①求公差d(公比q):常用公式an=am+(n-m)d(an=amqn-m);
②列方程组:当条件与结论的联系不明显时,常把条件转化为关于a1和d(q)的方程组求解,但要注意消元及整体计算,以减少计算量.思想方法探究一探究二探究三探究四探究五 变式训练1 已知等差数列{an}的公差d=1,前n项和为Sn.?
(1)若1,a1,a3成等比数列,求a1;
(2)若S5>a1a9,求a1的取值范围.
解:(1)因为数列{an}的公差d=1,且1,a1,a3成等比数列,思想方法探究一探究二探究三探究四探究五思想方法【例2】 (1)等差数列{an}中,如果a1+a4+a7=39,a3+a6+a9=27,那么数列{an}前9项的和为( )
A.297 B.144 C.99 D.66
A.9 B.1 C.2 D.3探究一探究二探究三探究四探究五思想方法答案:(1)C (2)D 探究一探究二探究三探究四探究五反思感悟 思想方法探究一探究二探究三探究四探究五变式训练2 (1)已知等差数列{an}的公差d=-2,
a1+a4+a7+…+a97=50,那么a3+a6+a9+…+a99的值是 ( )?
A.-78 B.-82 C.-148 D.-182
(2)在正项等比数列{an}中,a3a7=4,则数列{log2an}的前9项之和为 .?
解析:(2)由正项等比数列{an}中,a3a7=4,即得a5=2,
答案:(1)B (2)9思想方法探究一探究二探究三探究四探究五
【例3】 (1)已知数列{an}中,a1=1,an=2an-1+1(n≥2),则数列{an}的通项公式是 .?
(2)已知数列{an}与{bn}的前n项和分别为Sn,Tn,a1=1,b1=2,且对任意n∈N+,都有 ,Tn=2bn-2成立,求数列{an},{bn}的通项公式.(1)解析:由an=2an-1+1(n≥2)得an+1=2(an-1+1),即 ,所以数列{an+1}是首项为2,公比为2的等比数列,所以an+1=2n,所以an=2n-1.
答案:an=2n-1思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五反思感悟1.归纳猜想法:已知数列的前几项,求数列的通项公式,可采用归纳猜想法.
3.累加法:数列递推关系形如an+1=an+f(n),其中数列{f(n)}前n项和可求,这种类型的数列求通项公式时,常用累加法(叠加法).
4.累乘法:数列递推关系如an+1=g(n)an,其中数列{g(n)}前n项可求积,此数列求通项公式一般采用累乘法(叠乘法).思想方法探究一探究二探究三探究四探究五变式训练3 思想方法探究一探究二探究三探究四探究五【例4】 已知等差数列{an}的公差d≠0,它的前n项和为Sn,若S5=35,且a2,a7,a22成等比数列.
(1)求数列{an}的通项公式;
(2)设数列 的前n项和为Tn,求Tn.
分析:(1)列出关于首项a1和公差d的方程组即可;(2)利用裂项求和法求和.思想方法探究一探究二探究三探究四探究五解:(1)设数列的首项为a1.
因为S5=35,且a2,a7,a22成等比数列,思想方法探究一探究二探究三探究四探究五反思感悟1.数列求和应从通项入手,若无通项,则先求通项,然后通过对通项变形,转化为等差数列或等比数列或可求数列的前n项和的数列求和.
2.常用求和方法
有公式法、错位相减法、裂项相消法、并项求和法、分类求和法等.本例是典型的裂项相消法求和.思想方法探究一探究二探究三探究四探究五变式训练4 (2016山东高考)已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.?
(1)求数列{bn}的通项公式;
(2)令 ,求数列{cn}的前n项和Tn.
解:(1)由题意知当n≥2时,an=Sn-Sn-1=6n+5,
当n=1时,a1=S1=11,所以an=6n+5.
设数列{bn}的公差为d.思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五分析:(1)利用中点坐标公式得出x1+x2=1是关键;(2)利用倒序相加法求和;(3)利用裂项法求和.思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五反思感悟数列与函数的综合问题的题型及解题策略
(1)已知函数条件,解决数列问题,此类问题一般利用函数的性质、图像研究数列问题.
(2)已知数列条件,解决函数问题,解决此类问题一般要充分利用数列的范围、公式、求和方法对式子化简变形.另外,解题时要注意数列与函数的内在联系,灵活运用函数的思想方法求解,在问题的求解过程中往往会遇到递推数列,因此掌握递推数列的常见解法有助于该类问题的解决.思想方法探究一探究二探究三探究四探究五变式训练5 思想方法探究一探究二探究三探究四探究五思想方法探究一探究二探究三探究四探究五思想方法函数与方程思想在数列中的应用
【典例】已知公差大于零的等差数列{an}的前n项和为Sn,且满足a2a4=65,a1+a5=18.
(1)若1
3.对于不等式的恒成立问题还要有函数意识,对于第(2)问中m的求解,就需要将b1+b2+b3+…+bn看作关于n的函数来求解.探究一探究二探究三探究四探究五思想方法 变式训练 已知数列{an}的前n项和为Sn,a1=1,且3an+1+2Sn=3(n为正整数).?
(1)求a2,a3的值,并求数列{an}的通项公式;
(2)若对任意正整数n,k≤Sn恒成立,求实数k的最大值.探究一探究二探究三探究四探究五思想方法123451.已知Sn为数列{an}的前n项和,且满足2an-a1=S1·Sn(a1≠0,n∈N+),则a7等于( )
A.16 B.32 C.64 D.128
答案:C6123452.已知{an}为等比数列,Sn是它的前n项和.若a2·a3=2a1,且a4与2a7的等差中项为 ,则S5等于( )
A.35 B.33
C.31 D.29
答案:C6123453.设数列{an},{bn}都是等差数列.若a1+b1=7,a3+b3=21,则a5+b5= .?
解析:∵(a1+a5)+(b1+b5)=2(a3+b3)=42,∴a5+b5=42-7=35.
答案:356123454.已知数列{an}的前n项和为Sn,且Sn=2n-an,则数列{an}的通项公式an= .?6123455.已知数列{an}是3+2-1,6+22-1,9+23-1,12+24-1,…,写出数列{an}的通项公式并求其前n项和Sn.
解:由已知得,数列{an}的通项公式为an=3n+2n-1=3n-1+2n,
∴Sn=a1+a2+…+an61234566.已知函数f(x)=logmx(m为常数,0
所以an=m2n,bn=an·f(an)=2n·m2n,
