人教版六上第5单元第3课时《圆的面积》同步练习(含答案及解析)
文档属性
| 名称 | 人教版六上第5单元第3课时《圆的面积》同步练习(含答案及解析) |  | |
| 格式 | zip | ||
| 文件大小 | 81.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-24 20:56:49 | ||
图片预览



文档简介
第5单元第3课时《圆的面积》同步练习
一、单选题。
1、圆的面积与它的( )无关。
A、圆心 B、半径 C、周长
2、直径2分米的圆,它的面积是( )
A.31.4平方分米 B.314平方厘米 C.12.56平方分米 D.3.14平方厘米
3、半径是2厘米的圆,它的周长和面积相比( )
A.周长大 B.面积大 C.周长和面积相等 D.无法比较
4、大小两个圆的半径之比是3:1,则它们的面积之比是( )
A.3:1 B.6:1 C.9:1 D.9:2
5、一个圆的半径扩大3倍,面积扩大( )倍.
A、3 B、6 C、9
6、一个环形内圆半径为14厘米,外圆半径为18厘米,环形面积是( )
A.128π B.64π C.196π D.32π
7、挂钟的时针长9厘米,一昼夜这根时针走过的面积是多少平方厘米?正确列式是( ).
A、9×2×3.14 B、3.14×92×2 C、3.14×92
8、大圆半径是小圆的直径,小圆面积与大圆面积之比是( ).
A、1:2 B、2:1 C、1:4 D、3:5
9、一个圆形水池周长是31.4米,在它周围修一条1米宽的水泥路,水泥路面积是( )平方米.
A.34.54 B.65.94 C.3.14
10、周长为800m的正方形铁片,要在其上截出一个圆,该圆最大面积是( ).
A、100π平方米 B、1000π平方米 C、10000π平方米 D、100000π平方米
二、填空题。
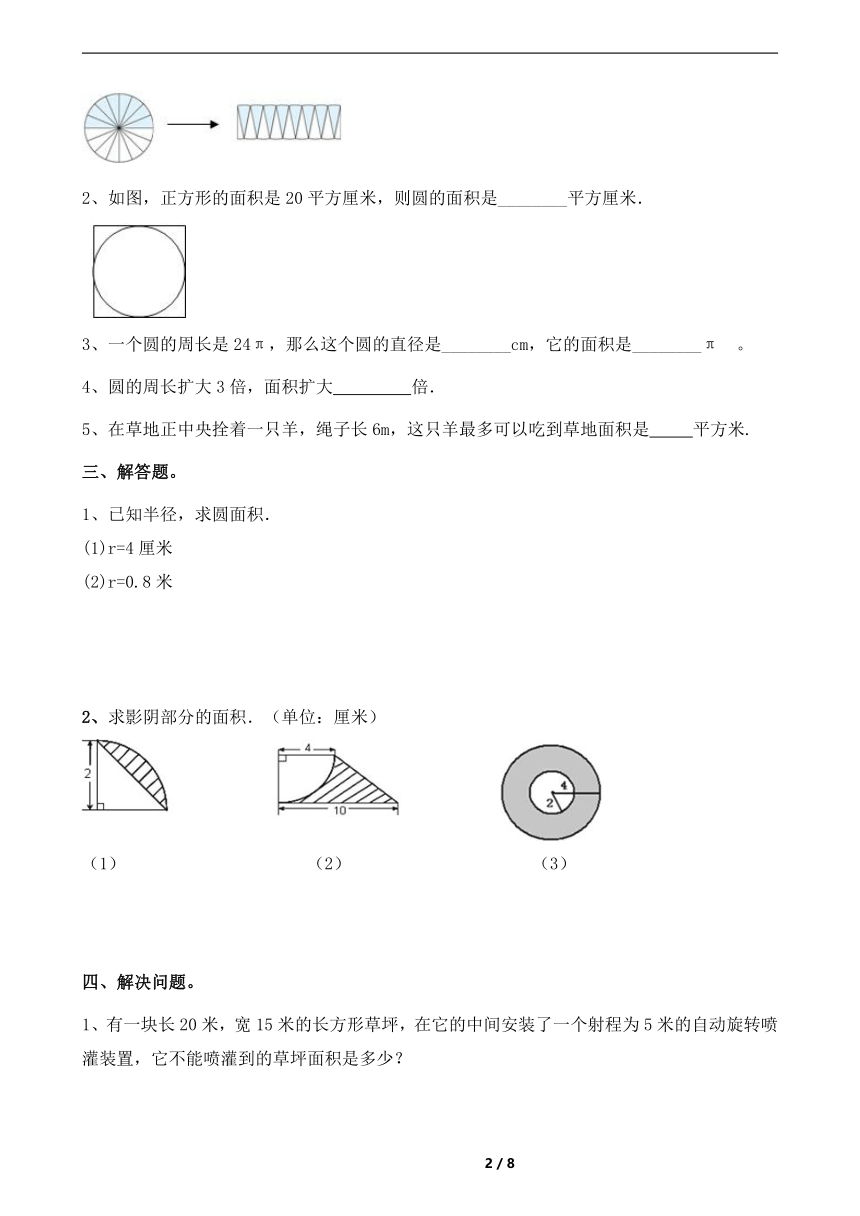
1、将一个圆形纸片剪成16等份,将每份剪下后拼接成一个近似的长方形,已知长方形的长为6.28cm,这个圆形纸片的面积是 平方厘米.
2、如图,正方形的面积是20平方厘米,则圆的面积是________平方厘米.
3、一个圆的周长是24π,那么这个圆的直径是________cm,它的面积是________π 。
4、圆的周长扩大3倍,面积扩大 倍.
5、在草地正中央拴着一只羊,绳子长6m,这只羊最多可以吃到草地面积是 平方米.
三、解答题。
1、已知半径,求圆面积.
(1)r=4厘米
(2)r=0.8米
2、求影阴部分的面积.(单位:厘米)
(1) (2) (3)
四、解决问题。
1、有一块长20米,宽15米的长方形草坪,在它的中间安装了一个射程为5米的自动旋转喷灌装置,它不能喷灌到的草坪面积是多少?
2、如图,运动场的两侧是两个半圆,它们的面积和是100π,中间的长方形的长是宽的1.5倍。
(1)求运动场的周长;
(2)求运动场的面积。
3、下图池塘的周长251.2米,池塘周围(阴影)是一条5米宽的水泥路,在路的外侧围一圈栏杆。水泥路的面积是多少?栏杆长多少米?
参考答案
一、单选题。
1、
【答案】A
【解析】根据圆的面积公式S=π ,圆的面积与圆的半径有关,又因为d=2r、C=2πr所以圆的面积与它的直径和周长也有关系,圆心只能确定圆的位置,而不能确定圆的大小。
2、
【答案】B
【解析】先求出圆的半径:2÷2=1(分米),然后根据圆的面积公式:S=πr2,代入数据答案即可.2÷2=1(分米)
圆的面积为:
3.14×12
=3.14(平方分米)
=314(平方厘米)
3、
【答案】D
【解析】圆的周长是指围成圆一周的长度,面积则是指圆的大小,周长用长度单位,面积用面积单位,它们不能比较大小.
4、
【答案】C
【解析】设小圆的半径为r,则大圆的半径为3r,代入圆的面积公式,表示出各自的面积,作比、化简即可求解.
5、
【答案】C
【解析】依据圆的面积公式即可.若r扩大3倍,则其面积扩大=9倍.
6、
【答案】A
【解析】根据圆环的面积公式:圆环的面积=π(R2﹣r2),计算即可求解.
7、
【答案】B
【解析】首先要明确的是,经过一昼夜,时针围绕钟面转了两周,而转一周所走过的面积是以针的长度为半径的圆的面积,利用圆的面积S=πr2即可求解.此题主要考查圆的面积的计算方法,关键是明白:时针的长度就是圆的半径.
3.14×92×2,
=3.14×81×2,
=508.68(平方厘米)
8、
【答案】C
【解析】 设小圆的半径为r,则大圆的半径2r; 则小圆面积:大圆面积=
πr?:π(2r)?=1:4.
9、
【答案】A
【解析】根据环形面积=外圆面积﹣内圆面积,首先根据圆的周长公式:c=2πr,已知圆形水池的周长是31.4米,求出水池的半径,水池的半径加上1米就是外圆的半径,把数据代入环形面积公式S=π(R2﹣r2)答案即可.
10、
【答案】C
【解析】在正方形内剪最大的圆时,则圆的直径与正方形的边长相等,所以用正方形的周长除以4即可求出圆的直径,进而求出它的半径,最后再根据圆的面积计算公式进行解答即可。
800÷4=200(米) 200÷2=100(米) 100×100×π=10000π(平方米)
二、填空题。
1、
【答案】12.56
【解析】由题意可得:长方形的长等于圆的周长的一半,宽等于圆的半径,长方形的长已知,于是即可求出圆的周长,进而得出圆的半径,得出圆的面积.
6.28÷3.14=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)
2、
【答案】15.7
【解析】这个最大圆的直径应该等于正方形的边长,正方形的面积已知,从而可以求出半径的平方值,进而可以求出圆的面积.
3.14×(20÷4),
=3.14×5,
=15.7(平方厘米).
答:圆的面积是15.7平方厘米.
3、
【答案】24,144
【解析】要求圆的直径时,直接用圆的周长除以圆周率即可,用求出的圆的直径除以2即可求出圆的半径,然后再根据圆的面积计算公式进行解答即可。
24π÷π=24(cm)
24÷2=12(cm)
12×12×π=144π(cm?)
4、
【答案】9
【解析】根据圆的周长公式可知:圆的周长与半径成正比例:圆的周长扩大3倍,则圆的半径就是扩大了3倍;
根据圆的面积公式可得:圆的面积与圆的半径的平方成正比例,半径扩大了3倍,则圆的面积就扩大了3?倍,即9倍.
5、
【答案】113.04
【解析】羊能吃到草的面积,就是以6米为半径的圆的面积,由此利用圆的面积公式S=πr2即可答案.
3.14×62
=3.14×36
=113.04(平方米)
三、解答题。
1、
【答案】(1)50.24平方厘米
(2)2.0096平方米
【解析】圆的周长=圆周率×直径=圆周率×半径×2;圆的面积=圆周率×半径×半径.
2、
【答案】① ×3.14×22﹣2×2÷2
=3.14﹣2
=1.14(平方厘米);
②(4+10)×4÷2﹣ ×3.14×42
=14×4÷2﹣3.14×4
=28﹣12.56
=15.44(平方厘米);
③3.14×(42﹣22)
=3.14×12
=37.68(平方厘米)
【解析】①阴影部分的面积就等于半径为2厘米的 圆的面积减去直角边为2厘米的等腰直角三角形的面积,据此解答即可;②阴影部分的面积就等于梯形的面积减去半径为4厘米的 圆的面积,据此解答即可;③利用圆环的面积公式S=π(R2﹣r2),代入数据即可求解.解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求解.
四、解决问题。
1、
【答案】20×15-3.14×5?=300-78.5=221.5(平方米)
2、
【答案】(1)周长:100π÷π=100(平方米),100=10×10,直径为:10×2=20(米),长:20×1.5=30(米)
20π+30×2
=20π+60(米)
(2)面积:10×10×π+30×20
=100π+600(平方米)
故答案为:20π+60,600+100π。
【解析】(1)用弯道的面积除以圆周率即可求出半径的平方,进而求出圆的半径,根据圆的周长计算公式求出弯道的长度,再加上中间直道长方形的两条长即可;(2)要求它的面积时,则直接用弯道的面积加上中间长方形的面积即可。
3、
【答案】(1)251.2÷3.14÷2=40(米)
水泥路面积=3.14×(40+5)?-3.14×40?=1334.5(平方米)
(2)3.14×2×(40+5)=282.6(米)
【解析】(1)求水泥路面积,就是求圆环的面积,用大圆面积减去小圆面积即可(2)求栏杆的长度,就是求大圆的周长,根据周长公式计算即可。
1 / 8
