人教高中数学必修四 1.2.1任意角的三角函数 课件(21张ppt)
文档属性
| 名称 | 人教高中数学必修四 1.2.1任意角的三角函数 课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 476.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
1.2 任意角的三角函数
1.2.1 任意角的三角函数
温故而知新
1.1设α是一个任意角,它的终边与单位圆交于点P(x,y),角α的三角函数分别为
1.2
若点P(x,y)为角α终边上任意一点,那么sinα,cosα,tanα对应的函数值分别等于什么?
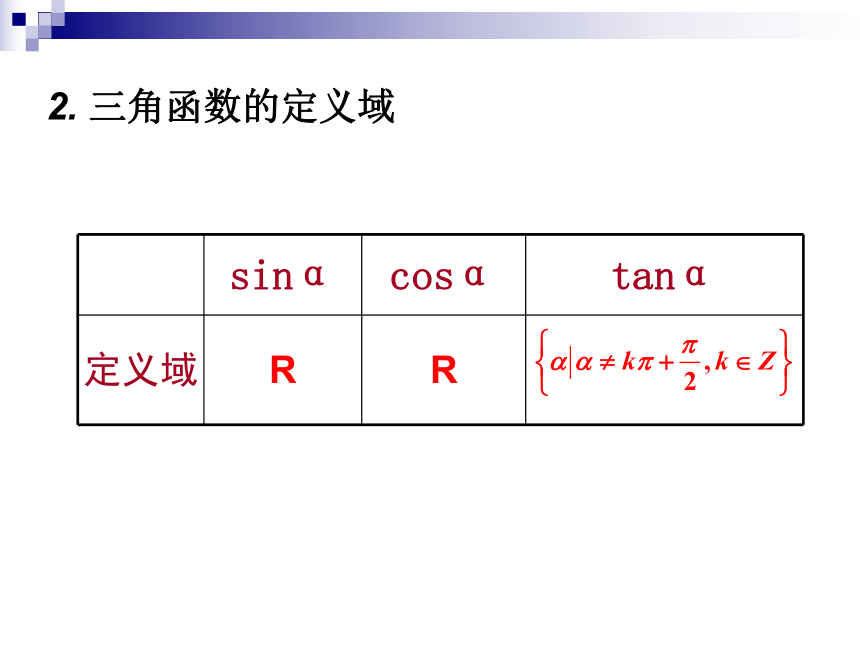
2. 三角函数的定义域
sinα cosα tanα
定义域 R R
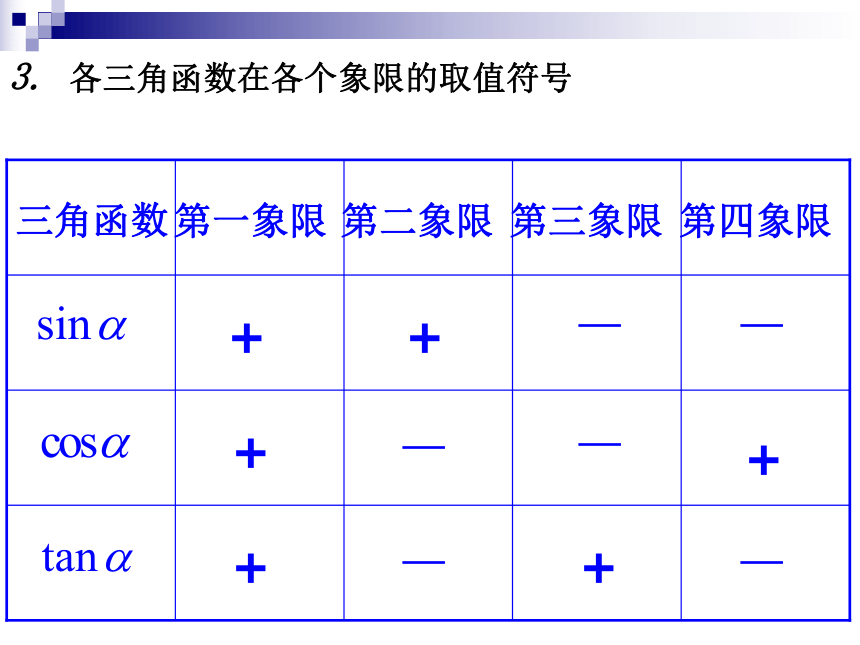
终边相同的角的同一三角函数值相等.
公式一:
知识探究(一):正弦线和余弦线
思考3:为了简化上述表示,我们设想将线段的两个端点规定一个为始点,另一个为终点,使得线段具有方向性,带有正负值符号.根据实际需要,应如何规定线段的正方向和负方向?
规定:线段从始点到终点与坐标轴同向时为正方向,反向时为负方向.
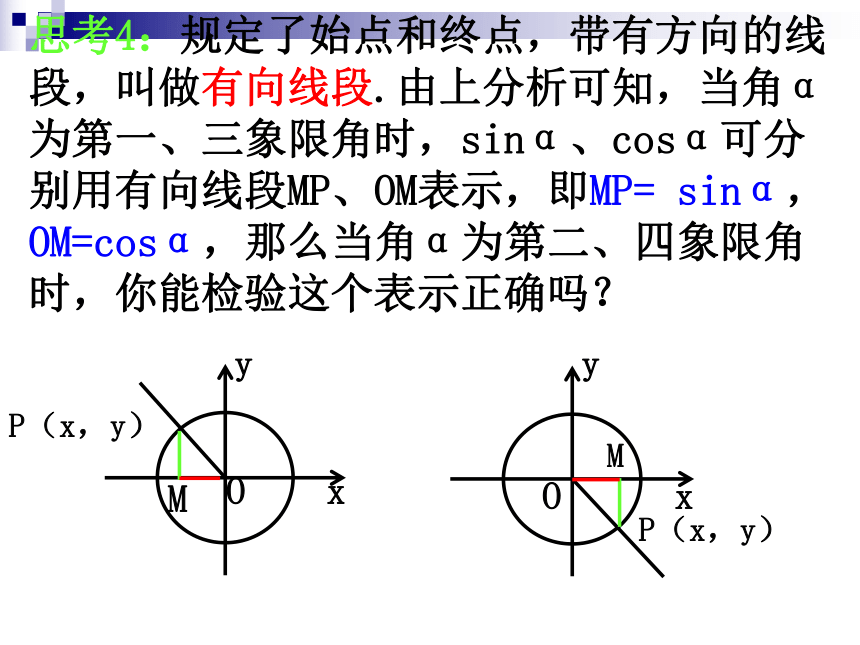
思考4:规定了始点和终点,带有方向的线段,叫做有向线段.由上分析可知,当角α为第一、三象限角时,sinα、cosα可分别用有向线段MP、OM表示,即MP= sinα,OM=cosα,那么当角α为第二、四象限角时,你能检验这个表示正确吗?
思考5:设角α的终边与单位圆的交点为P,过点P作x轴的垂线,垂足为M,称有向线段MP,OM分别为角α的正弦线和余弦线.当角α的终边在坐标轴上时,角α的正弦线和余弦线的含义如何?
思考6:设α为锐角,你能根据正弦线和余弦线说明sinα+cosα>1吗?
MP+OM>OP=1
知识探究(二):正切线
思考5:根据上述分析,你能描述正切线的几何特征吗?
过点A(1,0)作单位圆的切线,与角α的终边或其反向延长线相交于点T,则AT=tanα.
思考6:当角α的终边在坐标轴上时,角α的正切线的含义如何?
当角α的终边在x轴上时,角α的正切线是一个点;当角α的终边在y轴上时,角α的正切线不存在.
思考7:对于不等式
(其中α为锐角),你能用数形结合思想证明吗?
小结作业
1.三角函数线是三角函数的一种几何表示,即用有向线段表示三角函数值,是今后进一步研究三角函数图象的有效工具.
2.正弦线的始点随角的终边位置的变化而变化,余弦线和正切线的始点都是定点,分别是原点O和点A(1,0).
3.利用三角函数线处理三角不等式问题,是一种重要的方法和技巧,也是一种数形结合的数学思想.
1.2 任意角的三角函数
1.2.1 任意角的三角函数
温故而知新
1.1设α是一个任意角,它的终边与单位圆交于点P(x,y),角α的三角函数分别为
1.2
若点P(x,y)为角α终边上任意一点,那么sinα,cosα,tanα对应的函数值分别等于什么?
2. 三角函数的定义域
sinα cosα tanα
定义域 R R
终边相同的角的同一三角函数值相等.
公式一:
知识探究(一):正弦线和余弦线
思考3:为了简化上述表示,我们设想将线段的两个端点规定一个为始点,另一个为终点,使得线段具有方向性,带有正负值符号.根据实际需要,应如何规定线段的正方向和负方向?
规定:线段从始点到终点与坐标轴同向时为正方向,反向时为负方向.
思考4:规定了始点和终点,带有方向的线段,叫做有向线段.由上分析可知,当角α为第一、三象限角时,sinα、cosα可分别用有向线段MP、OM表示,即MP= sinα,OM=cosα,那么当角α为第二、四象限角时,你能检验这个表示正确吗?
思考5:设角α的终边与单位圆的交点为P,过点P作x轴的垂线,垂足为M,称有向线段MP,OM分别为角α的正弦线和余弦线.当角α的终边在坐标轴上时,角α的正弦线和余弦线的含义如何?
思考6:设α为锐角,你能根据正弦线和余弦线说明sinα+cosα>1吗?
MP+OM>OP=1
知识探究(二):正切线
思考5:根据上述分析,你能描述正切线的几何特征吗?
过点A(1,0)作单位圆的切线,与角α的终边或其反向延长线相交于点T,则AT=tanα.
思考6:当角α的终边在坐标轴上时,角α的正切线的含义如何?
当角α的终边在x轴上时,角α的正切线是一个点;当角α的终边在y轴上时,角α的正切线不存在.
思考7:对于不等式
(其中α为锐角),你能用数形结合思想证明吗?
小结作业
1.三角函数线是三角函数的一种几何表示,即用有向线段表示三角函数值,是今后进一步研究三角函数图象的有效工具.
2.正弦线的始点随角的终边位置的变化而变化,余弦线和正切线的始点都是定点,分别是原点O和点A(1,0).
3.利用三角函数线处理三角不等式问题,是一种重要的方法和技巧,也是一种数形结合的数学思想.
