2019_2020学年高中数学第二章基本初等函数(Ⅰ)2.2.2对数函数及其性质第一课时对数函数的图象及性质课件新人教A版必修1:39张PPT
文档属性
| 名称 | 2019_2020学年高中数学第二章基本初等函数(Ⅰ)2.2.2对数函数及其性质第一课时对数函数的图象及性质课件新人教A版必修1:39张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 719.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-23 12:52:18 | ||
图片预览










文档简介
课件39张PPT。2.2.2 对数函数及其性质
第一课时 对数函数的图象及性质[目标导航]新知导学·素养养成1.对数函数的概念
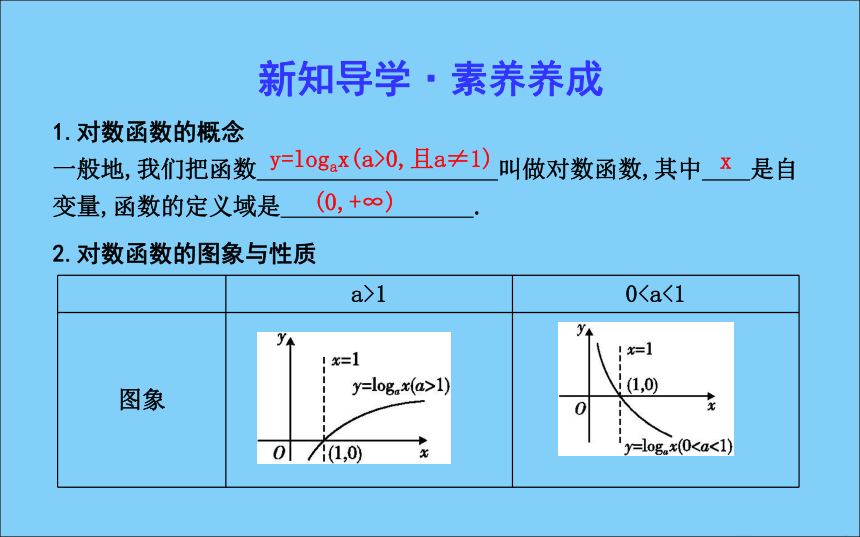
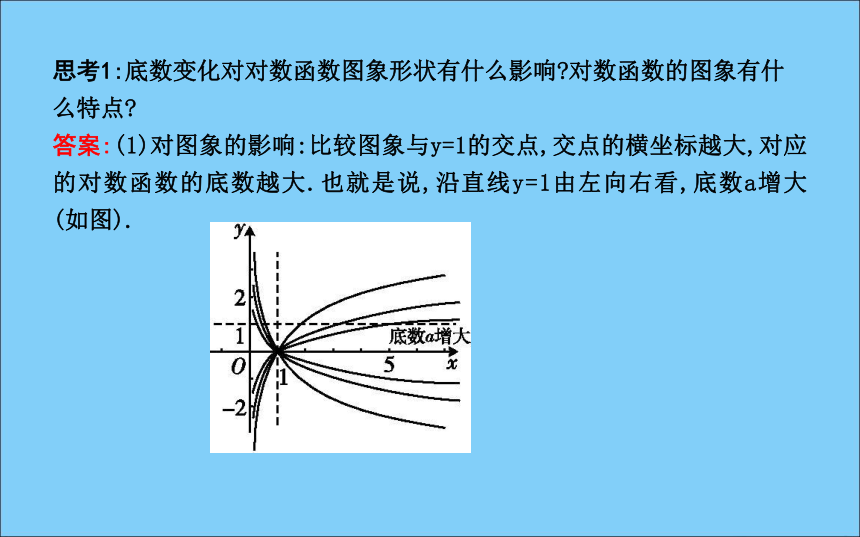
一般地,我们把函数 叫做对数函数,其中 是自变量,函数的定义域是 .y=logax(a>0,且a≠1)x(0,+∞) 2.对数函数的图象与性质(1,0)增减思考1:底数变化对对数函数图象形状有什么影响?对数函数的图象有什么特点?
答案:(1)对图象的影响:比较图象与y=1的交点,交点的横坐标越大,对应的对数函数的底数越大.也就是说,沿直线y=1由左向右看,底数a增大 (如图).3.反函数
对数函数y=logax(a>0,且a≠1)和指数函数y=ax(a>0,且a≠1)互为
.反函数思考2:同底数的指数、对数函数的定义域、值域有何关系?
答案:同底数的指数函数的定义域是同底数对数函数的值域,指数函数的值域是对数函数的定义域.
思考3:互为反函数的两个函数图象有何特征?
答案:关于直线y=x对称.名师点津(1)对数函数图象和性质的关系(2)若函数y=f(x)存在反函数,且点(a,b)在y=f(x)图象上,则点(b,a)必在其反函数图象上.课堂探究·素养提升题型一 对数函数的概念
[例1] (1)若函数y=log(2a-1)x+(a2-5a+4)是对数函数,则a= .答案:(1)4 答案:(2)2方法技巧(1)判断一个函数是对数函数必须是形如y=logax(a>0,且a≠1)的形式,即必须满足以下条件:
①系数为1;
②底数为大于0且不等于1的常数;
③对数的真数仅有自变量x.
(2)若已知对数函数过定点求解析式时,常用待定系数法,设f(x)= logax(a>0,且a≠1),将定点代入后利用指对数式互化或指数幂的运算性质求a.题型二 对数函数的图象特征
[例2] (1)已知函数y=loga(x+c)(a,c为常数,其中a>0,且a≠1)的图象如图,则下列结论成立的是( )
(A)a>0,c>1 (B)a>1,0(C)01 (D)0又x=0时,logac>0,即logac>loga1,
故01时,函数y=logax是增函数,C,D不正确;直线y=(1-a)x的斜率小于0,所以A不正确,B正确.故选B.即时训练2-1:(1)当a>1时,函数y=logax和y=(1-a)x的图象只可能是( )解析:(2)法一 若01,则函数y=ax的图象上升且过点(0,1),而函数y=loga(-x)的图象下降且过点(-1,0),只有B中图象符合.故选B.
法二 首先指数函数y=ax的图象只可能在上半平面,函数y=loga(-x)的图象只可能在左半平面,从而排除A,C;再看单调性,y=ax与y=loga (-x)的单调性正好相反,排除D.只有B中图象符合.故选B.(2)已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )方法技巧(1)y=ax与y=logax(a>0,且a≠1)互为反函数.
(2)若函数y=f(x)存在反函数,且y=f(x)过点(a,b),则其反函数过点(b,a).
(3)反函数的定义域是原函数的值域.[备用例3] 若函数f(x)=loga(x+b)+c(a>0,且a≠1)的反函数图象恒过定点(2,3),则b+c= .?解析:由题意知函数f(x)=loga(x+b)+c恒过定点(3,2),则2=loga(3+b) +c,
故3+b=1且c=2,
则b=-2,c=2,因此b+c=0.
答案:0(2)求函数f(x)=log2(x2+2x+9)的值域.规范解答:(2)因为x2+2x+9=(x+1)2+8≥8,……9分
且y=log2x在(0,+∞)上为增函数,
所以f(x)≥log28=3.……………………………11分
所以函数的值域为[3,+∞).……………………12分方法技巧(2)求对数型函数y=logaf(x)(a>0,且a≠1)的值域,需根据a的范围及f(x)的取值范围求解.(3)若函数f(x)=ln(x2+4x+t)的定义域、值域分别为R,求相应的t的范围.解:(3)由f(x)=ln(x2+4x+t)的定义域为R,知x2+4x+t>0恒成立,
所以Δ=16-4t<0,即t>4.
由f(x)=ln(x2+4x+t)的值域为R,知x2+4x+t应取遍所有正数,
所以Δ=16-4t≥0,即t≤4.题型五 易错辨析
[例5] 若函数f(x)=1-log2x,x∈[1,16],求y=[f(x)]2-f(x4)的值域.错解:因为f(x)=1-log2x,
所以y=[f(x)]2-f(x4)=(1-log2x)2-(1-log2x4)=(log2x)2+2log2x.
因为1≤x≤16,所以log21≤log2x≤log216,
所以0≤log2x≤4.
又y=(log2x+1)2-1,
所以当log2x=0,即x=1时,y有最小值0.
当log2x=4,即x=16时,y有最大值24.
故y=[f(x)]2-f(x4)的值域为[0,24].纠错:由于函数f(x)的定义域是[1,16],
因此f(x4)的定义域应满足1≤x4≤16,即1≤x≤2(x>0),
故错解过程忽视了函数y的定义域.
正解:因为f(x)的定义域为[1,16],
所以f(x4)的定义域满足1≤x4≤16,
即1≤x≤2,则0≤log2x≤1.
因为y=[f(x)]2-f(x4)=(1-log2x)2-(1-log2x4)=(log2x)2+2log2x=(log2x+1)2-1,
所以当log2x=0,即x=1时,f(x)有最小值0,
当log2x=1,即x=2时,f(x)有最大值3.
故y=[f(x)]2-f(x4)的值域为[0,3].学霸经验分享区(1)画对数函数图象时,要明确对数函数图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)形如y=loga(x+c)(a>0,且a≠1)的函数,可利用x+c=1时y=0确定函数图象所过定点的横坐标.
(3)求对数(或对数型)函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.课堂达标解析:设对数函数的解析式为y=logax(a>0,且a≠1),由于对数函数的图象过点M(16,4),所以4=loga16,解得a=2.所以对数函数的解析式为y=log2x,故选D.1.对数函数的图象过点M(16,4),则此对数函数的解析式为( )DC3.函数y=logax的图象如图所示,则实际a的可能取值是( )A解析:由x+2=1得x=-1,
故f(x)的图象过定点(-1,0).4.若函数f(x)=loga(x+2)(a>0,且a≠1),则不论a取何值,函数f(x)的图象恒过定点 .?答案:(-1,0)解析:因为2x>0,所以2x+3>3.
所以f(x)的值域即为反函数的定义域,是(3,+∞).5.若函数f(x)=2x+3,则其反函数的定义域是 .?答案:(3,+∞)
第一课时 对数函数的图象及性质[目标导航]新知导学·素养养成1.对数函数的概念
一般地,我们把函数 叫做对数函数,其中 是自变量,函数的定义域是 .y=logax(a>0,且a≠1)x(0,+∞) 2.对数函数的图象与性质(1,0)增减思考1:底数变化对对数函数图象形状有什么影响?对数函数的图象有什么特点?
答案:(1)对图象的影响:比较图象与y=1的交点,交点的横坐标越大,对应的对数函数的底数越大.也就是说,沿直线y=1由左向右看,底数a增大 (如图).3.反函数
对数函数y=logax(a>0,且a≠1)和指数函数y=ax(a>0,且a≠1)互为
.反函数思考2:同底数的指数、对数函数的定义域、值域有何关系?
答案:同底数的指数函数的定义域是同底数对数函数的值域,指数函数的值域是对数函数的定义域.
思考3:互为反函数的两个函数图象有何特征?
答案:关于直线y=x对称.名师点津(1)对数函数图象和性质的关系(2)若函数y=f(x)存在反函数,且点(a,b)在y=f(x)图象上,则点(b,a)必在其反函数图象上.课堂探究·素养提升题型一 对数函数的概念
[例1] (1)若函数y=log(2a-1)x+(a2-5a+4)是对数函数,则a= .答案:(1)4 答案:(2)2方法技巧(1)判断一个函数是对数函数必须是形如y=logax(a>0,且a≠1)的形式,即必须满足以下条件:
①系数为1;
②底数为大于0且不等于1的常数;
③对数的真数仅有自变量x.
(2)若已知对数函数过定点求解析式时,常用待定系数法,设f(x)= logax(a>0,且a≠1),将定点代入后利用指对数式互化或指数幂的运算性质求a.题型二 对数函数的图象特征
[例2] (1)已知函数y=loga(x+c)(a,c为常数,其中a>0,且a≠1)的图象如图,则下列结论成立的是( )
(A)a>0,c>1 (B)a>1,0
故0
法二 首先指数函数y=ax的图象只可能在上半平面,函数y=loga(-x)的图象只可能在左半平面,从而排除A,C;再看单调性,y=ax与y=loga (-x)的单调性正好相反,排除D.只有B中图象符合.故选B.(2)已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )方法技巧(1)y=ax与y=logax(a>0,且a≠1)互为反函数.
(2)若函数y=f(x)存在反函数,且y=f(x)过点(a,b),则其反函数过点(b,a).
(3)反函数的定义域是原函数的值域.[备用例3] 若函数f(x)=loga(x+b)+c(a>0,且a≠1)的反函数图象恒过定点(2,3),则b+c= .?解析:由题意知函数f(x)=loga(x+b)+c恒过定点(3,2),则2=loga(3+b) +c,
故3+b=1且c=2,
则b=-2,c=2,因此b+c=0.
答案:0(2)求函数f(x)=log2(x2+2x+9)的值域.规范解答:(2)因为x2+2x+9=(x+1)2+8≥8,……9分
且y=log2x在(0,+∞)上为增函数,
所以f(x)≥log28=3.……………………………11分
所以函数的值域为[3,+∞).……………………12分方法技巧(2)求对数型函数y=logaf(x)(a>0,且a≠1)的值域,需根据a的范围及f(x)的取值范围求解.(3)若函数f(x)=ln(x2+4x+t)的定义域、值域分别为R,求相应的t的范围.解:(3)由f(x)=ln(x2+4x+t)的定义域为R,知x2+4x+t>0恒成立,
所以Δ=16-4t<0,即t>4.
由f(x)=ln(x2+4x+t)的值域为R,知x2+4x+t应取遍所有正数,
所以Δ=16-4t≥0,即t≤4.题型五 易错辨析
[例5] 若函数f(x)=1-log2x,x∈[1,16],求y=[f(x)]2-f(x4)的值域.错解:因为f(x)=1-log2x,
所以y=[f(x)]2-f(x4)=(1-log2x)2-(1-log2x4)=(log2x)2+2log2x.
因为1≤x≤16,所以log21≤log2x≤log216,
所以0≤log2x≤4.
又y=(log2x+1)2-1,
所以当log2x=0,即x=1时,y有最小值0.
当log2x=4,即x=16时,y有最大值24.
故y=[f(x)]2-f(x4)的值域为[0,24].纠错:由于函数f(x)的定义域是[1,16],
因此f(x4)的定义域应满足1≤x4≤16,即1≤x≤2(x>0),
故错解过程忽视了函数y的定义域.
正解:因为f(x)的定义域为[1,16],
所以f(x4)的定义域满足1≤x4≤16,
即1≤x≤2,则0≤log2x≤1.
因为y=[f(x)]2-f(x4)=(1-log2x)2-(1-log2x4)=(log2x)2+2log2x=(log2x+1)2-1,
所以当log2x=0,即x=1时,f(x)有最小值0,
当log2x=1,即x=2时,f(x)有最大值3.
故y=[f(x)]2-f(x4)的值域为[0,3].学霸经验分享区(1)画对数函数图象时,要明确对数函数图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)形如y=loga(x+c)(a>0,且a≠1)的函数,可利用x+c=1时y=0确定函数图象所过定点的横坐标.
(3)求对数(或对数型)函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.课堂达标解析:设对数函数的解析式为y=logax(a>0,且a≠1),由于对数函数的图象过点M(16,4),所以4=loga16,解得a=2.所以对数函数的解析式为y=log2x,故选D.1.对数函数的图象过点M(16,4),则此对数函数的解析式为( )DC3.函数y=logax的图象如图所示,则实际a的可能取值是( )A解析:由x+2=1得x=-1,
故f(x)的图象过定点(-1,0).4.若函数f(x)=loga(x+2)(a>0,且a≠1),则不论a取何值,函数f(x)的图象恒过定点 .?答案:(-1,0)解析:因为2x>0,所以2x+3>3.
所以f(x)的值域即为反函数的定义域,是(3,+∞).5.若函数f(x)=2x+3,则其反函数的定义域是 .?答案:(3,+∞)
